Come la spirale di Archimede, anche la curva di Ippia può essere definita a partire da movimenti dinamici di oggetti geometrici. La spirale di Archimede si ottiene considerando un punto A che percorre una retta con velocità v mentre questa retta ruota attorno un punto.
Per definire la curva di Ippia si deve prendere in considerazione il seguente grafico:
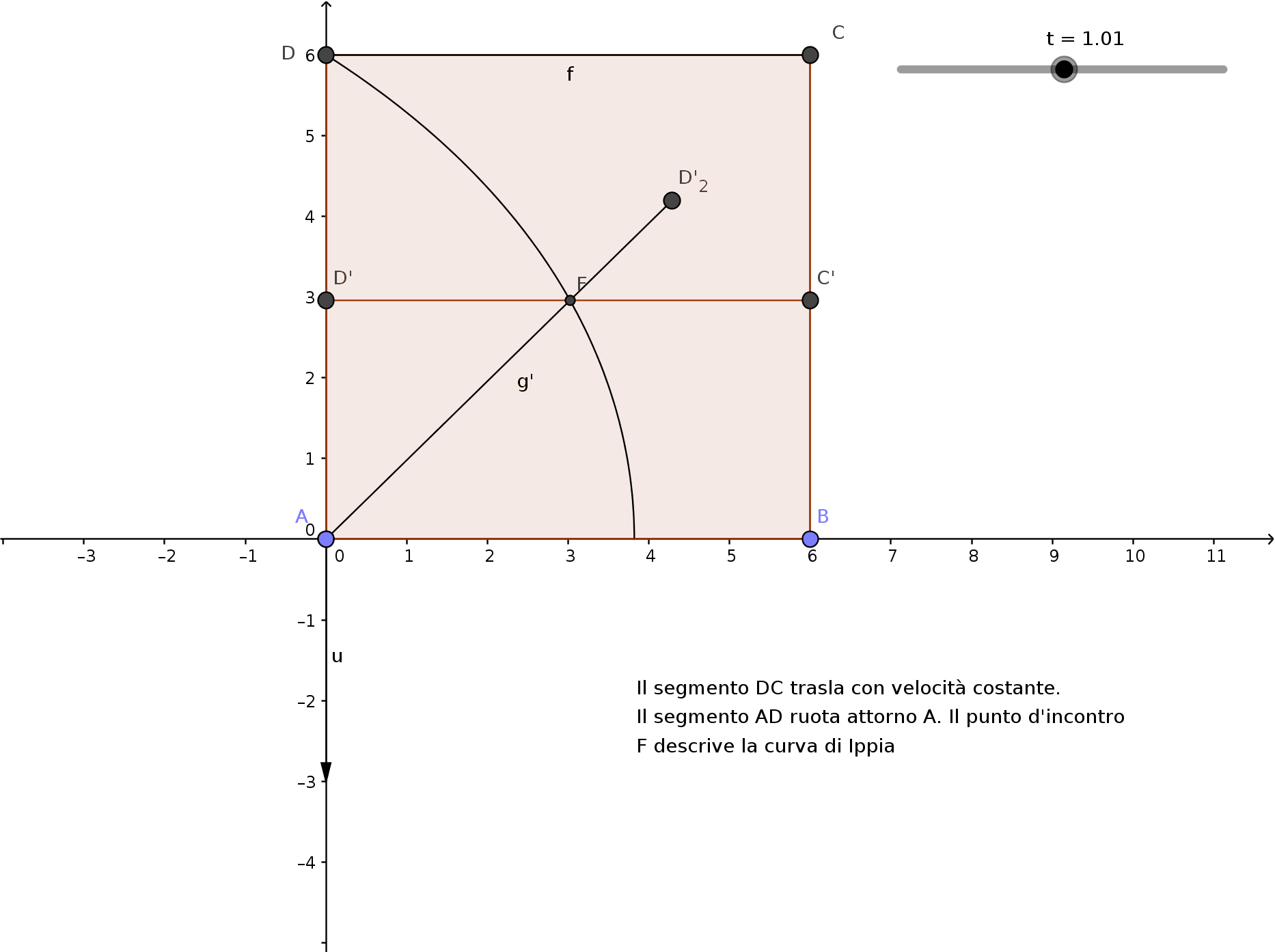
Supponiamo che il lato DC del quadrato trasli scendendo con una velocità v costante fino a sovrapporsi al lato AB. Contemporaneamente, il lato AD del quadrato ruoti attorno A con velocità angolare costante fino a sovrapporsi ad AB. Entrambi i movimenti avvengano nello stesso periodo T.
Il punto di incontro F fra i due segmenti in movimento, descrive la quadratrice di Ippia.
Volendo disegnare la curva di Ippia con GeoGebra, si può partire dal definire una variabile tempo t (con relativo cursore o slider), una variabile periodo T (maiuscolo e minuscolo sono variabili diverse) e la lunghezza L del quadrato.
Queste definizioni ci permettono di trovare la velocità v=L/T con cui scende il lato DC. Tenendo conto che l'angolo totale di cui ruota AD è dato da π/2 e il tempo totale è dato da T, la velocità angolare sarà ω=π/(2 T).
Queste formule vanno riscritte nella riga di comando di GeoGebra
Si tratta adesso di trovare le coordinate del punto F.
L'ordinata è facile da trovare:
n=L-v.t
L'angolo DAF di cui ruota il lato AD è dato da ω·t.
Guardando la figura seguente:
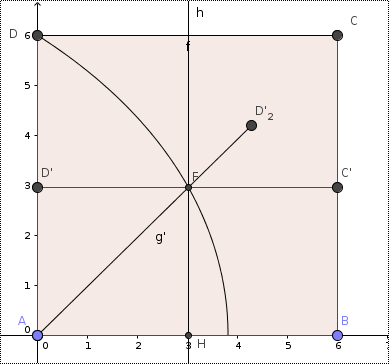
si trova che l'angolo DAF è uguale a AFH ed FH è proprio l'ordinata di F.
L'ascissa di F è il cateto AH. Esso è uguale all'altro cateto FH per la tangente trigonometrica dell'angolo opposto AFH e cioé ω·t
m=(L-v·t)·tg(ω·t)
A questo punto si possono definire nel GeoGebra due variabili m ed n trascrivendo le relazioni riportate prima ed anche il punto F
F=(m,n)
Si può definire in GeoGebra la curva di Ippia come curva parametrica:
Curva((L-v t) tg(ω .t), L-v t , t, 0,T)
Il parametro è t che varia fra 0 e T.
Bisogna osservare che effettivamente t non può diventare uguale a T perchè in questo caso la tangente tenderebbe all'infinito !
Per simulare la costruzione della curva è possibile rappresentare la traslazione verso l'asse x del lato DC. Basta definire un vettore u che abbia componenti zero come x e -v·t come y:
u=(0,-v·t)
Al variare di t, varierà il modulo del vettore traslazione.
Per far ruotare il lato AD del quadrato iniziale attorno il centro A è sufficiente ricordare che l'angolo è dato da ω·t in senso orario.
Come dividere un angolo in tre parti uguali
Sia dato l'angolo AFH da dividere in tre parti uguali.
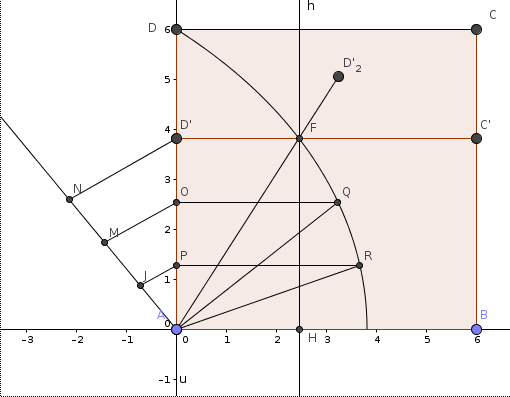
Si trova il segmento AD' che dovrà essere diviso facilmente in tre parti uguali. Dagli estremi dei tre segmenti in cui è stato diviso AD', si tracciano le parallele all'asse x e si individuano le intersezioni di queste parallele con la curva di Ippia definita come curva parametrica. Congiungendo A con questi punti di intersezione si individuano i tre angoli uguali.
L'uguaglianza deriva dalla definizione stessa di curva di Ippia. Infatti ad esempio gli angoli FAQ e QAR sono uguali perché ad una discesa di distanze uguali del lato DC corrisponderà una rotazione di angoli uguali del lato AD.
La curva di Ippia come quadratrice
Fino a questo punto ci si è avvalsi solo di un pochino di trigonometria; nel seguito invece saranno utilizzati i limiti di funzione per dimostrare come la curva di Ippia permetta di trovare un quadrato equivalente ad un cerchio.
Riprendiamo la definizione di ordinata di F punto della curva di Ippia e sostituiamo a v la sua definizione:
y= L-v·t=L-t·L/T=L·(1-t/T)
1-t/T=y/L
t/T=1-y/L
Ci serve esprimere diversamente l'angolo:
ω·t=t·π/(2·T)=π/2·t/T=π/2·(1-y/L)
Questa relazione ci permette di scrivere l'ascissa x del punto F della curva:
x=(L-v·t) tg(ω·t)=y·tg[π/2·(1-y/L)]
Questa è la relazione cartesiana fra x e y nella curva di Ippia.
Il limite per y che tende a zero ci fornisce l'ascissa del punto d'incontro della curva con l'asse x. Questo limite però si presenta nella forma indeterminata zero per infinito e lo si può calcolare col teorema di DeL'Hopital (anche utilizzando i calcoli simbolici o CAS di GeoGebra).
ascissa del punto di incontro con l'asse x= 2·L/π
Questa ascissa nella figura seguente è data da AJ.
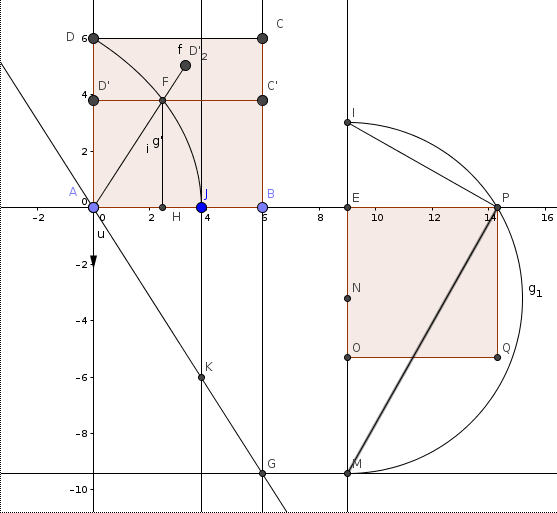
Per costruire il quadrato equivalente al cerchio di diametro L che è la lunghezza di AB, è necessario disegnare il segmento JK di lunghezza L perpendicolare ad AB. Si tracci la retta per AK e sia G il punto di incontro di essa con la perpendicolare per B all'asse x.
Utilizzando la similitudine dei triangoli, si trova BG:
BG=L·π/2
Si costruisca il segmento BE prolungamento di AB e di lunghezza L/2.
Il rettangolo BGME ha l'area del cerchio di diametro L.
Si disegni in fine il segmento EI prolungamento di ME e di lunghezza L/2. Il segmento IM si può pensare come il diametro di una semicirconferenza in cui l'altezza del triangolo rettangolo inscritto EP è il lato del quadrato equivalente al cerchio di diametro L.