






 |
 |
 |
 |
 |
 |
 |
Come nel caso delle altre liste linkate, un albero è costituito di nodi. Un tipo comune di albero è l' albero binario nel quale ciascun nodo fa riferimento a due altri nodi che possono anche avere valore None (in questo caso è prassi comune non indicarli nei diagrammi di stato). Questi riferimenti vengono normalmente chiamati "rami" (o "sottoalberi") sinistro e destro.
Come nel caso dei nodi degli altri tipi di lista anche in questo caso un nodo possiede un contenuto. Ecco un diagramma di stato per un albero:
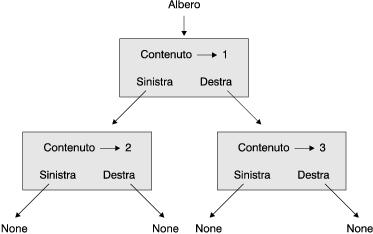
Il nodo principale dell'albero è chiamato radice, gli altri nodi rami e quelli terminali foglie. Si noti come l'albero viene generalmente disegnato capovolto, con la radice in alto e le foglie in basso.
Per rendere le cose più confuse vengono talvolta usate delle terminologie alternative che fanno riferimento ad un albero genealogico o alla geometria. Nel primo caso il nodo alla sommità è detto genitore e i nodi cui esso si riferisce figli; nodi con gli stessi genitori sono detti fratelli. Nel secondo caso parliamo di nodi a "sinistra" e "destra", in "alto" (verso il genitore/radice) e in "basso" (verso i figli/foglie).
Indipendentemente dai termini usati tutti i nodi che hanno la stessa distanza dalla radice appartengono allo stesso livello.
Come nel caso delle liste linkate gli alberi sono strutture di dati ricorsive:
Un albero è:
- un albero vuoto, rappresentato da None oppure
- un nodo che contiene un riferimento ad un oggetto e due riferimenti ad alberi.
Il processo di costruzione degli alberi è simile a quello che abbiamo già visto nel caso delle liste linkate. Ogni invocazione del costruttore aggiunge un singolo nodo:
class Albero:
def __init__(self, Contenuto, Sinistra=None, Destra=None):
self.Contenuto = Contenuto
self.Sinistra = Sinistra
self.Destra = Destra
def __str__(self):
return str(self.Contenuto)
Il Contenuto può essere di tipo qualsiasi ma sia Sinistra che Destra devono essere nodi di un albero. Sinistra e Destra sono opzionali ed il loro valore di default è None, significando con questo che non sono linkati ad altri nodi.
Come per gli altri nodi che abbiamo visto precedentemente, la stampa di un nodo dell'albero mostra soltanto il contenuto del nodo stesso.
Un modo per costruire un albero è quello di partire dal basso verso l'alto, allocando per primi i nodi figli:
FiglioSinistra = Albero(2)
FiglioDestra = Albero(3)
Poi creiamo il nodo genitore collegandolo ai figli:
Albero = Albero(1, FiglioSinistra, FiglioDestra);
Possiamo anche scrivere in modo più conciso questo codice invocando un costruttore annidato:
>>> Albero = Albero(1, Albero(2), Albero(3))
In ogni caso il risultato è l'albero presentato graficamente all'inizio del capitolo.
Ogni volta che vedi una nuova struttura la tua prima domanda dovrebbe essere "come posso attraversarla?". Il modo più intuitivo per attraversare un albero è quello di usare un algoritmo ricorsivo.
Per fare un esempio, se il nostro albero contiene interi questa funzione ne restituisce la somma:
def Totale(Albero):
if Albero == None: return 0
return Albero.Contenuto + Totale(Albero.Sinistra) + \
Totale(Albero.Destra)
Il caso base è l'albero vuoto che non ha contenuto e che quindi ha valore 0. Il passo successivo chiama due funzioni ricorsive per calcolare la somma dei rami figli. Quando la serie di chiamate ricorsiva è completa la funzione ritorna il totale.
Un albero è un modo naturale per rappresentare una struttura di espressioni e a differenza di altre notazioni può rappresentare la loro elaborazione in modo non ambiguo (l'espressione infissa 1 + 2 * 3 è ambigua a meno che non si sappia che la moltiplicazione deve essere elaborata prima dell'addizione).
Ecco l'albero che rappresenta questa espressione:
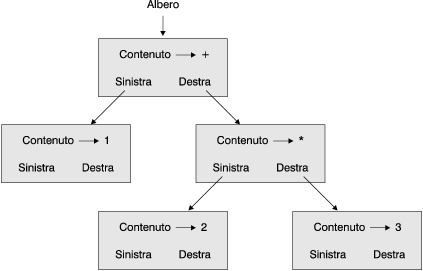
I nodi dell'albero possono essere operandi come 1 e 2 o operatori come + e *. Gli operandi sono i nodi foglia, e i nodi operatore contengono i riferimenti ai rispettivi operandi. È importante notare che tutte queste operazioni sono binarie nel senso che hanno esattamente due operandi.
Possiamo costruire alberi come questo:
>>> Albero = Albero('+', Albero(1), Albero('*', Albero(2), \
Albero(3)))
Guardando la figura non c'è assolutamente alcun problema nel determinare l'ordine delle operazioni: la moltiplicazione deve essere eseguita per prima per ottenere un risultato necessario all'addizione.
Gli alberi di espressioni hanno molti usi tra i quali possiamo citare la rappresentazione di espressioni matematiche postfisse e infisse (come abbiamo appena visto), e le operazioni di parsing, ottimizzazione e traduzione dei programmi nei compilatori.
Potremmo attraversare un espressione ad albero e stampare il suo contenuto con:
def StampaAlberoPre(Albero):
if Albero == None: return
print Albero.Contenuto,
StampaAlberoPre(Albero.Sinistra)
StampaAlberoPre(Albero.Destra)
Per stampare questo albero abbiamo deciso di stamparne la radice, poi l'intero ramo di sinistra e poi quello di destra. Questo modo di attraversare l'albero è detto con preordine perché la radice appare sempre prima del contenuto dei figli. La stampa nel nostro caso è:
>>> Albero = Albero('+', Albero(1), Albero('*', Albero(2), \
Albero(3)))
>>> StampaAlberoPre(Albero)
+ 1 * 2 3
Questo formato di stampa è diverso sia da quello che ci saremmo aspettati dalla notazione postfissa sia da quella infissa: si tratta infatti di una notazione chiamata prefissa nella quale gli operatori compaiono prima dei loro operandi.
Avrai già capito che cambiando l'ordine di attraversamento dell'albero sarà possibile ricavare le altre notazioni equivalenti. Se stampiamo prima i rami e poi il nodo radice otteniamo:
def StampaAlberoPost(Albero):
if Albero == None: return
StampaAlberoPost(Albero.Sinistra)
StampaAlberoPost(Albero.Destra)
print Albero.Contenuto,
Il risultato è 1 2 3 * + in notazione postfissa. Questo tipo di attraversamento è chiamato postordine.
L'ultimo caso da considerare è l'attraversamento dell'albero con inordine, dove stampiamo il ramo sinistro, poi la radice ed infine il ramo destro:
def StampaAlberoIn(Albero):
if Albero == None: return
StampaAlberoIn(Albero.Sinistra)
print Albero.Contenuto,
StampaAlberoIn(Albero.Destra)
Il risultato è 1 + 2 * 3 in notazione infissa.
Ad essere onesti dovremmo menzionare una complicazione molto importante sulla quale abbiamo sorvolato. Talvolta è necessario l'uso delle parentesi per conservare l'ordine delle operazioni nelle espressioni infisse, così che un attraversamento con inordine non è sufficiente a generare un'espressione infissa corretta.
Ciononostante, e con poche modifiche, l'albero delle espressioni e tre diversi attraversamenti ricorsivi ci hanno permesso di tradurre diverse espressioni da una notazione all'altra.
Esercizio: modifica StampaAlberoIn così da mettere un paio di parentesi che racchiuda ogni coppia di operandi ed il loro operatore. Il risultato può essere considerato a questo punto corretto e non ambiguo? Sono sempre necessarie le parentesi?
Se attraversiamo con inordine e teniamo traccia di quale livello dell'albero ci troviamo possiamo generare una rappresentazione grafica dell'albero:
def StampaAlberoIndentato(Albero, Livello=0):
if Albero == None: return
StampaAlberoIndentato(Albero.Destra, Livello+1)
print ' '*Livello + str(Albero.Contenuto)
StampaAlberoIndentato(Albero.Sinistra, Livello+1)
Il parametro Livello tiene traccia di dove ci troviamo nell'albero e per default vale inizialmente 0. Ogni volta che effettuiamo una chiamata ricorsiva passiamo Livello+1 perché il livello del figlio è sempre più grande di 1 rispetto a quello del genitore. Ogni elemento è indentato di due spazi per ogni livello.
Il risultato del nostro albero di esempio è:
>>> StampaAlberoIndentato(Albero)
3
*
2
+
1
Guardando la figura dopo aver girato il foglio vedrai una versione semplificata della figura originale.
In questa sezione effettueremo il parsing di un'espressione infissa e costruiremo il corrispondente albero. L'espressione (3+7)*9 produce questo diagramma, dove non sono stati indicati i nomi degli attributi:

Il parser che scriveremo dovrà riuscire a gestire espressioni contenenti numeri, parentesi e gli operatori + e *. Partiamo dal presupposto che la stringa da analizzare sia già stata spezzata in token che nel nostro caso sono elementi di una lista:
['(', 3, '+', 7, ')', '*', 9, 'end']
Il token end è stato aggiunto per fare il modo che il parser non continui la lettura al termine della lista.
Esercizio: scrivi una funzione che accetta un'espressione e la converte in una lista di token.
La prima funzione che scriveremo è ControllaToken che prende come parametri una lista di token e un token atteso: dopo aver confrontato il token atteso con il primo elemento della lista, se i due coincidono l'elemento della lista viene rimosso e viene ritornato il valore vero; in caso contrario viene ritornato falso.
def ControllaToken(ListaToken, TokenAtteso):
if ListaToken[0] == TokenAtteso:
del ListaToken[0]
return 1
else:
return 0
Dato che ListaToken si riferisce ad un oggetto mutabile i cambiamenti fatti sono visibili da qualsiasi altra variabile che si riferisce allo stesso oggetto.
La prossima funzione, ControllaNumero, gestisce gli operandi: se il prossimo elemento in ListaToken è un numero ControllaNumero lo rimuove dalla lista e ritorna un nodo foglia contenente il numero; in caso contrario viene ritornato None:
def ControllaNumero(ListaToken):
x = ListaToken[0]
if type(x) != type(0): return None
del ListaToken[0]
return Albero(x, None, None)
Prima di continuare è buona cosa testare isolatamente ControllaNumero. Assegniamo una lista di numeri a ListaToken, ne estraiamo il primo, stampiamo il risultato e ciò che rimane della lista di token:
>>> Lista = [9, 11, 'end']
>>> x = ControllaNumero(Lista)
>>> StampaAlberoPost(x)
9
>>> print Lista
[11, 'end']
Il prossimo metodo di cui avremo bisogno è EsprProdotto che costruisce un albero di espressione per le moltiplicazioni del tipo 3*7.
Ecco una versione di EsprProdotto che gestisce prodotti semplici:
def EsprProdotto(ListaToken):
a = ControllaNumero(ListaToken)
if ControllaToken(ListaToken, '*'):
b = ControllaNumero(ListaToken)
return Albero('*', a, b)
else:
return a
Se ControllaNumero ha successo e ritorna un nodo assegniamo il primo operando ad a. Se il carattere successivo è * ricaviamo il secondo numero e costruiamo un albero con a, b e l'operatore moltiplicazione. Se il secondo carattere è qualcos'altro ritorniamo il nodo foglia con contenuto pari ad a.
Ecco un paio di esempi:
>>> ListaToken = [9, '*', 11, 'end']
>>> Albero = EsprProdotto(ListaToken)
>>> StampaAlberoPost(Albero)
9 11 *
>>> ListaToken = [9, '+', 11, 'end']
>>> Albero = EsprProdotto(ListaToken)
>>> StampaAlberoPost(Albero)
9
Il secondo esempio mostra che noi consideriamo un singolo operando come una moltiplicazione valida. Questa definizione di "prodotto" non è proprio intuitiva, ma risulta esserci molto utile in questo caso.
Ora vediamo di gestire i prodotti composti, come in 3*5*13. Tratteremo questa espressione come prodotto di prodotti, e cioè 3*(5*13). L'albero risultante è:

Con un piccolo cambiamento in EsprProdotto possiamo gestire prodotti arbitrariamente lunghi:
def EsprProdotto(ListaToken):
a = ControllaNumero(ListaToken)
if ControllaToken(ListaToken, '*'):
b = EsprProdotto(ListaToken) # questa linea e' cambiata
return Albero('*', a, b)
else:
return a
In altre parole un prodotto può essere o un valore singolo o un albero con * alla radice, un numero a sinistra e un prodotto alla destra. Ormai dovresti cominciare a sentirti a tuo agio con questa definizione ricorsiva.
Testiamo la nuova versione con un prodotto composto:
>>> ListaToken = [2, '*', 3, '*', 5 , '*', 7, 'end']
>>> Albero = EsprProdotto(ListaToken)
>>> StampaAlberoPost(Albero)
2 3 5 7 * * *
Continuiamo con la nostra implementazione andando a gestire le somme. Ancora una volta useremo una definizione di somma che non è del tutto intuitiva: una somma può essere un albero con + alla radice, un prodotto a sinistra e una somma a destra. Inoltre consideriamo come "somma" anche un prodotto.
Se non riesci a comprenderne il significato, è possibile immaginare qualsiasi espressione priva di parentesi (ricorda che stiamo lavorando solo su addizioni e moltiplicazioni) come somme di prodotti. Questa proprietà rappresenta la base del nostro algoritmo di parsing.
EsprSomma prova a costruire un albero con un prodotto a sinistra e una somma a destra; nel caso non riesca a trovare un operatore + restituisce il prodotto.
def EsprSomma(ListaToken):
a = EsprProdotto(ListaToken)
if ControllaToken(ListaToken, '+'):
b = EsprSomma(ListaToken)
return Albero('+', a, b)
else:
return a
Proviamo con 9 * 11 + 5 * 7:
>>> ListaToken = [9, '*', 11, '+', 5, '*', 7, 'end']
>>> Albero = EsprSomma(ListaToken)
>>> StampaAlberoPost(Albero)
9 11 * 5 7 * +
Ora ci mancano solo le parentesi. Dovunque in un'espressione compaia un numero, lì può essere racchiusa un'intera somma tra parentesi. Dobbiamo solo modificare ControllaNumero per gestire le sub-espressioni:
def ControllaNumero(ListaToken):
if ControllaToken(ListaToken, '('):
x = EsprSomma(ListaToken) # ricava la sub-espressione
ControllaToken(ListaToken, ')') # rimuove la parentesi
# chiusa
return x
else:
x = ListaToken[0]
if type(x) != type(0): return None
ListaToken[0:1] = []
return Albero(x, None, None)
Testiamo questa nuova funzione con 9 * (11 + 5) * 7:
>>> ListaToken = [9, '*', '(', 11, '+', 5, ')', '*', 7, 'end']
>>> Albero = EsprSomma(ListaToken)
>>> StampaAlberoPost(Albero)
9 11 5 + 7 * *
Il parser ha gestito correttamente le parentesi e l'addizione viene eseguita prima della moltiplicazione.
Nella versione finale del programma è una buona idea dare a ControllaNumero un nuovo nome più coerente con il suo nuovo ruolo.
Le espressioni che dobbiamo passare al parser devono essere ben formate. Se abbiamo raggiunto la fine di una sub-espressione ci aspettiamo una parentesi chiusa: nel caso questa non sia presente sarebbe il caso di gestire questa condizione d'errore.
def ControllaNumero(ListaToken):
if ControllaToken(ListaToken, '('):
x = EsprSomma(ListaToken)
if not ControllaToken(ListaToken, ')'):
raise 'BadExpressionError', 'manca la parentesi'
return x
else:
# omettiamo il resto della funzione
L'istruzione raise crea un'eccezione: in questo caso abbiamo creato un nuovo tipo di errore chiamato BadExpressionError. Se la funzione che chiama ControllaNumero o una delle altre funzioni indicate in traccia al momento dell'errore gestisce le eccezioni allora il programma può continuare; in caso contrario Python mostra il messaggio di errore e si interrompe.
Esercizio: trova altri posti in queste funzioni in cui possono verificarsi errori e aggiungi le istruzioni raise appropriate. Testa successivamente il tuo codice passando alle funzioni delle espressioni errate.
In questa sezione svilupperemo un piccolo programma che usa un albero per rappresentare un sistema di conoscenze e aumentando la sua ampiezza grazie all'interazione con l'operatore.
Il programma interagisce con l'operatore per creare un albero di domande e di nomi di animali. Ecco un esempio del suo funzionamento:
Stai pensando ad un animale? s
E' un uccello? n
Qual e' il nome dell'animale? cane
Che domanda permette di distinguere tra un cane e un \
uccello? Puo' volare
Se l'animale fosse un cane quale sarebbe la risposta? n
Stai pensando ad un animale? s
Puo' volare? n
E' un cane? n
Qual e' il nome dell'animale? gatto
Che domanda permette di distinguere tra un gatto e un\
cane? Abbaia
Se l'animale fosse un gatto quale sarebbe la risposta? n
Stai pensando ad un animale? s
Puo' volare? n
Abbaia? s
E' un cane? s
Ho indovinato!
Stai pensando ad un animale? n
Ecco un albero costruito da questo dialogo:
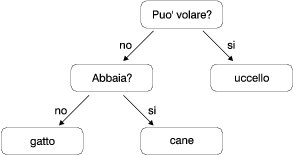
All'inizio di ogni round il programma parte alla radice dell'albero e pone la prima domanda. A seconda della risposta si muove a destra o a sinistra lungo l'albero e continua fino a raggiungere una foglia. A questo punto tira a indovinare: se la sua ipotesi non è corretta chiede il nome dell'animale pensato dall'operatore e una domanda per poterlo distinguere dall'animale trovato nel nodo foglia. Poi aggiunge il nuovo animale come nodo all'albero, assieme alla nuova domanda.
Ecco il codice:
def Animale():
# parte con una lista composta di un solo elemento
Radice = Albero("uccello")
# continua finche' l'operatore non abbandona
while 1:
print
if not RispostaAffermativa("Stai pensando ad un \
animale? "): break
# percorre l'albero
SottoAlbero = Radice
while SottoAlbero.RamoSinistro() != None:
Messaggio = SottoAlbero.OttieniContenuto() + "? "
if RispostaAffermativa(Messaggio):
SottoAlbero = SottoAlbero.RamoDestro()
else:
SottoAlbero = SottoAlbero.RamoSinistro()
# prova a indovinare
Ipotesi = SottoAlbero.OttieniContenuto()
Messaggio = "E' un " + Ipotesi + "? "
if RispostaAffermativa(Messaggio):
print "Ho indovinato!"
continue
# ottiene nuove informazioni
Messaggio = "Qual e' il nome dell'animale? "
Animale = raw_input(Messaggio)
Messaggio = "Che domanda permette di distinguere tra \
un %s e un %s? "
Domanda = raw_input(Messaggio % (Animale, Ipotesi))
# aggiunge le nuove informazioni all'albero
SottoAlbero.SettaContenuto(Domanda)
Messaggio = "Se l'animale fosse un %s quale sarebbe la \
risposta? "
if RispostaAffermativa(Messaggio % Animale):
SottoAlbero.SettaRamoSinistro(Albero(Ipotesi))
SottoAlbero.SettaRamoDestro(Albero(Animale))
else:
SottoAlbero.SettaRamoSinistro(Albero(Animale))
SottoAlbero.SettaRamoDestro(Albero(Ipotesi))
La funzione RispostaAffermativa è solo un'aiutante e serve a stampare un messaggio attendendo la risposta dall'operatore. Se la risposta inizia con s o S la funzione ritorna vero:
def RispostaAffermativa(Domanda):
from string import lower
Risposta = lower(raw_input(Domanda))
return (Risposta[0] == 's')
La condizione del ciclo esterno è 1 e questo significa che il ciclo verrà eseguito finchè non si incontra un'istruzione break, nel caso l'operatore non stia pensando ad un animale.
Il ciclo while interno serve a percorrere l'albero dall'alto in basso, guidato dalle risposte dell'operatore.
Se dopo aver raggiunto un nodo foglia ci troviamo a dover inserire un nuovo animale (con la rispettiva domanda per distinguerlo da quello rappresentato dal nodo foglia), viene effettuata una serie di operazioni:
Un "piccolo" problema con questo programma è che non appena termina la sua esecuzione tutto quello che gli abbiamo insegnato viene dimenticato...
Esercizio: pensa ai vari modi in cui potresti salvare l'albero su file e poi implementa quello che ritieni sia il più semplice.
 |
 |
 |
 |
 |
 |
 |