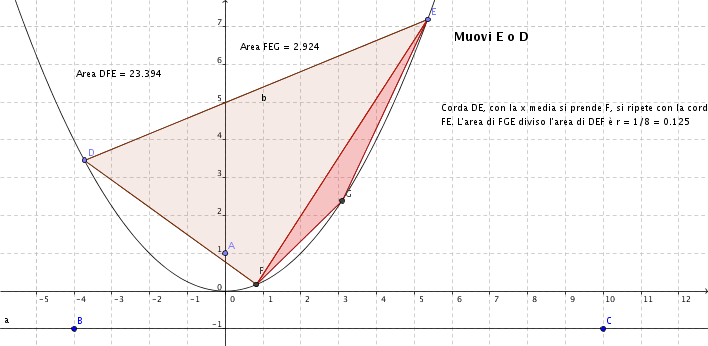
Quadratura della parabola con il metodo di Archimede

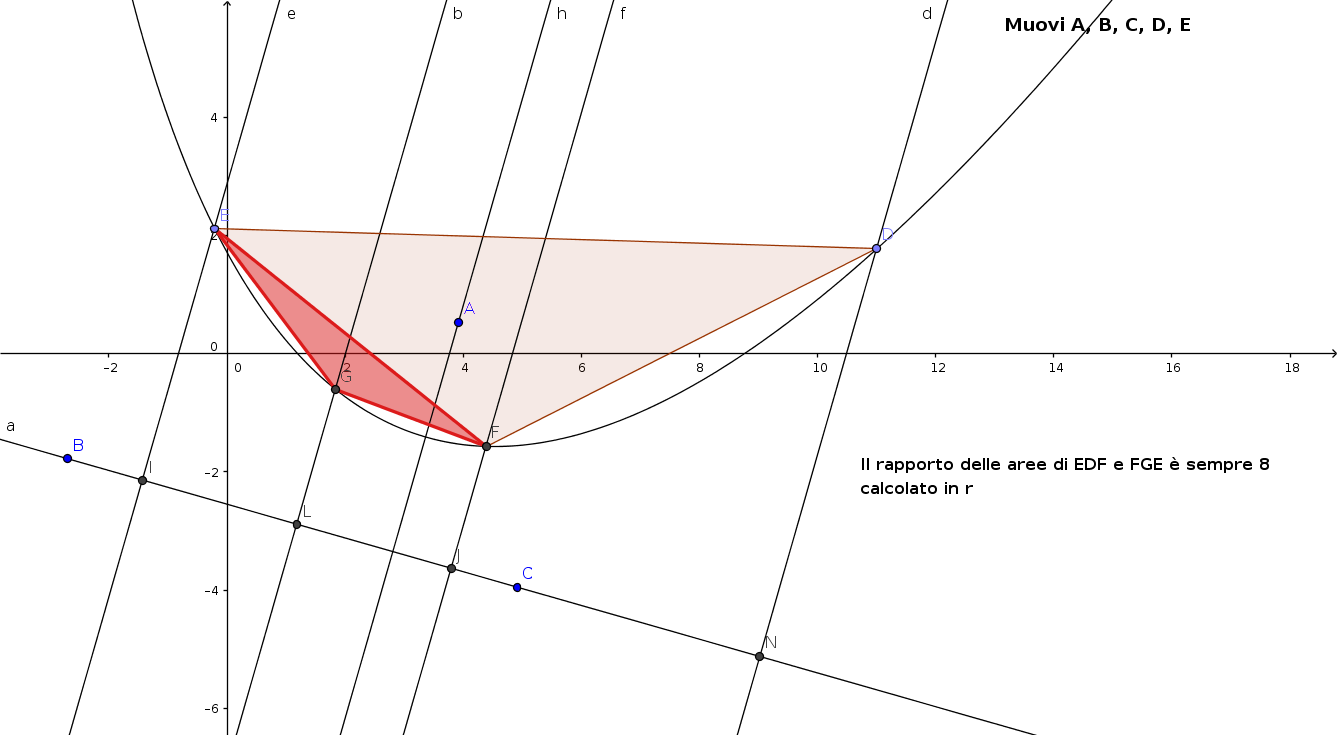
Data una qualunque parabola con asse parallelo all'asse y, sia DE una corda (che individua un segmento parabolico). Si prenda F tale xF=(xD+xE)/2, sulla parabola. Il triangolo EDF è detto di Archimede.
Si ripete la costruzione con FE. Si ottiene il triangolo FGE. Si può dimostrare che l'area di FGE è un ottavo di EDF.
Una trattazione su Wikipedia è questa.
Un file creato con Geogebra per visualizzare o “verificare” questa proprietà dei triangoli di Archimede.
Per dimostrare questa proprietà almeno nel caso di una parabola di equazione y=x^2, si può procedere così:
Si indichino con a e b le ascisse dei punti D ed E. In questo modo si trovano in funzione di a e b le coordinate di D, E e F.
Si può trovare quindi l'area del triangolo EDF per esempio tracciando le parallele all'asse y passanti per ciascuno dei vertici del triangolo e considerando le aree dei tre trapezi che si vengono a costituire. Con alcuni passaggi si trova che l'area cercata è data dal valore assoluto di:
Area EDF= (b-a)3/8
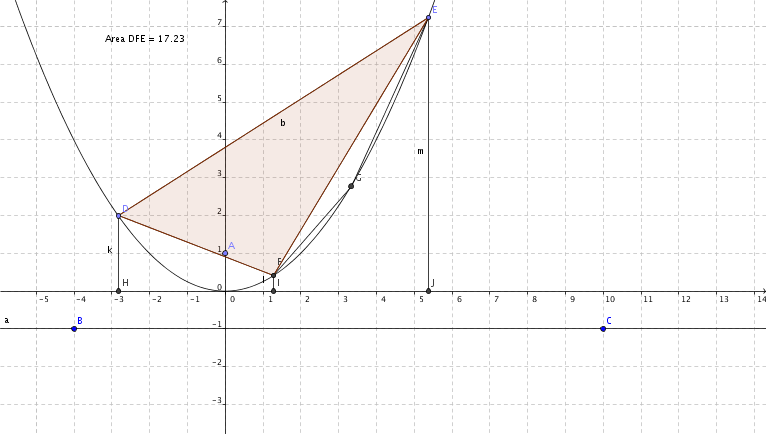
Nella figura tre trapezi rettangoli con i lati obliqui dati da ciascun lato del triangolo EDF.
Procedendo nello stesso modo per trovare l'area del triangolo EFG si ottiene:
Area EDF= (b-a)3/64
Quindi le aree dei due triangoli EDF e EFG stanno fra loro come 8 sta ad 1.
E' possibile anche fare ricorso alla formula che fornisce l'area di un triangolo a partire dalla matrice di ordine 3 X 3 con le prime due colonne date dalle coordinate dei vertici e l'ultima tutta di 1.
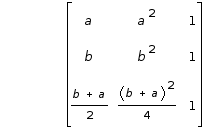
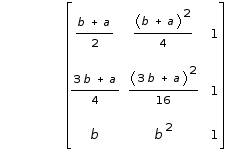
Per calcolare il determinante ci si può avvalere dell'aiuto di un programma per calcoli simbolici quale ad esempio wxMaxima in ambiente Linux.
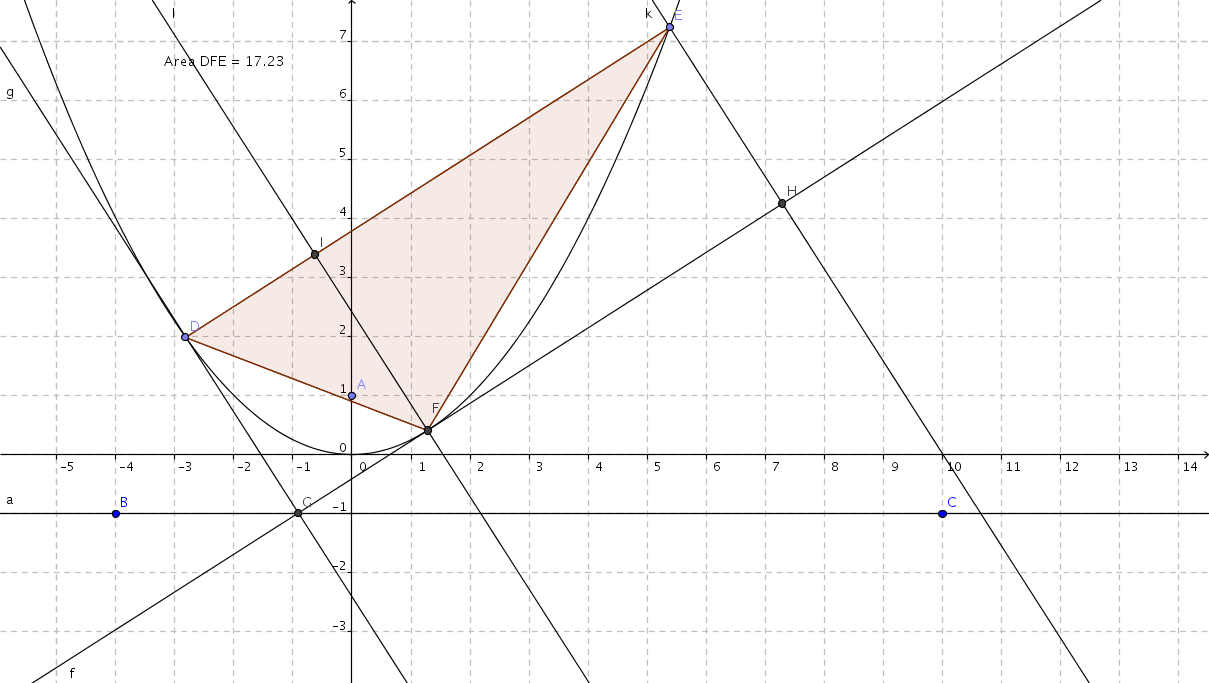
In effetti, nel caso in cui la parabola non abbia asse parallelo all'asse
y, si deve procedere in modo diverso per definire il triangolo di Archimede
(vedi anche il file
GeoGebra). A partire dalla corda DE, il terzo vertice F deve essere scelto in
modo tale che la parallela all'asse della parabola passate per F disti
ugualmente dalle parallele condotte sia da D che da E.
Per fare questo si può procedere così: si tracciano le perpendicolari alla direttrice della parabola condotte da D e da E e siano N ed I i piedi delle pependicolari. Si trova quindi il punto medio J fra N ed I. Da J si traccia la parallela all'asse della parabola e si trova il punto d'incontro con la parabola stessa che sarà F.
In ForMat Spe vol I pag. 997 di Maraschini e Palma si fa notare che “due parabole sono sempre simili” cioè si possono ottenere l'una dall'altra applicando una omotetia e una isometria. Partendo quindi dalla parabola y=x^2 si può ottenere una parabola di equazione y=k x^2 applicando l'omotetia di centro l'origine e rapporto 1/k. Con una successiva isometria si può fare corrispondere una qualunque altra parabola di concavità k.
Quando si applica una omotetia i rapporti delle aree di due triangoli rimangono invariate. Quindi in maniera generale il rapporto delle aree dei due triangoli di Archimede è dimostrato essere 8.
Indichiamo con T l'area di DEF. Dale corde DF e EF si originano due triangoli ciascuno di area 1/8 di quella di DEF. Il procediimento prosegue con le nuove corde FG e GE. Allora l'area del segmento parabolico sarà:
Sp= T+2 T/8+4 T/64+8 T/512+16 T/4096+...
Sp= T (1+1/4+1/16+1/64+1/256+... )
Serie geometrica di ragione q=1/4 e primo termine a1=1. Applicando la formula per la somma:
Somma=a1 (qn-1)/(q-1)
si ottiene:
Somma=((1/4)n-1)/(-3/4)
Facendo tendere n all'infinito, (1/4)n tende a zero e allora si ottiene:
Somma= 4/3
Quindi il segmento parabolico è 4/3 del triangolo di Archimede iniziale.
Sp= T 4/3
Consideriamo una corda di una parabola, la retta tangente alla parabola parallela alla corda, i due segmenti perpendicolari alla tangente condotti dagli estremi della corda.
Si può facilmente dimostrare che tale rettangolo ha area pari a 3/2 del segmento parabolico.
Per provarlo osserviamo che il rettangolo ha area il doppio del triangolo di Archimede. E allora:
Area rettangolo = 2 Area Triangolo= 2 3/4 Area Sp= 3/2 Area Sp
Cioè il rettangolo è 3/2 dell'area del segmento parabolico. In altri termini quest'ultimo è i 2/3 del rettangolo. Il rettangolo quindi è diviso dalla parabola in due parti di cui una è i 2/3 e l'altra 1/3 dell'area del rettangolo.
Con le derivate è facile dimostrare che l'ascissa del punto medio fra D ed E è un valore di x per cui la tangente alla parabola è parallela alla corda DE. Data l'equazione y=x^2 e indicati come prima con a la x di D e con b la x di E, basta calcolare il coefficiente angolare della corda DE e porlo uguale alla funzione derivata y'=2 x.