![]()
ha la caratteristica di avere il tasso di variazione costante per intervalli costanti della variabile indipendente x. In altre parole se si considera l'incremento della funzione diviso il suo valore iniziale, questo rapporto è costante ovviamente se si prende lo stesso intervallo per le x:
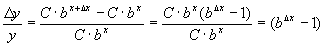
per D x costante, il rapporto non varia.
Allora si può dire che la variazione di y è proporzionale ad y. Tanto più grande è y tanto maggiore sarà la variazione, il rapporto però resta costante.
- - - - - - -
Funzioni che descrivono il decremento esponenziale
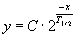
dove C rappresenta il valore iniziale e T1/2 il tempo di dimezzamento.
![]()
per il significato del coefficiente p vedi dopo.
Funzione esponenziale in base due e in base "numero di Nepero"
Una funzione esponenziale di crescita utilizzando la base due si può
scrivere:
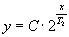
dove T2 rappresenta il tempo di raddoppio di y e C il valore di y al tempo x uguale a zero.
Vediamo in che modo debba essere scritta una funzione che rappresenti la stessa crescita esponenziale però in base il numero "e":
![]()
dove p è una costante da determinare per rendere questa funzione
di valore uguale a quella precedente.
Ponendo uguali le due y e passando ai logaritmi si ha:
![]()
Ovvero:
![]()
Per indagare meglio il significato di p, calcoliamo la variazione percentuale di y quando x varia di 1:
![]()
Ora esiste una formula approssimata per cui:
![]()
se p << 1 molto minore di 1 ovvero molto piccolo.
Concludendo p rappresenta il tasso di variazione percentuale nel caso in cui esso sia piccolo.