| Vernier Format 2 | ||||
| striscia_ottica.mbl | 11:09 Wednesday, November 14, 2001 | |||
| Latest | ||||
| Time | DeltaT | Distance | Velocity | Accel |
| T | DelT | Dist | V | A |
| s | s | m | m/s | m/s^2 |
|
0
|
0
|
|||
|
0,048
|
0,04841
|
0,050
|
1,270
|
9,778
|
|
0,083
|
0,03474
|
0,100
|
1,610
|
9,838
|
|
0,112
|
0,02856
|
0,150
|
1,891
|
9,788
|
|
0,137
|
0,02485
|
0,200
|
2,134
|
9,823
|
|
0,159
|
0,02228
|
0,250
|
2,352
|
9,749
|
|
0,179
|
0,02039
|
0,300
|
2,550
|
9,636
|
|
0,198
|
0,01893
|
0,350
|
||
Questa tabella si ottiene con il programma della Vernier predisposto per la caduta libera di una striscia ottica (bande nere alternate a bande trasparenti).
Lasciando semplicemente cadere la striscia, essa arriverà alla fotocellula con una velocità iniziale diversa da zero.
Come si può trovare la velocità per ciascun valore del tempo ?
Il valore di delta T si riferisce all'intervallino di tempo per percorrere 5 cm fissi.
E' quindi facile trovare la velocità media con cui vengono percorsi i successivi intervalli di spazio di 5 cm ciascuno.

Grafico delle velocità medie in ciascun intervallino di tempo delta T che risulta via via decrescente.
Volendo eseguire un grafico tempo-velocità, queste successive velocità medie come debbono essere riportate ? A quale tempo debbono essere riferite ?
La risposta è che debbono essere riferite al "tempo medio" ovvero all'istante che divide in due parti uguali ciascun intervallino delta T. Questi istanti possono essere calcolati applicando la formula del punto medio a ciascuna coppia successiva di valori nella prima colonna della tabella di sopra: (t1+t2)/2.
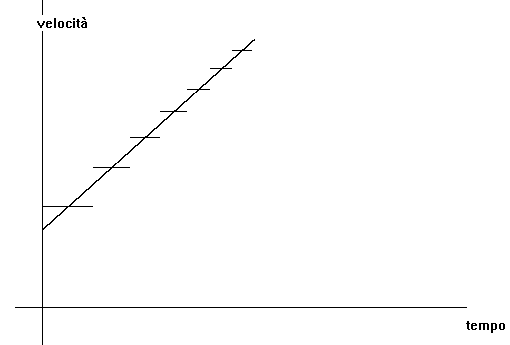
Retta della velocità al variare del tempo. Al tempo medio di
ogni intervallino corrisponde il valore medio della velocità.
| Time | tempo | v_media |
| T | medio | |
| s | s | m/s |
|
0
|
0
|
|
|
0,048
|
0,024
|
1,0329
|
|
0,083
|
0,066
|
1,4394
|
|
0,112
|
0,097
|
1,7508
|
|
0,137
|
0,124
|
2,0122
|
|
0,159
|
0,148
|
2,2437
|
|
0,179
|
0,169
|
2,4517
|
|
0,198
|
0,189
|
2,6412
|
Il tempo medio si trova aggiungendo il tempo successivo più il tempo precedente e dividendo per due. La velocità media si trova dividendo 0,05 per ciascun valore del delta T riportato prima.
Adesso si può eseguire il grafico tempo medio- velocità media
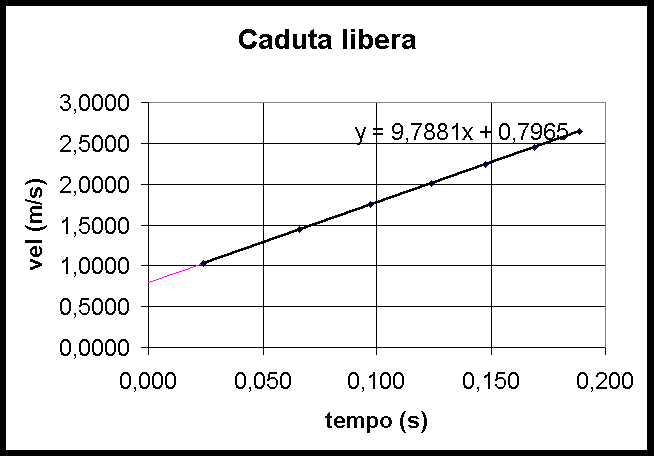
Con la retta di regressione si può sapere l'accelerazione ed anche la velocità media.
Altrimenti senza regressione lineare, si può calcolare
l'accelerazione come rapporto fra la variazione della velocità media
e il corrispondente intervallo di tempo.
| a |
| m/s^2 |
|
9,7784
|
|
9,8375
|
|
9,7885
|
|
9,8234
|
|
9,7491
|
|
9,6361
|
|
9,7954
|
L'ultimo è il valor medio dell'accelerazione.
Prendendo adesso una coppia di valori del tempo e della velocità si può calcolare la velocità iniziale. Con t=0,097 s ed v= 1,7508 m/s si ha:
v0=v-a t=0,7965 m/s
Con l'equazione:
v=0,7965+9,7954 t
si possono adesso calcolare i valori della velocità al variare del tempo.
----
Si poteva operare direttamente con il grafico tempo-spazio e con interpolazione quadratica.