Gli algebristi italiani nel corso del 1500 s’impegnarono nella risoluzione delle equazioni di terzo grado e nei loro sforzi dovettero iniziare ad immaginare un nuovo tipo di numero. Successivamente, a questi numeri verrà dato il nome di numeri complessi ed essi costituiscono un’estensione dei numeri reali.
Consideriamo un’equazione di terzo grado dopo aver diviso per il termine di grado massimo: x3 +ax2 +bx+c=0 a, b, c appartenenti ad R
Se effettuiamo la trasformazione x-> x-a/3, abbiamo:
ponendo:
si può scrivere:
x3 +px+q=0 p, q appartenenti ad R
Si può dimostrare che questa equazione ammette come formula risolutiva:
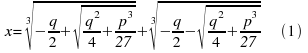
Si può far vedere che a volte capita che pur essendo:
la formula restituisce un valore reale che è soluzione della equazione di terzo grado. In altri termini nell’insieme dei numeri reali non esiste la radice di un numero negativo però esiste l’insieme dei numeri complessi dove questa radice esiste sempre ed operando con essi nella formula risolutiva si può trovare la soluzione reale esatta dell’equazione di terzo grado.
Con un esempio si chiariranno le idee. Sia data l’equazione di terzo grado:
x3 –15x+4 = 0 (2)
x3 –15x+4 = (x+4)(x2 –4x+1) = 0
x+4 = 0 x = -4
x2 –4x+1 = 0
Quindi l’equazione (2) ha tre soluzioni reali. Volendo utilizzare la formula (1) dopo alcuni calcoli si avrà:
Ci ritroviamo quindi con una radice quadrata di un numero negativo dentro un’espressione che deve per forza condurre ad un numero reale. Furono problemi di questo genere ad indurre i matematici ad introdurre un nuovo concetto di numero. Supponiamo di poter scrivere un numero nuovo indicato con la lettera i unità immaginaria tale che:
Con questa posizione si ottiene:
Osserviamo adesso che:
(-2+i) 3 = -2+11i ed anche (-2-i)3 = -2-11i
e quindi:
Abbiamo finalmente riottenuto la soluzione reale x=-4. In altri termini abbiamo considerato i nuovi numeri nella forma a + i b, operando con le solite “regole algebriche” e tenendo conto che i2 = -1, abbiamo ritrovato la soluzione reale –4.
Esercizio: ripetere l’esempio fatto con l’equazione: x3 –15x-4 = 0
Esercizio: applicare la formula risolutiva alla equazione x3 +6x-20 = 0
Suggerimento:
Consideriamo l’insieme di tutti i vettori del piano che escono dall’origine del riferimento cartesiano. Questi vettori possono essere considerati numeri di nuovo tipo: costituiscono l’insieme dei numeri complessi C. Ogni numero complesso può essere scritto come una coppia di numeri reali:
z=( x ; y )
dove x e y sono le coordinate della punta del vettore.
Tali coppie possono essere considerate numeri perché è possibile definire l’operazione di somma e di moltiplicazione.
l’operazione di addizione di due numeri complessi z1=(x1;y1) e z2=(x2;y2) è così definita: z1+z2= (x1;y1)+(x2;y2) = (x1+x2; y1+y2). Si tratta in sostanza della classica definizione di somma di due vettori nel piano con la regola del parallelogramma.
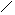
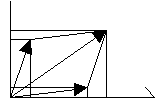
l’operazione di moltiplicazione di due numeri complessi z1=(x1;y1) e z2=(x2;y2) è così definita: z1 z2= (x1;y1)(x2;y2) = (x1x2-y1y2;y1x2+x1y2)
Rispetto l’addizione, l’insieme C forma un gruppo cioè valgono le stesse proprietà valide in R:
l’insieme è chiuso rispetto l’addizione ovvero la somma di due vettori è essa stessa un vettore
l’addizione è associativa [(a; b)+(c; d)]+(e; f) = (a; b)+[(c; d)+(e; f)]
il vettore nullo (0;0) è l’elemento neutro
esiste sempre l’inverso rispetto l’operazione di addizione (opposto): l’inverso di (x; y ) è (- x; -y)
Per quanto riguarda l’operazione di moltiplicazione che può apparire a prima vista astrusa, essa si può interpretare dal punto di vista geometrico nel seguente modo: moltiplicando due vettori se ne ottiene un terzo che ha per modulo il prodotto dei moduli e forma con l’asse delle x un angolo dato dalla somma dei due angoli che ciascun vettore forma con l’asse delle x.
Anche rispetto
l’operazione di moltiplicazione, l’insieme C è un gruppo:
l’insieme è chiuso rispetto la moltiplicazione; il prodotto di due vettori è ancora un vettore
la moltiplicazione è associativa
esiste l’elemento neutro (1;0). Infatti: (x; y) . (1;0) = (x; y)
ogni numero complesso diverso da zero possiede l’inverso: l’inverso di (a; b) sarà (c; d) in modo tale che (a; b) . (c; d) = (1; 0) quando:
Vale anche la distributiva della moltiplicazione rispetto all’addizione.
Infatti tutte le coppie del tipo (x; 0) identificano il numero reale x. Inoltre:
(x; 0) + (y; 0) = (x+y; 0) ed anche (x; 0) . (y; 0) = (x . y; 0).
L’insieme C contiene come sottoinsieme R. In C è sempre possibile l’operazione di radice quadrata di un numero reale negativo. Non è invece possibile definire un ordinamento dei numeri come si fa in R. Mentre tutti i numeri reali si possono rappresentare in una retta e quindi ordinarli, ciò non è possibile per i numeri complessi che possono essere rappresentati in un piano dove non è possibile stabilire un ordinamento. Il piano dei numeri complessi viene detto piano di Argand-Gauss ed ha l’unità immaginaria nell’asse delle ordinate.
In base a quanto detto il numero complesso (-1; 0) è uguale a –1.
Da notare in fine l’importanza fondamentale del numero complesso (0; 1). Per esso vale:
(0; 1) . (0; 1) = (-1; 0)
Il numero complesso (0; 1) si indica con la lettera i e quindi:
i2= (-1; 0) = -1
Un numero complesso del tipo (0; y) si può scrivere come prodotto dell’unità immaginaria i moltiplicata per (y; 0):
(0; y) = (0; 1) . (y; 0) = i (y; 0) = i . y
Inoltre ogni numero complesso (x; y) si può scrivere:
(x; y) = (x; 0) + (0; y) = x + i . y
Scrivendo i numeri complessi in questo modo, a + i . b, si può più facilmente operare su di essi con le solite regole algebriche con la particolarità che i2= -1 .
Due numeri complessi del tipo a + i . b e a - i . b vengono detti coniugati.
Volendo trovare l’asse di una parabola basta fare il punto medio fra i punti d’incontro della parabola con l’asse delle x.
Quando una parabola non ha punti d’incontro con l’asse delle x, allora il delta è minore di zero. In questo caso ponendo uguale a zero la y, si ottiene una equazione di secondo grado in x che ammette due soluzioni nell’insieme dei numeri complessi. Queste soluzioni sono complesse coniugate.
Anche in questo caso di soluzioni complesse è possibile trovare l’asse della parabola applicando la formula del punto medio ai numeri complessi.
Esempio
Verificare che l’asse della parabola y=x2 –4x+5 è x=2.
Applicando la formula risolutiva dell’equazione di secondo grado si ottiene:
x2 –4x+5=0; x=2 + - i
Come si ricava la formula risolutiva dell’equazione di terzo grado
Sostituiamo nella equazione x3 +px+q=0, x = u+v con la condizione:
u v = -p/3
Si ottiene:
u3 +v3 +(3uv+p)(u+v)+q =0
Con la condizione posta si semplifica e si ottiene:
u3 +v3 = -q
Ponendo a sistema questa equazione con quella ottenuta elevando al cubo la condizione posta prima (questo porta ad introdurre nuove soluzioni che non sono soluzioni della equazione iniziale), si ha:
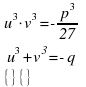
Sostituendo ad esempio u si ha:
Ponendo
adesso v3 = t, si ottiene l’equazione risolvente:
Applicando la formula
delle equazioni di secondo grado si ha:
Nello stesso identico modo si procede per trovare u. In conclusione si possono scegliere le soluzioni:
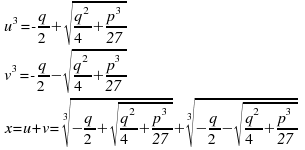
Teorema di Ruffini: Il valore che un polinomio a(x) assume sostituendo ad x il numero k appartenente ad R è uguale al resto della divisione di a (x) per il binomio x-k.
Infatti dividendo un polinomio a(x) per un polinomio b(x) si ottiene:
a(x) = b(x) q(x) + r(x)
Nel nostro caso sarà q(x) = (x-k) ed r una costante dovendo essere di grado inferiore ad uno e quindi zero:
a(x) = b(x) (x-k) + r
Calcolando a(x) per x=k, si ha:
a(k) = b(k) (k-k) + r = r
Conseguenza del teorema di Ruffini: un polinomio p(x) è divisibile per il binomio x-k se e solo se k è uno zero di a(x) cioè se e solo se a(k) = 0.
Teorema 2: Il prodotto di due binomi (x-z1) (x-z2) in cui z1 e z2 sono numeri complessi non reali, ha coefficienti reali se e solo se z1 e z2 sono complessi coniugati.
Dimostrazione:
a) Se z1 e z2 sono complessi coniugati saranno del tipo:
z1 = a + ib; z2 = a – ib a, b appartenente ad R
Allora il prodotto (x-z1) . (x-z2) risulterà:
x2 –(z1+z2)x+(z1 z2) = x2-2ax+(a +b )
cioè un polinomio di secondo grado a coefficienti reali.
b) Viceversa se z1 = a1+ ib1, z2 = a2 – ib2 sono due numeri complessi non reali, consideriamo il prodotto:
(x-z1) . (x-z2) = x2 –(z1+z2)x+(z1 z2)
Supponiamo che tale prodotto abbia coefficienti reali. Allora (z1+z2) = (a1+a2) +i (b1+b2) per essere reale deve avere b1+b2 = 0 cioè b1 = -b2.
Anche (z1 . z2) = (a1b1-a2b2)+ i (a1b2+a2b1) dovendo essere reale deve avere:
a1b1+a2b2 = 0
Sostituendo:
a1b1+a2b2 = a1b1- a2b1 = 0
Esseno z1 non reale e quindi b1diverso da 0, segue:
a1 = a2
Cocludendo z1 e z2 sono complessi coniugati avendo a1 = a2 (parte reale uguale) e b1 = -b2 (parti immaginarie opposte).
Teorema fondamentale dell’algebra: Una equazione polinomiale di grado n e a coefficienti reali ha n soluzioni nell’insieme dei numeri complessi.
Conseguenze del teorema fondamentale:
Ogni polinomio a coefficienti reali di grado n si può sempre scomporre (in modo unico) nel prodotto a (x-z1) . (x-z2) ... (x-zn), essendo a appartenente ad R e z1, z2, ... , zn appartenenti a C.
Se un polinomio a coefficienti reali ha come zero il numero complesso non reale z, allora anche il complesso coniugato di z è uno zero per quel polinomio. In altri termini i numeri complessi non reali soluzioni di una equazione polinomiale sono sempre a coppie e quindi sono in numero pari.
Forma trigonometrica dei numeri complessi
Oltre alla forma algebrica a+ib, è possibile scrivere i numeri complessi in una forma trigonometrica. Osservando infatti la figura 3
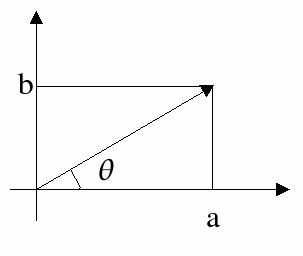
fig. 3
si vede che a = r cos e b = r sen dove naturalmente r è il modulo del numero complesso. Quindi:
a+ib = r (cos +i sen )
Se si esegue l'elevamento al quadrato si ha:
r2 (cos +i sen )2 = r2 (cos2 -sen2 +2 i sen cos )
applicando le formule di duplicazione:
r2 (cos +i sen )2 = r2 (cos 2 +i sen 2)
Questa formula si può generalizzare:
rn (cos +i sen )n = rn (cos n +i sen n)
Quest'ultima è la formula di De Moivre.
Partendo da questa formula è possibile ricavare le formule per il seno e il coseno di 3n, 4n, 5n e così via.
E' possibile dare una forma esponenziale ai numeri complessi:
ei = (cos +i sen )
Questa è detta formula di Eulero. In base ad essa si ha:
ei0 = (cos 0 +i sen 0) = 1
ei = (cos +i sen ) = -1
In quest'ultima espressione si evidenzia una relazione fra numeri molto importanti nella matematica:
ei +1 = 0
Questi appunti sono tratti da:
Maraschini Palma “Conoscenze matematiche 1” ed. Paravia
Lombardo Radice Mancini Proia “Il metodo matematico” vol. 3 ed. Principato
S. Maracchia “Da Cardano a Galois Momenti di storia dell'algebra” ed. Feltrinelli
Dodero et al. “Nuovo corso di trigonometria” ed Ghisetti e Corvi