Le coordinate dei centri ed il raggio dei cerchi gemelli di Archimede

Per individuare le coordinate dei centri ed il raggio dei cerchi gemelli di Archimede (sono quelli di centro K e K') si può intanto osservare che ciascun cerchio è tangente al semicerchio grande, ad uno dei semicerchi piccoli ed al segmento DG. Conviene intanto definire:
r2 raggio AE
r3 raggio DF
r4 raggio AC
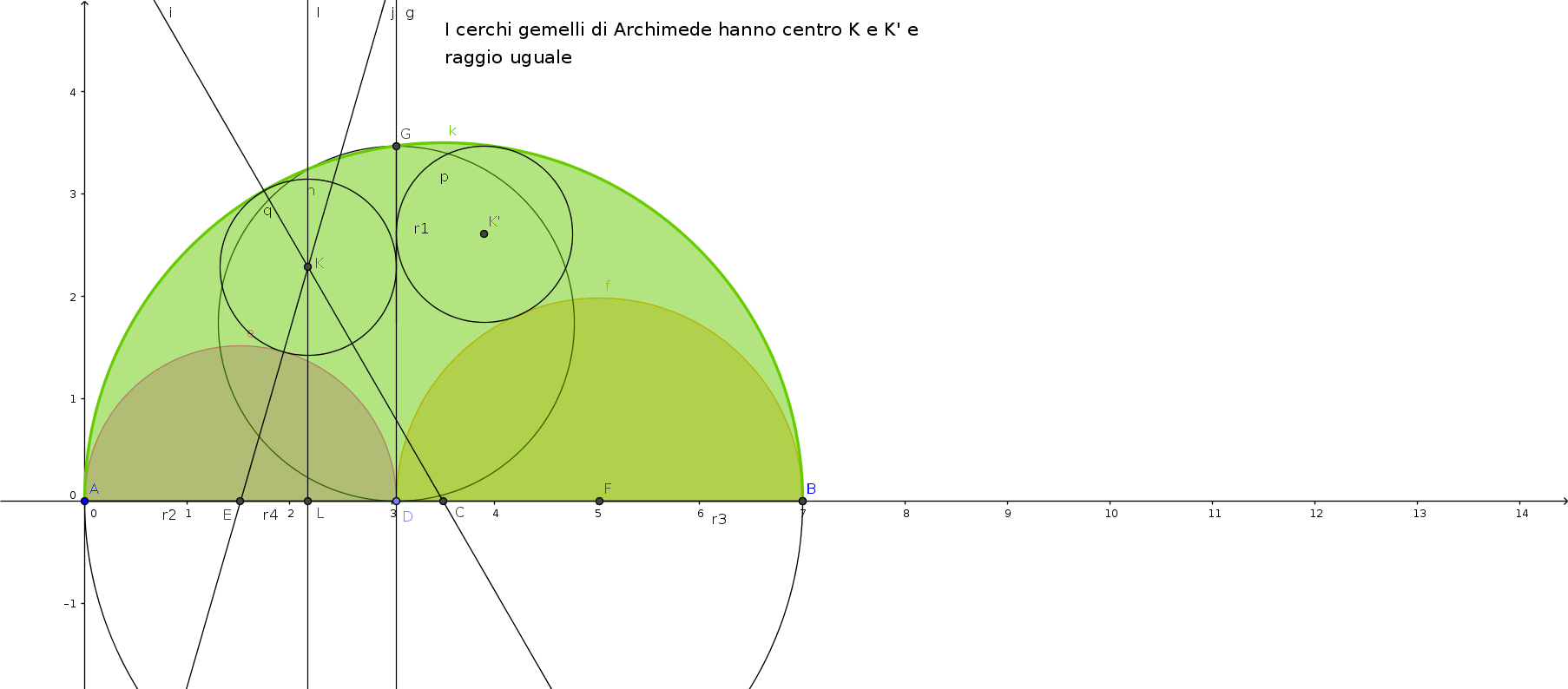
Noti questi tre raggi si tratta di trovare
le coordinate di K (α;β) in un riferimento cartesiano di centro A
R raggio dei cerchi gemelli.

In sostanza si tratta di applicare Pitagora a due triangoli che ora individueremo e di una considerazione sulla ascissa α

Osserviamo il triangolo rettangolo EKL
l'ipotenusa EK è lunga r2+R
il cateto KL è proprio β
il cateto EL è dato da r2-R dal momento LD è uguale a R

Inoltre AL=α, AD=2· r2 segue R=2·r2-α.
Applicando Pitagora al triangolo EKL si ha:
(r2+R)2 =β2 + (r2-R)2
4 · r2 · R = β2
sostituendo il valore di R
4 · r2 · (2·r2-α) = β2 (1)

Cambiando la posizione del punto D nel diametro AB, le espressioni dei lati del triangolo possono diventare l'opposto ma questo non comporta problemi dato che tali espressioni sono state usate con Pitagora al quadrato.
Passiamo ad esaminare il triangolo rettangolo LKC
l'ipotenusa KC è lunga r4-R
il cateto LC è dato da r4-α (dato che AL è α)
il cateto LK è proprio β come prima.
Sempre con Pitagora
(r4-R)2 = β2 +(r4-α)2
(r4-2·r2+α)2= β2 +(r4-α)2
Sostituendo la (1) a β2 ed eseguendo alcuni passaggi si ottiene

α=r2·(r2+r4)/r4


Noto α si trova β con la (1)

β2=4·r22(r4-r2)/r4

Ed anche il valore di R:

R=2·r2-α=r2 (r4-r2)/r4

In base alle indicazioni sui raggi, si può scrivere:

2·r2+2·r3=2·r4
r2+r3=r4

Ciò posto R si può riscrivere:

R=r2·r3/(r2+r3)


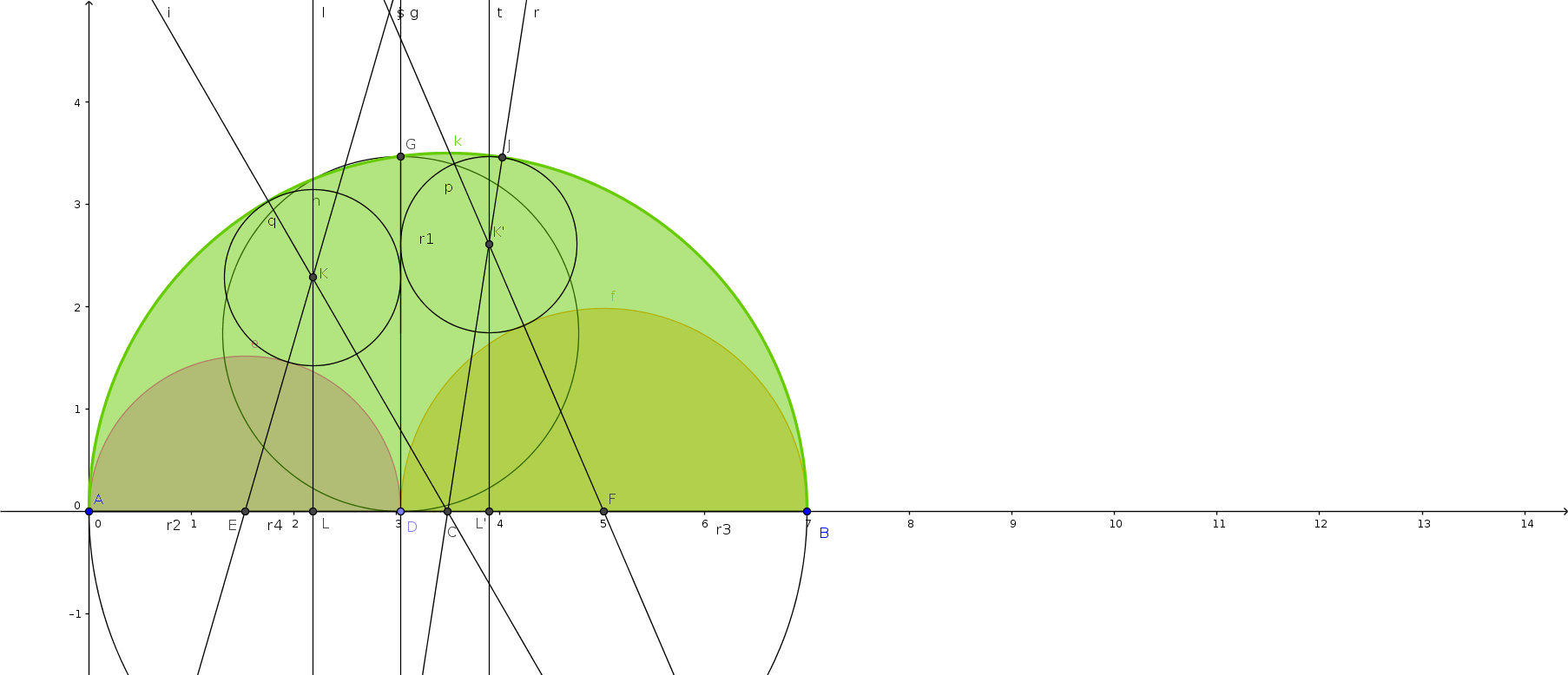
Anche per trovare le coordinate del secondo cerchio gemello si può procedere in modo analogo utilizzando Pitagora.
Indichiamo le coordinate di K' con α e β.
Avremo che α=2·r2+R

Osserviamo il triangolo rettangolo K'L'C
ipotenusa K'C=r4-R=r4+2·r2-α
cateto K'L'=β
cateto L'C=r4-α
Per Pitagora si può scrivere:
(r4+2·r2-α)2=β2+(r4-α)2

semplificando:
β2=4·r2 (r2+r4-α)

Si consideri ora il triangolo rettangolo K'L'F
ipotenusa K'F=r3+R=r3-α+2·r2=r4-r2+α-2·r2=r4+α-3·r2
cateto K'L'=β
cateto L'F=r3-R=r3-α+2·r2=r4-r2-α+2·r2=r4+r2-α

Per Pitagora: (r4+α-3·r4)2=β2+(r4+r2-α)2

Sostituendo β2 e semplificando, si trova:

α=r2·(3·r4-r2)/r4)

E quindi di β:

β2=4·r2 (r4-r2)2/r4

Riassumendo, il centro del cerchio gemello più vicino ad A è:



L'altro centro avrà coordinate: