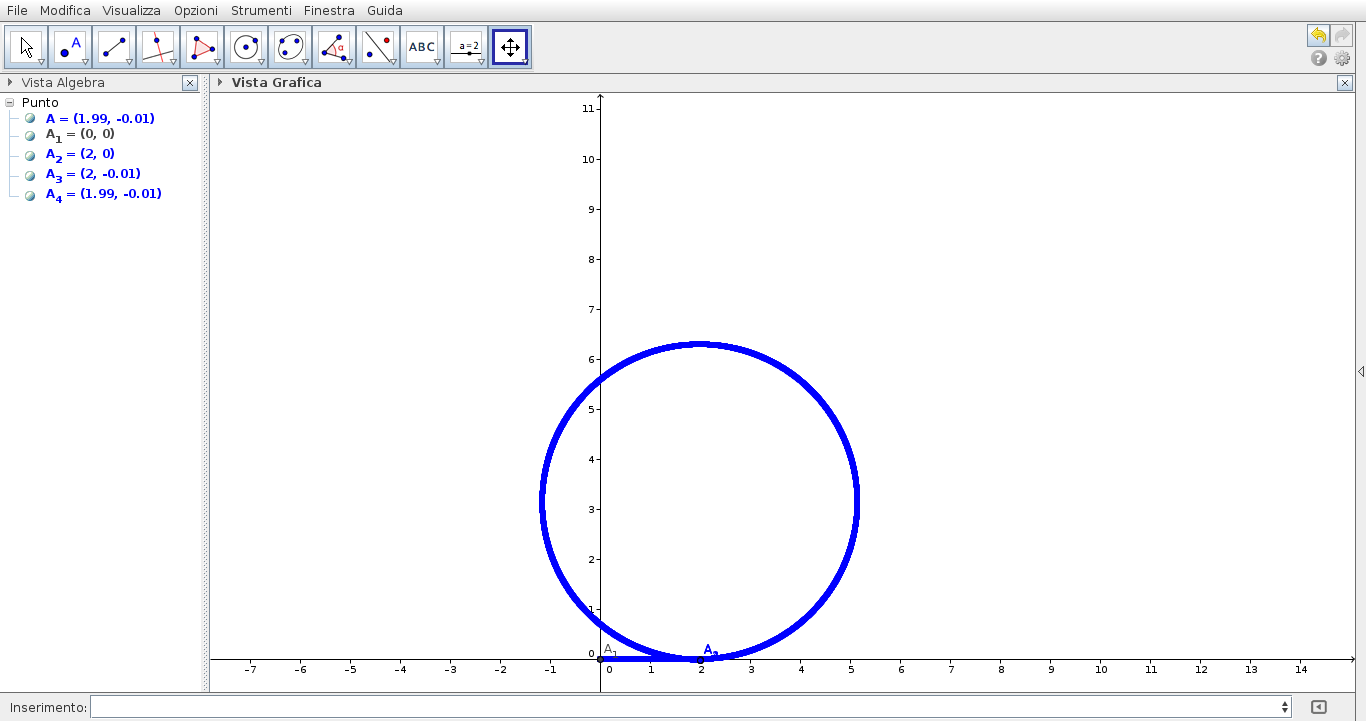
Utilizzando il calcolo ricorrente approssimato è possibile simulare il moto di un elettrone prima dentro un campo elettrico per far aumentare la velocità e dopo dentro un campo magnetico. Questo moto avviene ad esempio dentro l'apparato per calcolare il rapporto carica massa dell'elettrone.
Dopo aver aperto il GeoGebra
5 ed anche il Python
incorporato
si prenda un punto A nell’origine e si copi il seguente codice (dopo # il commento che non influisce sul codice):
e=1.6E-19 # C carica
elementare
m=9.11E-31#kg massa elettrone
dt=0.6E-11 # s
B=1.4E-3 #T campo magnetico
V=1.7E2 # Volts
dist=0.02 # m
Ele=V/dist #V/m campo elettrico
$A=(0,0)
$A.trace=True# traccia attiva
def vai():
k=100 # fattore di scala
t=0
x=0 #m
y=0
vx=0 #m/s 3.000001E4
vy=0
FE=e*Ele # N Forza elettrica
ax=FE/m
while x<=0.02:
vx=vx+ax*dt
x=x+vx*dt
t=t+dt
$A.coords=(x*k,y*k)
#fine campo elettrico, inizio campo magnetico
t=0
r=m*vx/(e*B)
periodo=(2*3.14*r/vx)
# il periodo di una rotazione e' dato da
2*pgreca*r/vx
while t<=periodo:
Fqx=-(e*vy*B) #formule per il
prodotto vettore, la carica e negativa
Fqy=e*vx*B
ax=Fqx/m
ay=Fqy/m
vx=vx+ax*dt
vy=vy+ay*dt
x=x+vx*dt
y=y+vy*dt
t=t+dt
$A.coords=(x*k,y*k)
Il primo ciclo di
ripetizioni while serve per calcolare la velocità raggiunta
dall'elettrone finchè esso si trova nella zona dove agisce il campo
elettrico (di direzione uguale all'asse x e verso opposto) in questo caso da zero fino a 0.02 m.
Dopo inizia la zona dove
agisce il campo magnetico (che si immagina di direzione perpendicolare
al piano xy e diretto dal monitor verso chi guarda) e bisogna calcolare
la forza di Lorentz con
un prodotto vettore. Dati i vettori a di componenti [a1, a2, a3] e b di componenti [b1, b2, b3], le componenti del prodotto vettore si trovano così:
a × b = [a2b3 − a3b2, a3b1 − a1b3, a1b2 − a2b1]
Tenendo conto che la carica dell'elettrone è
negativa dobbiamo considerare che nel calcolare qv vettor B (prodotto
vettore) q è negativa.
La velocità v ha solo le due componenti x e y cioè 1
e 2. Il moto avviene su di un piano mentre il campo B ha una unica
componente z cioè 3.
Ecco allora spiegato perchè:
Fqx=-(e*vy*B)
Fqy=e*vx*B
Dopo aver copiato il codice
rispettando il rientro delle colonne, eseguire Edit e Run Script e dopo
nella riga di comando di Interactive, scrivere vai() e invio.
