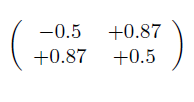
Matrici 2X2 per trasformazioni geometriche
Simmetria assiale
Per introdurre in GeoGebra una matrice, si utilizza una lista di liste che sono le righe della matrice. Ci si serve delle parentesi graffe per racchiudere gli elementi della lista. Ecco un esempio da scrivere nella riga di comando:
A è una matrice 2X2 formata da due righe; la prima è data da -0.5 e 0,87; la seconda riga è data da 0.87 e 0.5. Ovviamente la rappresentazione con GeoGebra sarà simile a questa:
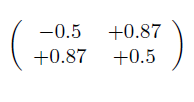
Con GeoGebra è facile applicare la trasformazione geometrica corrispondente alla matrice A ad un punto qualunque: basta definire un punto B e moltiplicare la matrice A per il punto B considerato come un vettore con una componente x e una y ovvero una matrice di due righe ed una colonna.
B'=A*B
Definire in questo modo la trasformazione di un poligono vertice per vertice.
Dato che la matrice trasposta e la matrice inversa di A coincidono, si tratta di una simmetria assiale. Per individuare l'asse della simmetria geometricamente, si può chiedere di trovare l'asse del segmento di un punto e del suo simmetrico.
La pendenza o coefficiente angolare h di questo asse permette di trovare l'angolo fra la retta e l'asse x :
i= atan(h)
L'arcotangente in GeoGebra si indica con atan.
La matrice di una simmetria assiale rispetto una retta passante per l'origine con un angolo α rispetto l'asse x è data da:
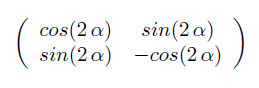
Basta adesso calcolare cos(2 i) e sin(2 i) per verificare che si riottiene la matrice di partenza.
