Campo magnetico con il GeoGebra

Campo magnetico nello spazio a tre dimensioni creato da un filo rettilineo percorso dalla corrente elettrica i, in un punto individuato dal vettore r. sono i versori (vettori di modulo 1 che indicano la direzione) del filo e del vettore r. |r| indica il modulo di r. X indica il prodotto vettore.

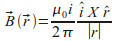
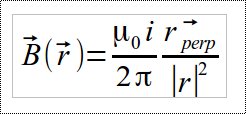
r_perp indica il vettore perpendicolare ad r ottenuto con una rotazione di r di 90⁰ in senso antiorario.

Al denominatore compare il quadrato del modulo di r. Infatti B deve avere direzione e verso di r_perp  e dividendo questo vettore per il suo modulo si trova un vettore di modulo unitario ma avente direzione e verso giusti. Il campo B deve inoltre essere inversamente proporzionale alla distanza ed ecco perchè nella formula si deve dividere per il quadrato del modulo.

Con GeoGebra, si disegni un punto A nell'origine degli assi. Questo punto indica un filo elettrico perpendicolare alla pagina e verso chi legge.

Si prenda un punto  B  qualunque.  Il primo risultato sarà trovare il campo magnetico in B.
Si definisca il vettore r che va da A in B (vettore posizione).

Il vettore perpendicolare si può semplicemente trovare con :

r_perp   = (-y(r), x(r))

In altre parole il vettore perpendicolare si ottiene prendendo come componente x, la componente y di r cambiata di segno;
come componente y si prende la componente x di r (basta eseguire un grafico in un foglio quadrettato per convincersi). Ovviamente in GeoGebra x(r) indica la componente x di r ed analogamente per y.
I due vettori r ed r_perp  hanno lo stesso modulo.

Dopo aver scritto nella riga di comando i valori di i ad es. 50 ed aver definito µ₀ , si può passare a calcolare il vettore di B utilizzando la formula scritta sopra.

Caratteristica dei vettori è quella di essere inizialmente applicati nell'origine. Per ottenere il vettore applicato nel punto B, bisogna in GeoGebra operare un traslazione:

Trasla[nome vettore, punto iniziale]

Nella rappresentazione il vettore risulta di modulo piccolissimo ed allora è necessario moltiplicare il vettore per un fattore di scala ad es. 1.5E6
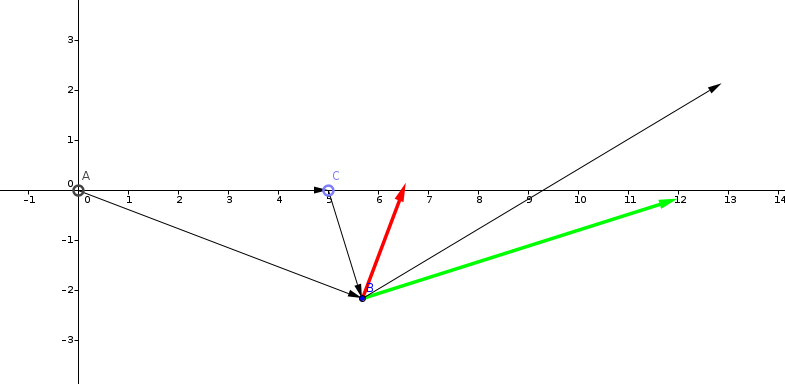
Si ottiene così il vettore disegnato in rosso nel precedente grafico.

Volendo introdurre un altro filo parallelo  al primo  e passante da un punto C  si procede nello stesso identico modo e si ottiene  il vettore  colorato in verde  nel  grafico.

Adesso basta sommare i due vettori per ottenere  il campo magnetico risultante.  Le operazioni con i vettori sono predefinite nel GeoGebra.

Muovendo il punto B si ottiene il campo risultante in quel punto.