Formule inverse utili:

Lunghezza d'onda:

λ=   V

f

Lunghezza d'onda:è la distanza che

λ=T * V

T= 1

la tensione percorre in un periodo.

f

V=Velocità della luce (3*10^8)

T=Periodo

λ=sinusoide di diversa ampiezza.

Nota se aumenta f diminuisce il periodo.

Cavo coassiale:

Linea Bifilare:

L=induttanza

C= Capacità

L=  μ           *

ln *   ( b)

L=induttanza

L=  μ           *

ln *   (2 d)

2π

a

C= Capacità

π

a

C = Ct         =

2π * ε

C  =        π * ε

h

ln *   ( b)

ln *   ( 2d)

a

a

R =     1     *

ρ * f * μ *c         *

1   +   1

R =    2     *

ρ * f * μc

2

π

a         b

b

π

Strip Line:

Costanti utili per le formule dei mezzi trasmissivi:

L=   μ          *

( b)

ε = εo * εr

Nota questo è il valore di ε

a

nel vuoto.

C =              ε    *

( b)

εo=(1/(36 * π)*(10^ -9))

εo=Costante dielettrica del

a

dielettrico.

R =    2         *

ρ * f * μc

μ  = 4π *(10^ -7)

Permiabilità magnetica del

b

dielettrico nel caso del vuoto

Note:

Impedenza Caratteristica:

Zo =V+(x)

Le formule qui utilizzate rappresentano

V-(x)

il caso ideale di linea.Cioè una linea

priva di perdite.

Zo =

Z

Y

R+JωL

L

G+JωC

C

Note:

Γ=

Z * Y

Le formule qui utilizzate rappresentano

il caso ideale di linea.Cioè una linea

priva di perdite.In questo caso alfa

(R+JωL)*( G+JωC)

è uguale a 0 e qundi:

Γ=α+Jβ

La costante alfa si chiama costante di

quindi:  Γ=α+Jβ

propagazione, se è puramente

immaginaria la linea è priva di perdite

quindi:R=0;G=0.Se alfa è immaginaria

la linea è con perdite R=0,G=0.

Velocità di propagazione:

Note:

Vp= α

α=Pulsazione in radianti

β

β=costante di fase

Vp=     1

L*C

il caso ideale di linea privo di perdite.

Coefficiente di riflessione,di corrente e di tensione:

Γi=   I -

Γv=   V -

I+

V+

DOVE:

ΓV=   ZL-Zo

ZL:IMPEDENZA DI CARICO

ZL+ZO

ZO:IMPEDENZA CARATTERISTICA

Nel caso in cui ZL=ZO:

ΓV =0

Rapporto V / I in un qualsiasi punto della linea:

Note:

Z(d) =

V(d)

Dove: β = 2π

I(d)

λ

Zo* (ZL+JZo*Tgβd)

Consideriamo d il punto a partire dal carico

Zo+JZL*Tgβd

Z(d) = (1+ Γv (d))

(1 - Γv (d))

Onda diretta e onda riflessa:

Ros:Varia tra uno e infinito.

Γv=   V -(d)

Formula inversa utile:

V+(d)

( 1-Γ )*R=1+Γ

R-Γ R=1+Γ

ROS=  1+  Γv

R-1=Γ+Γ R

R-1=Γ(R+1)

1-  Γv

Γ=

ROS-1

ROS+1

Onda onda riflessa totale:

es

Zo

1° CASO(cortocircuito):

Sul carico:un nodo di corrente un

ZL=0

ventre di tensione.

ΓV=   ZL-Zo

Zo     =  -1

Z(d)=J*Tgβd

Varia con la funzione tangente

ZL+ZO

2° CASO(circuito aperto):

es

ZL=∞

Z(d)=

Zo* (ZL+JZo*Tgβd)

-1

Γ V         1

Zo+JZL*Tgβd

Z(d)=    Zo

JZo

J*Tgβd

Tgβd

Metodi di adattamento in impedenza:

Note:

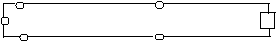
In questo primo caso non

es

Zo

ZL

ZL SIA REALE=RL

abbiamo più onda riflessa

e quindi non c'è più

dispersione.Quindi tutto il

1° CASO(ZL=Z0):

segnale va tutto sul carico.

Adattamento:

es

Zo

RL

Zo' =     Zo*RL

media geometrica

2° CASO(ZL non sia reale):

Note:

Si deve inserire il tratto di linea

lungo  λ/4,ad una distanza L del

carico,dove l'impedenza risulta

puramente resistiva.

Questo equivale a trovare

es

Z'o

Zo

ZL

un trovare un nodo a un

o un antinodo di tensione dove

λ/4

L

l'impedenza assume

rispettivamente il valore Rmin

Zo' =     ZR min

quando scelgo Rmin

o Rmax.

Zo' =     ZR max

quando scelgo Rmax

n1= C            ;

n2= C                             Dove c è la velocità della luce 3 * 10^8

μ1

μ2

Legge di Snell:

Note:

sen α     =    n2

NA =No sen αm dove No è l'indice di riflessione

sen β           n1

del mezzo trasmissivo in cui avviene

l'accoppiamento sorgente-fibra.

αm = arcsen NA

sen α =   n2

αL =  arcsen  n2

n1

n1

No = 1             se si considera l'aria

NA = sen αm

Numero di modi:

Formula di eurelo:

2

e(α+ - Jβ) * x = e αx * (cos βx + - Jsen βx)

P =0,5 *  π * d *NA

λ

Per rendere la fibra monomodale:

Formule inverse utili:

2

NA=       (n1)^2 - (n2)^2

β= 2π * f

β= 2π

P =    0,5  π * d *NA

2

V

λ

λ

n2=       (n1)^2 - (NA)^2

V =     c

εr

d =            2    *  λ

n1=       (n2)^2 + (NA)^2

0,5 *    NA *  π

Lambda cut-off:

Definizione:

λ=         2        π   * D * NA

Lambda cut-off è la lunghezza d'onda minima della luce che

2

può propargarsi all'interno della fibra ottica.

Dispersione modale:

Definizione:

Δt = l * n1 *(n1 - n2)

La differenza di tempo di propagazione tra i due raggi limite

c   n2

Δt viene detta dispersione modale.

Banda passante modale:

Banda passante effettiva:

Nota:

f MAX =  1

B =        1

Per aumentare la banda

2Δtm

1   +   1

passante si può ridurre quasi

b^2m   b^2c

a zero la dispersione cromatica

Bm = f MAX - 0

,in modo da rendere trascurabile

2Δtm

il termine Bc,utilizzando come

Banda passante cromatica:

sorgente un diodo laser che

emette luce a elevata purezza

Bc = 1    =   1

cromatica:

2 Tg      2m Δλ

(monocromatica Δλ =1-3 nm).

Potenza persa:

Potenza ingresso:

Potenza che arriva sul carico:

2

no = 1 (aria)

Pp =     n1-n0

Pi = K * π * (1/2 * dc * NA )2

Pi - Pp

n1+ n0

dove: k=0,85

dc= diametro core