Light-induced drift of rubidium upon optically thin regime
A. Lucchesini, S. Gozzini and L. Moi
Light-induced drift (LID) has been deeply studied during these last
years with special attention to the alkali-noble gas systems [1]. The LID
effect consists in a macroscopic diffusion of an active gas immersed in a
buffer gas. This diffusion, that may reach velocities of the order of 10-50
m/s, appears when both a velocity selective excitation and a transport property
dependence on the atomic internal states are present. The diffusion is along
the laser beam propagation and its direction depends on the laser frequency
detuning. The LID pressure, which is due to atomic momentum transfer and not to
photon momentum exchange, can be orders of magnitude larger than the radiation
pressure and, for this reason, it is suitable for many applications. Isotope
separation seems to be the more promising and convenient when diode lasers can
be used, and among the alkali atoms, rubidium is the best candidate. It has two
stable isotopes 85Rb and 87Rb, with relative concentrations equal to 72% and 28% respectively. The
absorption spectrum, as shown in fig. 1 in the case of D2 excitation, has four well separated
lines, each one being due to the absorption of one isotope at a time. Streater et al. [2] calculated the drift velocity as a function
of the laser detuning and they found that at some frequencies the two isotopes
can also diffuse to opposite directions. Therefore the approach seems straightforward:
the laser can be slightly detuned with respect to the absorption line of one of
the two isotopes, which is then pushed away and collected. In the practice
many problems come out and an effective isotope separation seems more
troublesome.
The analysis of the cell wall contribution to the vapor dynamics is
stressed out by taking into account the new light-induced atom desorption
effect (LIAD), recently observed.
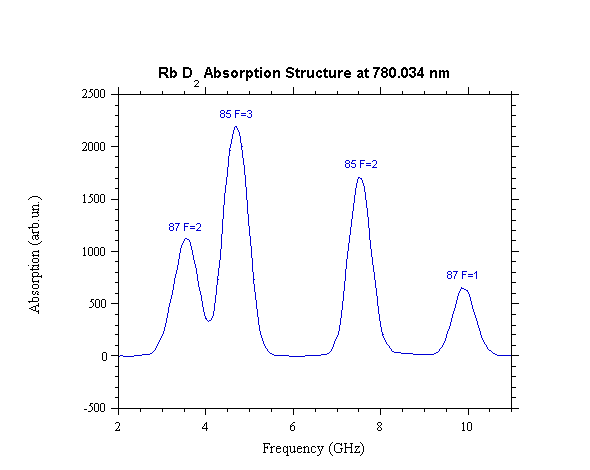
Fig. 1. D2 absorption spectrum of both
rubidium isotopes.
LID VELOCITY CALCULATION
The drift velocity can be calculated by considering the atom level
structure and the impact parameters with the buffer gas. In principle the
complete level structure should be taken into account, but, as shown by
Haverkort et al. [3], a simplified atom model can be conveniently adopted. This
numerical model has been first developed and checked for a four-level alkali
atom model based on realistic Keilson-Storer collision kernels. This gives a
good agreement between theory and experimental results in the case of sodium,
as discussed by Werij et al. [4]. The four levels are the two hyperfine ground
states and the two excited fine-structure states. For heavier alkali atoms like
Rb, the collision transfer rate between the two fine-structure levels can be
neglected and in this specific case, when only one of the two upper levels is
optically excited [5], a simpler three-level description is possible. Rb atom
is then described by the two ground hyperfine states (labelled 1 and 2) and by
one excited state (labelled 3). The rate equations can be written in the form:
![]() (1)
(1)
where
 (2)
(2)
is the population distribution, A and B are 3x3 matrices,
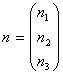 (3)
(3)
with
![]() (4)
(4)
and
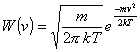 (5)
(5)
By remembering that the drift velocity is given by
![]() (6)
(6)
it results
![]()
 (7)
(7)
where
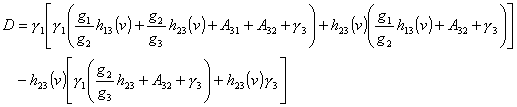 (8)
(8)
and
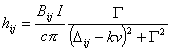 (9)
(9)
hij are the excitation rates at a given velocity, Bij and Aij the Einstein coefficients, gi the statistical weights of the
levels, I the laser power density, gi the collision rates.
Table I.
Common parameter values.
|
Parameter |
Ref. |
Value |
|
g1,2 |
3, 6 |
3.18×107 Hz |
|
g3 |
3, 6 |
4.15×107 Hz |
|
A3 |
5 |
3.66×107 Hz |
|
Is |
7 |
361.88 W×m-2 |
|
k |
|
0.8055×107m-1 |
|
G |
7 |
2.93×108 Hz |
|
T |
|
333 K |
Table II. Specific parameter values. DHFS is the hyperfine energy level
distance.
|
Parameter |
Ref. |
85Rb value |
87Rb value |
|
A31 |
5 |
2.135×107 Hz |
2.288×107 Hz |
|
A32 |
5 |
1.525×107 Hz |
1.372×107 Hz |
|
g1/g3 |
5 |
7/24 |
5/16 |
|
g2/g3 |
5 |
5/24 |
3/16 |
|
DHFS |
5 |
3.0 GHz |
6.8 GHz |
The equation (7) has been numerically integrated by adopting the
parameter values reported in tables I and II, and by assuming
that the cell is filled with 5 Torr of Kr as a buffer gas. In fig. 2 the
drift velocity v calculated as a function of the laser detuning is shown
for the two isotopes. The laser power density is assumed equal to WL= 10 W/cm2 and the laser is single mode.
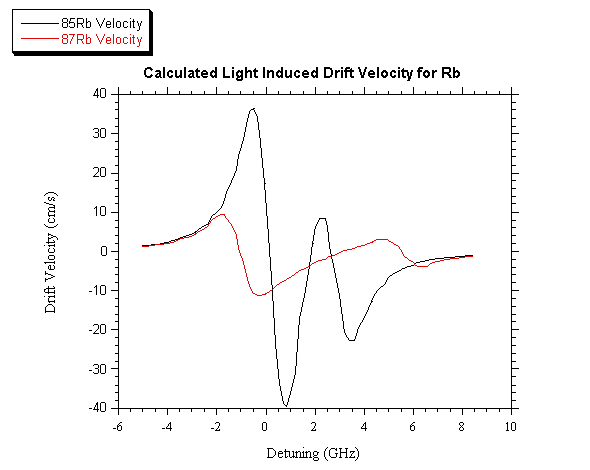
Fig. 2. Drift velocity of the two Rb isotopes calculated as a function of
the laser detuning, when the laser power density is 10 W/cm2
In fig. 3 v is shown as function of the laser power
density WL, at the frequency detuning DnL = -0.5 GHz. With this frequency
detuning the two isotopes drift to opposite directions, with a relative velocity
of about 40 cm/s when the laser power density is equal to 10 W/cm2.
These calculations clearly show that, upon our experimental conditions, both
rubidium LID and isotope depending velocities can be obtained. The only
limitation set with this approach is the “optically thin condition” imposed to
the vapor.
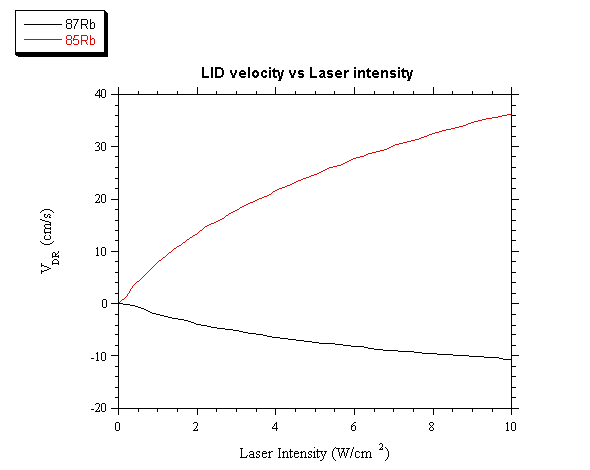
Fig. 3. Drift
velocity of both isotopes as function of the laser power density at a fixed
laser detuning equal to -0.5 GHz.
LID VELOCITY MEASUREMENTS
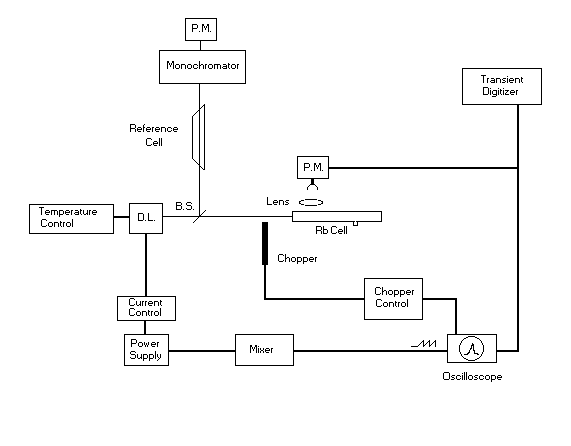
Fig. 4.
Sketch of the experimental apparatus for the LID effect. D.L.: diode
laser, P.M.: photomultiplier, B.S. beam splitter.
The experimental apparatus is sketched in fig. 4. AlGaAs single
mode diode lasers, operating in free running mode, are used for excitation and
monitoring of Rb vapor. Their gross frequency tuning is achieved by driving
the diode laser temperature by using the Melles Griot thermoelectric cooler 06
DTC 001. The Melles Griot current generator 06 DLD 201 controls the fine tuning
by the laser injection current. The LID laser, tuned to the D2 line of rubidium, is sent to a
capillary cell (2 mm internal diameter, 15 cm long and filled with 5 Torr of
Kr). The cell is coated by an ether solution of dimethylpolysiloxane that
reduces the vapor friction at the cell walls as described in ref. [8].
The LID effect is recorded by detecting the fluorescence coming from a
given point along the capillary. The laser pushes or pulls the atoms and the
detected fluorescence variations can be related to the vapor diffusion. Two
different approaches have been adopted, with the aim of well displaying the
LID effect. In the first one the laser frequency is kept fixed and the laser is
switched on at a given time. The fluorescence decay allows us to derive the
drift velocity. In the second one the laser is always on, but its frequency is
swept across the resonance. Depending on the different contribution of optical
pumping and LID, the spectrum results modified by changing the scanning
velocity. It is possible to separate these two contributions and extract the
LID effect only; in such a way a continuous dependence of the drift velocity on
the laser frequency is obtained. In these measurements only the total diffusion
of the vapor, related to both isotopes, has been studied.
The macroscopic diffusion of the vapor is described by the differential
equation
![]() (10)
(10)
where D is the diffusion coefficient of the ground state atoms. The
solution of this equation for an optically thin vapor and for the boundary
conditions
![]() and
and ![]() (11)
(11)
has been already given and checked for sodium [2]. The solution having
the form:
![]() (12)
(12)
where
![]() (12a)
(12a)
and
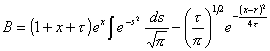 (12b)
(12b)
with x= (v/D)×z.
The A term value varies between 0 and 1 and assumes the value of 0.5 after
a time t*= z0/v, where z0 is the observation point and v
the drift velocity. The B term contributes by a vanishing quantity,
depending on the parameter S = z0v/D. When S = 1, B is about
0.08 and when S becomes larger, B goes rapidly to zero. Therefore, when
the B term is negligible, v can be directly derived by measuring z0 and t*. In our experimental
conditions S = 0.2 v, and a drift velocity of a few cm/s is
enough to give a B term of only a few per cent, therefore the drift velocity
can be obtained with a reasonably good accuracy. In fig. 5 the fluorescence
variations as a function of time are reported for two different laser
detunings. The signals correspond to the drift of both isotopes. The bottom
line comes from the stray light and permits an absolute evaluation of the vapor
density variation.
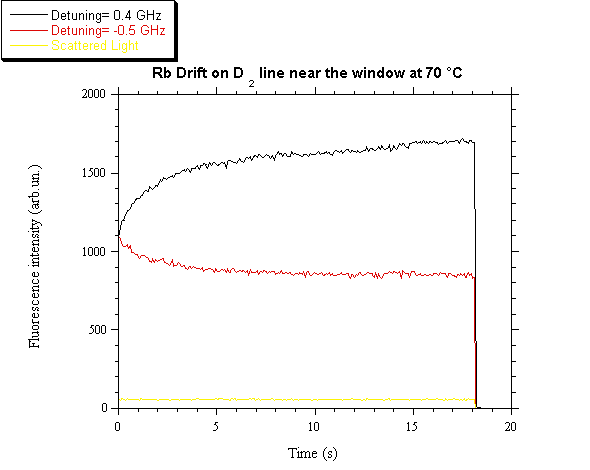
Fig. 5. Fluorescence signals as function of time for
two laser detunings.
The results shown in fig. 6 are obtained by continuously varying
the laser frequency and by looking at the fluorescence spectrum as a function
of the laser frequency scan rate nR. Due to both optical pumping and LID, the
fluorescence spectrum depends on nR, and in place of the four well separated peaks
as reported in fig. 1, only three peaks appear, whose relative intensities
again depend on nR. When nR is decreased to about nR = 1 Hz, the optical pumping
dominates and the three peaks have the intensities shown in fig. 6a.
When nR is further decreased, the induced
vapor diffusion becomes important and LID overcomes the optical pumping. Then
the relative peak intensities change as shown in fig. 6b. Ought to the
much higher laser power and to the much larger drift velocity, that case showed
a so strong LID effect that no evidence of optical pumping was obtained.
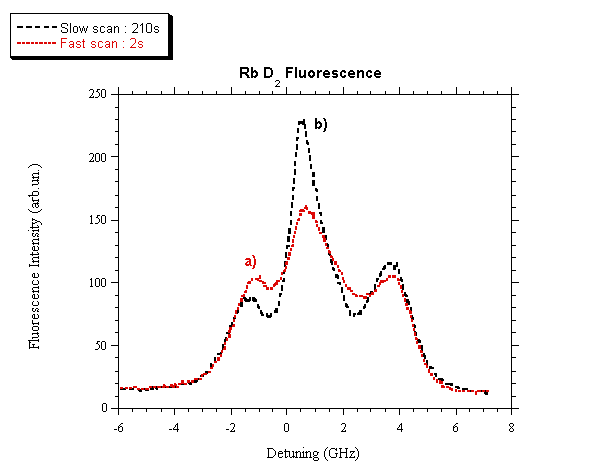
Fig. 6.
Fluorescence spectrum of Rb D2 as a function of the laser
frequency scan rate. a) nR = 0.5 Hz; b) nR = 0.0048 Hz.
By subtracting curve b) from curve a) the LID contribution is obtained
as a function of the laser frequency and the result is reported in fig. 7,
where also the calculated drift velocity and the absorption spectrum without
optical pumping are shown for comparison.
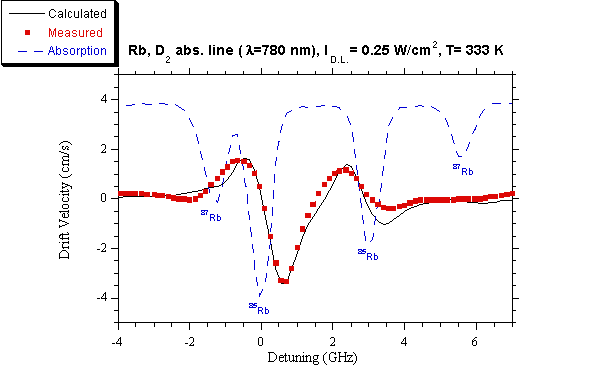
Fig.
7. Drift velocity of Rb, measured and
calculated at different laser detunings from the D2 line. Ilaser = 0.25 W/cm2.
(■) measured velocity, (—) calculated
velocity, (---) absorption feature.
REFERENCES
1. See for example the Proceedings
of The International Workshop on Light Induced Kinetic Effects on
Atoms, Ions and Molecules, Marciana Marina, Elba Island, 2 - 5 May, 1990,
(Ed. L. Moi, S. Gozzini, C. Gabbanini, E. Arimondo, F. Strumia, E.T.S.,
Pisa, Italy, 1991), ISBN 88-7741-560-6
2. A.D. Streater, J. Mooibroek, J.P. Woerdman, Optics Commun. 64,
137 (1987)
3. W.A. Hamel, J.E.M. Haverkort, H.G.C. Werij,
J.P. Woerdman, J. Phys. B: At. Mol. Phys. 19, 4127 (1988)
4. H.G.C. Werij, J.P. Woerdman, Phys. Rep. 169,145 (1988)
5. A.D. Streater, J.P. Woerdman, J. Phys. B:
At. Mol. Opt. Phys. 22, 677
(1989)
6. J.E.M. Haverkort, Ph.D. Thesis, Leiden (1987)
7. E.L. Lewis, Phys. Rep. 58, 1 (1980)
8. J.H. Xu, M. Allegrini, S. Gozzini, E. Mariotti, L. Moi, Optics
Commun. 63, 43 (1987).