RETTE PARALLELE TAGLIATE DA UNA TRASVERSALE
Se
due rette a e b sono tagliate da una trasversale t, si formano otto angoli, come
in figura:
|
|
Si
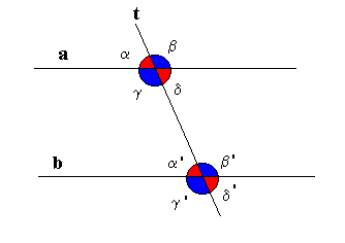
ha, ovviamente, a = d, perché sono opposti al vertice, e, per lo stesso motivo, b
= g,
a'
= d',
b'
= g'.
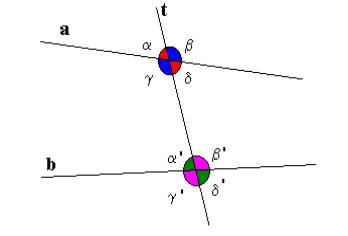
Però, se le rette a e b non sono parallele, non c'è nessuna relazione
particolare tra i quattro angoli formati dalla retta a e i quattro angoli
formati dalla retta b. |
Invece,
se le rette a e b sono parallele, si ha:
|
d = a' e g = b' (angoli alterni interni); a = d' e b = g' (angoli alterni esterni); a = a', b = b', g = g' e d = d' (angoli corrispondenti); g e a' supplementari, d e b' supplementari (angoli coniugati interni); a e g' supplementari, b e d' supplementari (angoli coniugati esterni); |
|
Vale
cioè il seguente teorema:
Se
due rette parallele sono tagliate da una trasversale, allora si formano
angoli alterni interni o esterni uguali, angoli corrispondenti uguali, angoli
coniugati interni o esterni supplementari.
