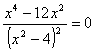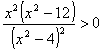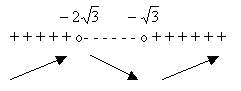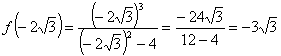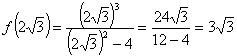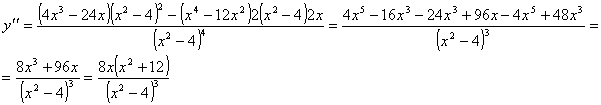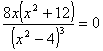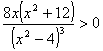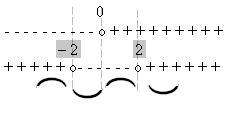|
Studiare la funzione
DOMINIO: INTERSEZIONI CON GLI ASSI
SEGNO DI f(x) y
> 0
S.N.
S.D.
LIMITI E ASINTOTI
Studiamo i limiti negli estremi del dominio
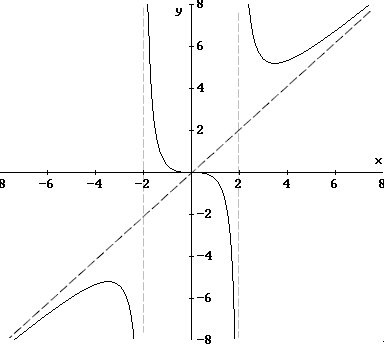
la retta y = x è un asintoto obliquo per f(x)
STUDIO DI f '(x)
STUDIO DI f ''(x)
f(x) ha un punto di flesso nell'origine O(0,0) Concludiamo lo studio con una bozza del grafico di f(x):
|
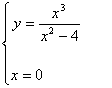
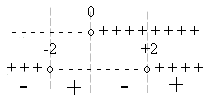
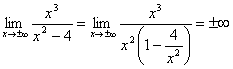 la curva potrebbe possedere asintoti obliqui y = mx + n
la curva potrebbe possedere asintoti obliqui y = mx + n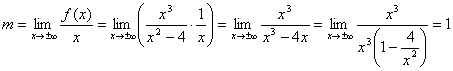
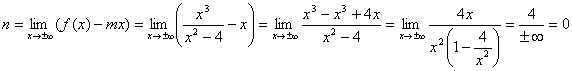
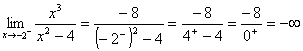 la retta x=-2 è un asintoto verticale per f(x)
la retta x=-2 è un asintoto verticale per f(x)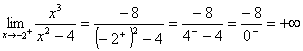 completo
completo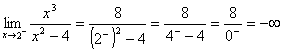 la retta x=2 è un asintoto verticale per f(x)
la retta x=2 è un asintoto verticale per f(x)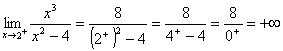 completo
completo