Torna indietro

Risoluzione STUDIO DI FUNZIONE

Studiare la funzione  

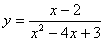
DOMINIO:
f(x) è una funzione razionale fratta; essa è definita per , cioè per
quindi il dominio è
 

INTERSEZIONI CON GLI ASSI

           f(x) passa per il punto A(0,-2/3)

            f(x) non incontra l'asse x

SEGNO DI f(x)

y > 0                      Studiamo il segno del numeratore e del denominatore e quindi della frazione:

SN                    per      x>2  SD         per x<1, x>3

LIMITI E ASINTOTI

Studiamo i limiti negli estremi del dominio per controllare se f(x) possiede asintoti.

                la retta  y=0 è un asintoto orizzontale per f(x)

             la retta x=1 è un asintoto verticale per f(x)

            completo

      la retta x=3 è un asintoto verticale per f(x)

        completo

STUDIO DI f '(x)

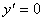
                     nessuna soluzione reale  

f(x) non possiede punti di massimo e di minimo

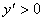
            Poiché il denominatore è positivo (perché elevato al quadrato) e il numeratore è negativo ( possiede il discriminante negativo e il segno di "a" è discorde con quello del polinomio), la frazione è negativa in tutto il dominio. Si deduce che f(x) è monotona decrescente in tutto il campo di esistenza.                                                                               

STUDIO DI f ''(x)

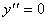
               x - 2 = 0       x = 2         e             

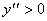
          Poiché la seconda parentesi a  numeratore è positivo per avere il discriminante negativo, il segno della frazione dipende solo dalla prima parentesi e dal denominatore:

             f(x) possiede un punto di flesso in A(2,0)

Concludiamo lo studio con una bozza del grafico di f(x):

 
Torna indietro