Torna indietro

PREPARATI PER L'ESAME ORALE DI MATEMATICA APPLICATA

Questionario con relative risposte

 

Risposte al questionario

  1. Data la parabola di equazione y=-0,05x2+190x-100.000, determinare il punto di massimo, supponendola prima libera da vincoli e poi che sia vincolata da 0 < x < 1.800. Scrivere le coordinate del fuoco, l'equazione della direttrice e dell'asse di simmetria. Fare il grafico.
Risp. 43 -  Trattandosi di una parabola con concavità verso il basso, nel primo caso, quando f(x) è libera da vincoli, il massimo è raggiunto nel vertice V(-b/2a,-∆/4a). In tal caso si ha:

     ;      

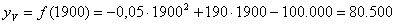
oppure, utilizzando la derivata prima: 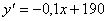   e studiandone il segno, possiamo ritrovare il risultato precedente:

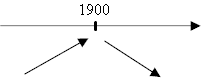
y' = 0       -0,1 x + 190 = 0             x = 190 / 0,1 = 1900

y' > 0       -0,1 x + 190 > 0             x < 1900         f(x) è crescente


 
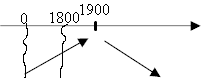
Nel caso in cui la funzione è vincolata per  0 < x < 1.800, risulta che xV=1900 ]0,1800[, ma, essendo f(x) crescente per 0 < x < 1.800, il massimo assoluto è raggiunto nell'estremo destro del campo di scelta e vale:

yG(1800) = -0,5 • 18002 + 190 • 1800 - 100.000 = 80.000

 

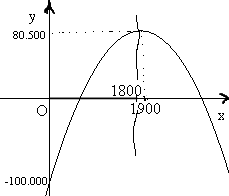
Calcoliamo ora  le coordinate del fuoco, l'equazione della direttrice, dell'asse di simmetria e abbozziamo il grafico.

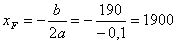
F(1900, 80.495)               coordinate del fuoco

y = 80.505                       equazione retta direttrice

x = -b/2a  x = 1900          equazione asse di simmetria