Torna indietro

PREPARATI PER L'ESAME ORALE DI MATEMATICA APPLICATA

Questionario con relative risposte

 

Risposte al questionario

  1. Descrivi e commenta le operazioni necessarie per studiare una funzione.                             

Risp. 30 - Per giungere al grafico di una funzione occorre studiare:
  1. Il DOMINIO, per stabilire gli intervalli di valori reali per i quali esiste il grafico 

TIPO DI FUNZIONE

CONDIZIONI

OSSERVAZIONI

Razionale intera:

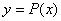
Nessuna limitazione

Tutte le operazioni in P(x) sono consentite

Razionale fratta :

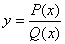
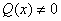
L’unica operazione non consentita è la divisione per 0. Occorre scartare dal dominio i valori di x che annullano il denominatore.

Irrazionale :

 

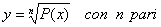
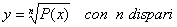
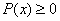
nessuna limitazione

Solo quando l’indice di radice n è pari ci possono essere problemi di estrazione di radice e in tal caso il radicando P(x) deve essere positivo o nullo.

Logaritmica :

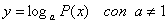
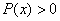
Il logaritmo deve avere l’argomento >0

 
  1. Le SIMMETRIE rispetto all'asse y o all'origine
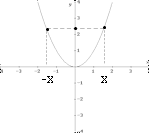
Una funzione y=f(x) risulta simmetrica rispetto all'asse y (funzione pari) se accade che  

f(-x) = f(x)

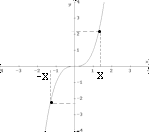
Una funzione y=f(x) risulta simmetrica rispetto all'asse y (funzione dispari) se accade che  

-f(-x) = f(x)

 

 
Lo studio delle simmetrie permette di ridurre lo studio nel primo quadrante e di completare il grafico nel secondo o nel terzo sfruttando la simmetria stessa.

 

  1. La PERIODICITA' di f(x)

          Tale studio si esegue soprattutto in caso di funzioni goniometriche (contenenti seni, coseni, tangenti, ...). 
          Sapere che f(x) è periodica di periodo T, permette di ridurre lo studio nell'intervallo [ 0 , T ]. Il grafico 
          finale si ottiene ripetendo il grafico ottenuto in [ 0 , T ] più volte, prima e dopo l'intervallo stesso.

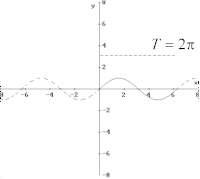
Ricordiamo che affinché f(x) risulti periodica di periodo T occorre verificare che:     f(x+T) = f(x)

cioè, ogni periodo T il grafico si ripete uguale.

          

  1. Le INTERSEZIONI CON GLI ASSI cartesiani
    Basta mettere a sistema la funzione y=f(x) con le equazioni x=0 e y=0 degli assi per conoscere i punti in cui la curva tocca gli assi cartesiani.

 

  1. SEGNO di f(x)

          Basta risolvere le disequazioni f(x) > 0, f(x) < 0 per conoscere gli intervalli di valori reali in cui la funzione è 
          situata sopra l'asse x e quelli in cui è situata sotto l'asse x.

 

  1. LIMITI e ASINTOTI

          Se     allora y = y0 è un asintoto orizzontale per f(x)
          Se 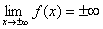  allora f(x) potrebbe avere asintoti obliqui. Bisogna controllare se esistono finiti i limiti:    
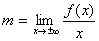            ed   .
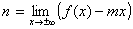          Se 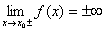 allora x = x0 è un asintoto verticale per f(x)

 

  1. La DERIVATA PRIMA

           Si risolve l'equazione f '(x) = 0 per determinare i punti estremanti ( o stazionari )
           Si risolve la disequazione f '(x) > 0 per scoprire dove f(x) è crescente 
           Si risolve la disequazione f '(x) < 0 per scoprire dove f(x) è decrescente 

           Dal grafico della crescenza e decrescenza si scoprono i punti di massimo e di minimo relativi.

 

  1. La DERIVATA SECONDA

          Si risolve l'equazione f ''(x) = 0 per determinare gli eventuali punti di flesso
          Si risolve la disequazione f ''(x) > 0 per scoprire dove f(x) rivolge la concavità verso l'alto 
          Si risolve la disequazione f ''(x) < 0 per scoprire dove f(x) rivolge la concavità verso il basso 

           Dal grafico della concavità e convessità si scoprono i punti di flesso.