Risp.
8 - Si
definisce dominio o campo
di esistenza
di una funzione y = f(x) l’insieme D degli intervalli formati da
tutti i numeri reali x per i quali è possibile trovare un unico
corrispondente y secondo la legge f assegnata.
In
altre parole il dominio é l’insieme degli intervalli dell’asse
x dove esiste il grafico della funzione nel piano cartesiano.
Si
definisce, invece, codominio
o insieme delle immagini di una funzione f : D → R
l’insieme f(D) 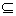 R
dei numeri reali y che sono i corrispondenti dei valori x del
dominio D. Infatti la parola codominio è costituita dalla
contrazione di due parole, da "CO" che sta per
corrispondenti e da "DOMlNIO" (codominio = corrispondenti
del dominio).
Esempi:
Dei
seguenti grafici riportiamo i corrispondenti domini e codomini:
|
|
|
|
|
|
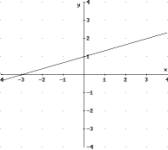
D
= R = ]-¥ , +¥[
f(D) = C = R =
]-¥
, +¥[
-¥
< x < +¥
-¥
< y < +¥
|
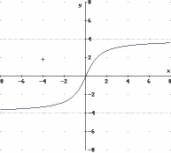
D = R = ]-¥
, +¥[
f(D)
= C = ]-4 , +4[
-¥
< x < +¥
-4
< y < 4
|
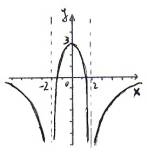
D=]-¥,-2[È]-2,2[È]2,+¥[
f(D) = C = ]-¥
, 3]
x < -2
, -2 < x < 2
, x > 1
y
£ 3
|
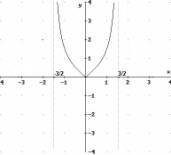
D=]-3/2 , 3/2[
f(D)
= C = [0 , +¥[
-3/2
<
x < +3/2
y ³
0
|
|
