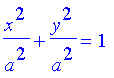
Ecco una costruzione semplice dei punti di un'

Ecco una costruzione semplice dei punti di un' ellisse, con riga e compasso.

CERCHIO

ELLISSE

Fissando x nelle due equazioni e ricavando y² si ottiene facilmente

                          Quindi        HK : HZ =AO : BO

Allora per trovare un punto K dell' ellisse basta tracciare la retta nera verticale, poi la retta AH e infine la retta PB.

   Note

    1) La relazione scritta conduce facilmente al calcolo dell' area dell'
    ellisse.Si immagini di ricoprire le due figure, cerchio ed ellisse, con 
    delle corde verticali( gli indivisibili di Cavalieri). Il rapporto fra le 
     aree è uguale al rapporto fra le corde del cerchio e dell' ellisse, cioè 
    ad a/b. Dall' area del cerchio quindi si ricava subito quella dell' ellisse.

    2)Trovare la relazione in questione per via analitica è banale: 
    per via sintetica lo è assai meno.

    3)L' area dell' ellisse può essere ottenuta immediatamente, pensando 
    l' ellisse come 'dilatata' di un cerchio di raggio 1 mediante la dilatazione

   Si tratta di una trasformazione che dilata le aree di un fattore ab: basta 
   verificarlo per le figure elementari,in pratica per un rettangolo con i lati 
   paralleli agli assi, dato che ogni figura,cui sia attribuibile un' area può
   essere approssimatvamente ricoperta con rettangoli di questo  tipo 
  (entrare nei dellagli di questo problema condurrebbe alla teoria della misura 
   o, che è lo stesso, dell' integrazione e non è questa la sede per farlo).