Analisi e costruzione della risposta in frequenza
I. Diagrammi di Bode [ Margine di Guadagno e di Fase | Banda passante ]
II. Il diagramma di Nyquist [ Il criterio di Cauchy | Stabilità a ciclo chiuso | Margine di Guadagno | Margine di Fase ]
Il diagramma di Nyquist ci permette di studiare la stabilità e le caratteristiche di un sistema a ciclo chiuso osservando il suo comportamento a ciclo aperto. Il criterio di Nyquist può essere usato per progettare, nonostante la stabilità a ciclo aperto (ricorda che il metodo dei diagrammi di Bode presume che il sistema sia stabile a ciclo aperto). Perciò , si usa questo criterio per determinare la stabilità a ciclo chiuso quando il diagramma di Bode mostra informazioni confuse.
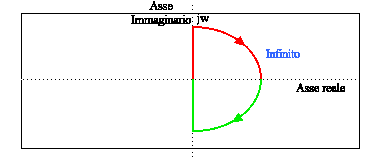
Il diagramma di Nyquist è fondamentalmente un grafico di G(jw) dove G(s) e la funzione di trasferimento a ciclo aperto e w è un vettore di frequenze che circondano l'intero semipiano destro. Nel disegnare il diagramma di Nyquist, prendiamo in considerazione sia le frequenze positive che negative (da zero a infinito). Rappresentiamo le frequenze positive in rosso e quelle negative in verde. Il vettore delle frequenze usato per graficare il diagramma di Nyquist di solito è come quello mostrato in figura (immagina che il grafico tende all'infinito):
Se abbiamo poli o zeri sull'asse jw, G(s) non è definita in questi punti, e dobbiamo aggirarli. Il contorno sarà:
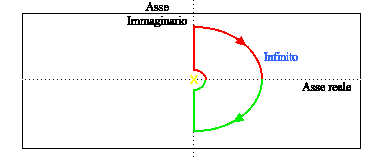
Come già detto, se abbiamo poli sull'asse jw, per avere un grafico corretto dobbiamo usare la funzione da noi definita nyquist1.
Il criterio di Cauchy stabilisce che se prendiamo un curva C chiusa in un piano complesso, e se si mappa attraverso una funzione complessa G(s), il numero di volte che la curva di G(s) gira intorno all'origine è uguale alla differenza tra il numero di zeri e di poli di G(s) inclusi nella zona del piano complesso racchiusa dalla curva C. I giri intorno all'origine sono considerati positivi se seguono la stessa direzione della curva chiusa C, o negativi se le due direzioni sono opposte.
Quando studiamo il sistema retroazionato non siamo interessati a G(s) ma alla funzione di trasferimento a ciclo chiuso:
G(s) --------- 1 + G(s)
Se 1+G(s) circonda l'origine, allora G(s) circonda il punto -1. Ci interessa la stabilità a ciclo chiuso, quindi vogliamo conoscere se ci sono poli a ciclo chiuso (zeri di 1+G(s)) nel semipiano destro. Ulteriori dettagli saranno visti in seguito.
Quindi è molto importante analizzare il diagramma di Nyquist intorno al punto -1 sull'asse reale; la funzione standard nyquist non permette una facile visione di cosa accade intorno a questo punto. Per semplificare l'analisi, possiamo usare una nuova funzione lnyquist1.m che grafica il diagramma di Nyquist usando una scala logaritmica e preserva le caratteristiche del punto -1.
Per vedere un semplice diagramma di Nyquist in Matlab, consideriamo la seguente funzione di trasferimento e disegnamo il grafico:
0.5 ------- s - 0.5
nyquist (0.5,[1 -0.5])
Vediamo ore il diagramma di Nyquist della seguente funzione di trasferimento:
s + 2 ----- s^2
Questa funzione ha un polo nell'origine. Possiamo vedere la differenza dei tre comandi nyquist, nyquist1, e lnyquist1 con questa particolare funzione.
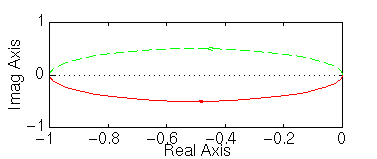
nyquist([1 2], [1 0 0])
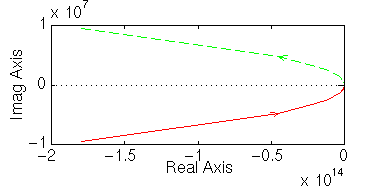
nyquist1([1 2], [1 0 0])
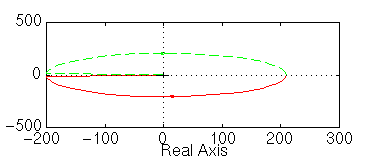
lnyquist1([1 2], [1 0 0])
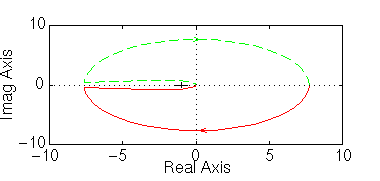
Nota che il grafico con nyquist non è corretto; il grafico tracciato con nyquist1 è corretto ma è difficile vedere cosa accade intorno al punto -1, mentre l'uso della funzione lnyquist1 ci restituisce un grafico corretto e con una scale appropriata.
Consideriamo un sistema con retroazione negativa H(s):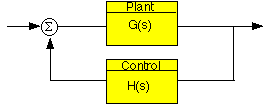 
Dal criterio di Cauchy sappiamo che il numero N di vote che il
grafico di G(s)F(s) gira intorno al punto -1 è uguale alla differenza tra il numero Z di
zeri e il numero P di poli di 1+G(s)H(s) (N = Z - P). Analizzando la funzione di
trasferimento a ciclo aperto e chiuso come numeratore e denominatore, si nota che:
Il criterio di Nyquist stabilisce che:
L'importante equazione che lega queste quantità è:
Z = P + N
Nota: questa è solamente una convenzione per il criterio di Nyquist.
E' molto importante imparare bene come contare il numero di volte che il diagramma gira intorno al punto -1.
Un'altro modo di vedere il problema è di immaginarsi sul punto -1 e di seguire il grafico dall'inizio alla fine. Dobbiamo contare quate volte giriamo di 360° su noi stessi e tener conto del verso (se orario allora N e positivo; se antiorario allora N è negativo).
Conoscendo il numero di poli a ciclo aperto (P) nel semipiano destro (instabili) e il
numero di giri (N), possiamo determinare la stabilità di un sistema a ciclo chiuso. Se Z
= P + N è un numero posistivo diverso da zero il sistema a ciclo chiuso è instabile. Si
può usare il diagramma di Nyquist anche per trovare l'intervallo di guadagno per cui
risulta stabile il sistema a ciclo chiuso con retroazione unitaria.
Esaminiamo il seguente sistema:
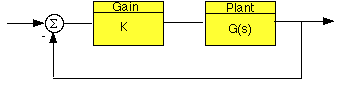
dove G(s) è:
s^2 + 10 s + 24
---------------
s^2 - 8 s + 15
Questo sistema ha un guadagno K che può essere variato per modificare la risposta del sistema. Dobbiamo cercare i valori di K che rendono stabile il sistema a ciclo chiuso. Vedremo che è possibile variare K solo entro certi limiti per essere sicuri che il sistema a ciclo chiuso sia stabile.
La prima cosa è cercare il numero di poli reali positivi nella funzione di trasferimento a ciclo aperto:
roots([1 -8 15]) ans = 5 3
I poli sono entrambi positivi, quindi abbiamo bisogno di 2 giri in senso antiorario (N=-2) del diagramma di Nyquist intorno a -1 per avere un sistema stabile (Z=P+N). Se N< 2 o il verso non è antiorario, allora il sistema è instabile.
Consideriamo il diagramma di Nyquist per K=1:
nyquist([ 1 10 24], [ 1 -8 15])
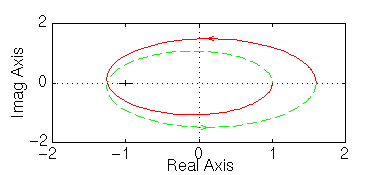
Ci sono due giri in senso antiorario intorno al punto -1, quindi il sistema con guadagno unitario è stabile. Vediamo il comportamento se aumentiamo il guadagno a 20:
nyquist(20*[ 1 10 24], [ 1 -8 15])
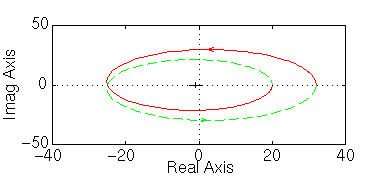
Il diagramma si è allargato, perciò il sistema è stabile qualsiasi sia l'incremento di guadagno. Se il guadagno viene diminuito, il diagramma è contratto e il sistema diventa instabile. Vediamo cosa accade per un guadagno K=0.5:
nyquist(0.5*[ 1 10 24], [ 1 -8 15])
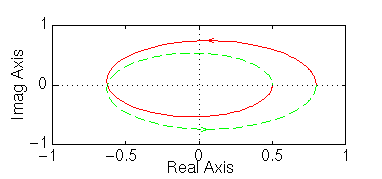
Il sistema è instabile. Eseguedo vari tentativi, troviamo che il sistema diventa instabile per un guadagno K< 0.80.
Nota: Per ingrandire il grafico puoi utilizzare il comando Matlab zoom on e con i tasti del mouse aumentare o diminuire l'ingrandimento.
Se hai dei problemi nel contare i giri intorno al punto -1, prova ad usare la funzione nyquist1 che mostra il numero di giri in senso antiorario (quindi mostra -N) e il numero di poli reali positivi a ciclo chiuso.
Abbiamo già definito il margine di guadagno come la variazione a ciclo aperto del
guadagno (espresso in dB) necessaria affinché, con una fase di -180 gradi, il sistema
diventa instabile. Vediamo da dove deriva quanto detto.
Un sistema è stabile se non ci sono giri intorno al punto -1, così come:
50 ----------------------- s^3 + 9 s^2 + 30 s + 40
Guardando le radici, troviamo che non ci sono poli a ciclo aperto nel semipiano destro, e perciò non ci sono poli a ciclo chiuso se non ci sono giri intorno a -1 nel diagramma di Nyquist.
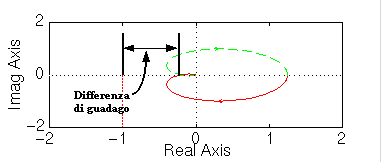
Il sistema a ciclo aperto rappresentato nel grafico diventa instabile a ciclo chiuso se si incrementa il guadagno oltre un certo margine. La distanza, sull'asse reale negativo, tra il punto -1/a (punto dove si ha una fase di 180 gradi, cioè dove il diagramma incrocia l'asse reale) e il punto -1 rappresenta l'incremento di guadagno che può essere tollerato dal sistema a ciclo chiuso prima di diventare instabile.
Deduciamo che se il guadagno è uguale ad "a", il diagramma incrocia l'asse nel punto -1, quindi:
G(jw) = -1/a = a*G(jw) = a* -1/a => a*G(jw) = -1
Passiamo alla notazione in dB:
GM = 20*log10(a) [dB]
Troviamo il margine di guadagno della funzione di trasferimento vista sopra:
50 ----------------------- s^3 + 9 s^2 + 30 s + 40
grafichiamo il diagramma di Nyquist:
nyquist(50, [1 9 30 40 ])
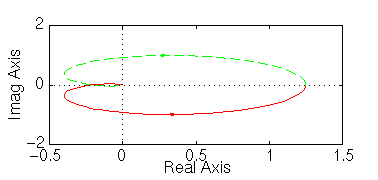
Dobbiamo, come detto, trovare il valore di "a" che è il margine di guadagno cercato. Calcoliamo l'esatto punto di intersezione dell'asse con la curva disegnata. La funzione di trasferimento nel punto 1/a è reale. Il numeratore è reale perciò dobbiamo studiare solo il denominatore. Quando s=jw, i soli termini del denominatore con potenze dispari di s danno un contributo immaginario. Per essere G(jw) reale deve avere:
-j w^3 + 30 j w = 0
Scartata la soluzione banale w=0, la soluzione è data da w=sqrt(30)=5.4772. Dobbiamo trovare il valore della G(jw) nel punto trovato:
polyval(50,j*w)/polyval([1 9 30 40],j*w)
La soluzione è: -0.2174(1/a).
Sappiamo che il margine di guadagno è "a", l'iverso del valore trovato, quindi calcoliamo il margine di guadagno esprimendolo in dB:
-1/a = -0.2174 => a = 4.6 => MG = 20*log10( 4.6) = 13.26 dB
Abbiamo trovato il margine di guadagno. Possiamo verificarlo graficando il diagramma e utilizzando il comando zoom;
a = 4.6 nyquist(a*50,[1 9 30 40])
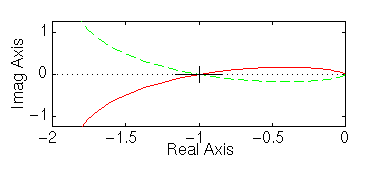
Abbiamo definito il margine di fase come la variazione di fase a ciclo aperto richiesta per rendere il sistema instabile quando il modulo in dB vale 0. Nel disegno è riportata la rappresentazione grafica del concetto espresso sopra.
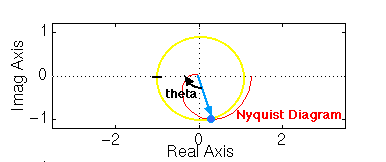
L'angolo Theta rappresemta il margine di fase (in gradi); infatti se Theta è nullo la curva del diagramma incrocia l'asse in -1, quindi il sistema a ciclo chiuso diventa instabile. Per trovale l'angolo Theta si procede disegnando un cerchio unitario centrato nell'origine, misurando l'angolo tra il punto di intersezione del cerchio con la curva e l'asse reale.