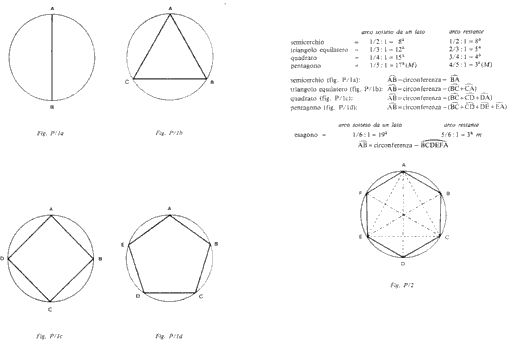
Nel suo Harmonices mundi (Linz, 1619) Giovanni Keplero arriva a dare una base geometrica alla musica.

La divisione di un monocordo viene rappresentata dalla divisione del cerchio mediante l’iscrizione di poligoni regolari.

Confrontando l’arco sotteso da uno dei lati con l’arco restante ottenne esattamente i rapporti di ottava corrispondenti alle prime consonanze armoniche di ottava, quinta, quarta e terza maggiore.

Keplero ottenne anche la sesta maggiore, considerando il rapporto tra l’arco sotteso tra due lati consecutivi di un pentagono e l’arco rimanente.

Moltiplicando i lati dei poligoni, si ottengono poi i sottointervalli:

• passando dal triangolo all’esagono si ottiene la terza minore
• passando dal quadrato all’ottagono si ottiene la sesta minore
  
  
  

Keplero applicò questa sua teoria armonica alla sua teoria cosmologica.
Formulò dunque il noto concetto di musica celestiale, ossia di musica perfetta generata dal moto degli astri. Gli uomini non possono udire questa musica perché ne sono assuefatti fin dalla nascita.
Queste armonie dunque sono per Keplero reali, anche se inudibili.

Vedi all'url: http://www.minerva.unito.it/Storia/PerRagazzi/KepleroMistico.htm