Astrofisica

La formazione delle stelle: LE PROTOSTELLE

Immagine spettacolare della regione centrale della Nebulosa di Orione ripresa dall'HST

PREMESSA

In generale, i modelli di formazione stellare con la conseguente evoluzione verso la Sequenza Principale, sono basati sullo studio dell'evoluzione di una nube di gas freddo (T=10-90 °K), che è una tipica condizione del gas interstellare.
Uno studio dettagliato della formazione stellare, richiede l'analisi dei processi fisici e chimici riguardanti l'interazione tra atomi, grani e fotoni e in piu' la risoluzione dei problemi dinamici per un gas interstellare.

Questi problemi includono l'accelerazione e la decelerazione del gas, con i possibili stati di equilibrio stazionario in cui tutte le forze in gioco si bilanciano. I processi dinamici sono caratterizzati dall'evoluzione temporale delle quantità v (velocità macroscopica del sistema) e B (campo magnetico). La trattazione matematica, che prevede la risoluzione delle equazioni differenziali, che non tratteremo in questo contesto, anche se semplificate, porta lo stesso a risultati importanti con semplici modelli teorici.
Possiamo così seguire l'evoluzione di una protostella, attraverso le diverse fasi di contrazione ed espansione, verso la sequenza principale. I processi chimici e dinamici che analizzeremo, permettono di intuire come essi dipendano dalla perdita di massa, cioè di energia, da parte della protostella.
Infatti, una protostella si avvicina alla sequenza principale, seguendo tracce evolutive diverse a seconda della sua massa. Quindi, ciò che accade durante la prima fase dell'evoluzione stellare, è molto importante per poter definire le caratteristiche delle stelle di sequenza principale.
Inoltre, i processi chimici e fisici sono importanti perché tramite essi la stella interagisce con il mezzo interstellare favorendo la formazione di nuove stelle.
In questo articolo, si vuole dare una idea generale sulla formazione stellare e sugli stadi che seguono la formazione iniziale fino alla sequenza principale, facendo una analisi semplificata della contrazione di una nube distribuita con simmetria sferica e che si contrae conservando tale distribuzione. Per fare ciò, analizzeremo le condizioni sotto le quali una nube di gas interstellare si trova in equilibrio termico e dinamico, che diventeranno le condizioni al contorno del nostro problema. Infine, tratteremo la frammentazione delle nubi interstellari che è all'origine degli ammassi aperti e degli ammassi globulari, e il collasso in presenza di un campo magnetico.

LO STATO DI UN FLUIDO INTERSTELLARE

In condizioni interstellari una nube è caratterizzata da alcune quantità alla cui variazione temporale è spaziale sono associati stati di equilibrio e non della nube di gas. Per analizzare le variazioni di queste quantità che sono, ρ (densità della nube), V (potenziale dovuto a masse interne e/o esterne alla nube),v (velocità macroscopica del sistema), B (campo magnetico) e P (pressione del gas), bisogna determinare un insieme di equazioni differenziali la cui risoluzione ci permette di conoscere, a partire da una condizione iniziale, lo stato di una distribuzione di gas.
L'analisi qualitativa di questo insieme di equazioni, porta ad alcuni risultati importanti relativi alla dinamica del problema.
Il comportamento macroscopico è descritto dalla variazione temporale e spaziale della velocità macroscopica del sistema, la quale è definita come la media delle velocità delle particelle contenute in un piccolo volume integrata poi su tutto il volume che contiene il gas. Una conseguenza importante è che se la velocità macrospica del fluido v=0, allora il tempo richiesto per la variazione di B è dell'ordine di 4vL, dove L è la scala di distanza del campo magnetico. Se L=1 U.A. (Unità Astronomica"1.5x10^13 cm), allora il tempo richiesto è dell'ordine di circa 10^9 anni per la tipica conduttività interstellare.

Come si può constatare questo tempo è molto alto, per cui per L grande il campo rimane costante anche relativamente all'età dell'universo. Se invece si è in presenza di materiale in moto ed L è molto piccola, allora il flusso magnetico attraverso il "circuito" che segue il fluido è costante. In questo caso le linee di forza del campo magnetico seguono il fluido in moto, perciò si dice che sono "congelate". Quando il fluido è soggetto a piccole perturbazioni attorno alla posizione di equilibrio, espressa dal "Teorema del Viriale", queste considerazioni ci consentono di analizzare i modi con cui si propagano le onde in un fluido.

IL TEOREMA DEL VIRIALE

In base alle precedenti considerazioni, è facile intuire che per studiare la dinamica di un fluido bisogna conoscere in dettaglio lo stato di equilibrio del gas interstellare. La condizione di equilibrio è data dal Teorema del Viriale, che in forma matematica, nel caso piu' semplice, cioè in presenza di un potenziale gravitazionale V dovuto solo alla distribuzione di gas e dell'energia cinetica T del sistema, è espresso dalla relazione:

2T+V=0

Se supponiamo che la velocità macroscopica del sistema sia nulla, ciò implica che l'energia T è costante, da cui si ricava che non vi è variazione del potenziale gravitazionale, perciò il sistema è in equilibrio. Per essere piu' precisi, bisogna tenere conto del fatto che considerato un sistema di riferimento inerziale, la nube rispetto ad esso può traslare e ruotare, quindi, l'energia cinetica contiene anche il contributo dovuto alla rotazione che produce una forza centrifuga che si oppone alla contrazione. Queste semplici considerazioni valgono se la nube è isolata e non c'è campo magnetico. È facile intuire che gli effetti di quest'ultimo complicano la forma del viriale e l'analisi che ne consegue.
L'equilibrio termico e dinamico di una nube di gas interstellare, è un importante punto di partenza per l'analisi del collasso gravitazionale. E' necessario, quindi, fare un'analisi qualitativa del problema in modo da capire quali sono le condizioni al contorno da cui partire per produrre il collasso gravitazionale di una nube di gas interstellare.

L’EQUILIBRIO DELLE NUBI INTERSTELLARI

Essenzialmente, possiamo affermare che il moto del gas tende a produrre una pressione di equilibrio nel senso che il gradiente di pressione tra le varie regioni della nube si oppone (bilanciandola) alla forza gravitazionale. Ciò produce espansione nelle regioni con alta pressione e contrazione nelle regioni con bassa pressione.
Rispetto al valore medio della nube, le differenze di pressione fra le varie regioni sono prodotte da fonti di energia come le stelle giovani all'interno della nube o le esplosioni delle supernovae. Per esempio, considerando che per annullare le differenze di pressione in una regione è necessario il tempo che il suono impiega per attraversare le regione stessa, ci si aspetta che le regioni diffuse di HI, con estensioni di 5 pc (parsec), raggiungano una pressione di equilibrio rispetto alla regione circostante in circa 7x10^6 anni.
Confrontando questo tempo con quello di collisione tre due nubi, t=1.2x10^7 anni, si può concludere che le nubi interstellari raggiungano solo parzialmente la pressione di equilibrio. Le osservazioni sono in buon accordo con le previsioni teoriche.

Infatti, considerando l'equazione dei gas perfetti, in condizioni interstellari per le regioni di HII con T= 80 °K, rho=3x10^-24 g/cm^3, nH=20/cm^3, si ottiene una pressione di equilibrio Pe=2.6x10^-15 dine/cm^2. Quindi, alcune nubi diffuse si troveranno a basse pressioni, altre saranno caratterizzate da alte pressioni, soprattutto quelle compresse dal passaggio di onde d'urto provocate dalle esplosioni delle supernovae o da regioni di HII in espansione. Nelle regioni estese di gas ionizzato la pressione può non essere molto diversa da Pe, anche se vi sono delle incertezze. Infatti, in generale, in una regione di HII a 8000 °K il corrispondente valore di nH, consistente con il valore di Pe, prendendo 2.1 particelle libere per atomo di H al posto di 1.1 per le regioni di HI, è 0.11/cm^3. Questi valori sono consistenti sia con quelli osservati sia con il valore della densità elettronica Ne=0.03/cm^3 ottenuto dalla misura della dispersione delle pulsar. La pressione per le regioni di HII che risulta usando questi valori, è circa 3 volte maggiore di Pe ed è consistente con una espansione dinamica.

EQUILIBRIO DI UNA NUBE DI GAS SFERICA

Se consideriamo una nube di gas distribuita in una sfera, il teorema del viriale, sotto precise condizioni, metterà in relazione la pressione con l’energia gravitazionale e fornirà una condizione che deve essere soddisfatta all’equilibrio.

Ignorando la presenza di masse esterne alla nube, si può considerare solo l’energia potenziale gravitazionale totale del sistema, che per una sfera di densità uniforme e raggio R assume, approssimativamente, il valore GM/5R.

Se R è sufficientemente grande allora il termine gravitazionale può essere trascurato, perciò la pressione interna ed esterna alla nube si bilanciano.

Se, invece, la pressione esterna aumenta R diminuisce, per cui il termine gravitazionale diventa sempre piu’ grande favorendo la contrazione. Quando il termine gravitazionale diventa molto grande da favorire un ulteriore decremento di R, bisogna che la pressione esterna diminuisca poiché non sono possibili soluzioni con Po che aumenta ancora.

Nel caso considerato, sono stati trascurati gli effetti dovuti alla presenza di un campo magnetico. Si può dimostrare che il campo magnetico di una nube in collasso, rimane congelato con la nube contribuendo al collasso, in quanto le forze magnetiche non riuscendo ad arrestare il collasso nelle prime fasi, esse non vi riusciranno neanche in seguito.

Chandresseckar ha dimostrato che in presenza di una rotazione uniforme o di un campo magnetico uniforme, o entrambi, il criterio di JEANS vale ancora nel senso che le perturbazioni di densità, che si propagano con una certa lunghezza d’onda producono una instabilità gravitazionale se quest’ultima è maggiore di un certo valore detto lunghezza d’onda di JEANS.

Analizzeremo ora la contrazione a simmetria sferica di una nube di gas di massa Mn, raggio Rn e densità rn. Questo ci permetterà di capire, in linea generale, quali sono le condizioni fisiche all’interno di una distribuzione di gas in contrazione e quale è la dinamica del processo.

MODELLO PER UNA NUBE IN COLLASSO GRAVITAZIONALE

La presenza di un campo magnetico complica sia fisicamente che matematicamente la dinamica per una nube in equilibrio termodinamico soggetta a collasso gravitazionale a seguito dell’instabilità che può nascere se la nube ha una massa maggiore di un certo valore.

Consideriamo inizialmente che il campo magnetico della nube sia nullo. Questa condizione non è una condizione reale, ma poiché il criterio di JEANS è valido, questo ci permette di semplificare il problema.

Se la massa è distribuita a simmetria sferica, non sono presenti rotazioni e se la densità è uniforme allora si ha

M_n=4/3pR_n³r_n

dove

M_n=MASSA DELLA NUBE

R_n=RAGGIO DELLA NUBE

r_n=DENSITA’ DELLA NUBE

Mentre la pressione è data dalla formula P_G=r_nKT_n/m che è l’equazione per una gas alla temperatura T e peso molecolare m. Queste due semplici equazioni consentono di ricavare una semplice relazione che lega la pressione al raggio:

P_Gµ1/R_n³.

Questo implica che quando la nube si contrae si stabilisce un gradiente di pressione e quest’ultima aumenta rapidamente andando verso il centro. Per capire quale importanza ha questo fatto nel collasso bisogna analizzare il problema piu’ in dettaglio.

Nel nostro caso abbiamo supposto che la nube non sia influenzata gravitazionalmente o radiativamente da masse esterne o interne, quindi il sistema si dice isolato. Ne consegue che il potenziale F è uguale al potenziale gravitazionale totale. Inoltre, la pressione P è data solamente dalla pressione del gas. Partendo, quindi, dalla condizione di equilibrio, caratterizzata da una pressione iniziale P_o, densità inziale r_o, raggio iniziale R_o, perturbiamo la nube considerando onde di densità che si propagano al suo interno con una certa frequenza. Come dicevamo precedentemente la causa di queste onde può essere individuata nelle esplosioni delle supernove, nelle interazioni gravitazionali tra galassie etcc….

Poiché il nostro problema è unidimensionale, essendo il collasso a simmetria sferica, bisogna considerare variazioni solo lungo il raggio.

Quando la nube è perturbata, nel senso che la sua densità varia sia nel tempo che spazialmente, si crea un’instabilità di tipo gravitazionale e la nube comincia a contrarsi seguendo la legge del moto

F=ma.

Possiamo cosi analizzare gli stati dinamici che caratterizzano una nube in collasso. Come vedremo il problema sarà caratterizzato dai cosiddetti “tempi dinamici” del processo che ci diranno se la nube è in contrazione o no. Infatti, la soluzione dell’equazione del moto ci porta a calcolare il tempo t_ff di caduta libera e t_ef tempo di espansione dinamico.

Il confronto di questi due tempi, essendo essi legati strettamente al valore della densità della nube, alla temperatura e alla velocità di contrazione confrontata con la velocità del suono, permette di affermare che se t_efè maggiore di t_ff siamo nella fase di contrazione, mentre se è t_ff maggiore di t_ef siamo nella fase di espansione. Nel caso questi due tempi siano uguali, allora la nube sta attraversando una fase di equilibrio.

Dobbiamo quindi immaginare uno scenario in cui i processi di contrazione ed espansione della nube si verifichino con una velocità supersonica. Infatti, dall’analisi dei tempi dinamici, si deduce che la variazione del raggio che determina la velocità di contrazione o espansione (ricordarsi che il raggio è uno spazio, quindi la variazione di uno spazio rispetto al tempo è una velocità), è maggiore della velocità del suono (che dipende dalla variazione della pressione rispetto alla densità) all’interno della nube.

Un’ analisi ancora piu’ approfondita deve tenere conto oltre che degli aspetti puramente dinamici, anche degli aspetti termodinamici con tutte le conseguenze che ne derivano. Infatti, la temperatura e la densità della protostella dipendono dal tasso di raffreddamento o riscaldamento oltre che dalla espansione e dalla contrazione del gas.

TEMPO SCALA DI RAFFREDDAMENTO E DI RISCALDAMENTO

Consideriamo il caso di una protostella ancora debole, cioè che emette poca radiazione, in grado di confinare quest’ultima al suo interno in quanto sufficientemente densa.

Indichiamo con L il tasso di perdita di energia per unità di volume dovuta alla radiazione emessa dai grani, dagli atomi e dalle molecole. Sia G il guadagno di energia, che contiene il contributo dovuto alla radiazione prodotta dalla protostella che viene assorbita interamente dagli atomi e dalle molecole, e il contributo dovuto all’interazione tra la radiazione interstellare e i grani.

Se il tasso di perdita di energia è maggiore del guadagno, si ha un raffreddamento della stella con un tempo scala t_rafµ(L-G), mentre se si verifica la situazione opposta si ha un tempo scala di riscaldamento t_risµ(G-L). Quando stella è debole e densa da confinare la radiazione da essa stessa prodotta, la perdita di energia è dovuta soltanto alla diffusione dei fotoni al suo interno. Di conseguenza si ha un flusso di energia uscente che è proporzionale alla variazione di temperatura rispetto al raggio. Si ricava che il tempo di raffreddamento dipende sicuramente dal flusso uscente che ne determina il valore. In particolare, i tempi scala di raffreddamento e riscaldamento possono essere calcolati in funzione della densità e temperatura e confrontati con quelli di espansione e contrazione per una stella di data massa e composizione chimica.

Usando questi risultati si può produrre un diagramma densità-temperatura per l’evoluzione di una protostella, di data massa, in un intervallo si temperatura da 1-1000 °K e di densità da 10²³-10¹² gm/cm³. Si possono tracciare i lineamenti evolutivi, tenendo presente che per stelle di massa maggiore di 10^-2 M_{o (masse solari)} la curva t_raf= t_ff si trova vicino alla linea di equilibrio t_ef=t_ff.

Come si può vedere nella figura, nella regione attorno alle curve t_raf= t_ff e t_raf= t_ef_, il raffreddamento è piu’ veloce dell’espansione o contrazione, perciò l’evoluzione procede verticalmente.

D’altra parte, nella regione t_ris= t_ff e t_ris= t_ef, il riscaldamento è piu’ veloce dell’espansione o contrazione. Quindi, le condizioni di equilibrio idrostatico non sono necessariamente soddisfatte quando la stella si trova nella regione della linea di equilibrio.

Primo perché la stabilità che si oppone al moto adiabatico della protostella fuori dalla linea di equilibrio richiede che g>4/3 (esponente adiabatico nell’equazione di stato del gas).

Così la stella può essere sempre in quasi-equilibrio idrostatico se la sua densità e temperatura media sono valori che si trovano nella zona di ionizzazione dell’atomo di idrogeno e nella zona di dissociazione per la molecola di H₂.

Secondo, il tempo scala di raffreddamento o riscaldamento come abbiamo visto possono essere maggiori di t_{ff .} tutto ciò è importante per la definizione di quasi-equilibrio idrostatico. Quindi, per trovare i lineamenti evolutivi di una protostella è necessario conoscere G e L in ogni punto del diagramma densità-temperatura.

Consideriamo la regione sufficientemente vicino alla linea di equilibrio t_ef= t_ff. E’ importante notare che la direzione di una linea evolutiva è orizzontale quando essa attraversa la curva t_raf= t_ff e t_ris= t_ef . come mostrano le curve tratteggiate nella figura 1, se una stella nasce con una densità uguale a quella del punto P, essa si avvicina alla curva t_ris= t_ef senza ritorno alla temperatura iniziale. D’altra parte, una stella nata con densità tra il punto A e il punto P si avvicina alla linea che parte dal punto A. l’evoluzione dopo il punto A, dove la stella diventa opaca, è una contrazione in caduta libera quasi adiabatica.

In un certo senso, il punto A può essere visto come uno stato iniziale per una stella opaca che è indipendente dal suo passato.

Nelle sezioni che seguono ci occuperemo delle stelle opache, analizzando in dettaglio questi stadi evolutivi. Vedremo che certi lineamenti evolutivi sono uguali a tutte le stelle con massa maggiore di 10^-2 M_o per le quali il punto A si trova attorno alla linea di equilibrio.

PROCESSI DI RISCALDAMENTO E RAFFREDDAMENTO NELLE PROTOSTELLE

Questi processi devono essere studiati in due casi, che riguardano le stelle trasparenti o opache alla radiazione interstellare e stellare.

Analizzeremo questi due casi confrontando i tempi caratteristici di questi processi con i tempi di caduta libera o espansione. Ciò ci darà delle indicazioni importanti sulla evoluzione della protostella.

Infatti, questa si evolverà a seconda dello stato in cui si trova. Lo stato può essere trasparente o opaco, per cui la stella, che cercherà di raggiungere l’equilibrio, si riscalderà o si raffredderà in modo da sopravvivere al collasso o alla esplosione.

Stadi trasparenti:

le molecole che producono un efficiente riscaldamento della protostella sono quelle di idrogeno che emettono radiazione a circa 28 micron (IR).

Poi, ci sono i grani che emettono radiazione termica. Infine, gli ioni come C⁺, Si⁺ ,Fe⁺, che emettono per eccitazione dovuta ad impatto con un elettrone. Bisogna tenere conto anche dei raggi cosmici che ionizzano gli atomi e le molecole.

Essenzialmente, in una analisi dettagliata il processo di collisione tra elettroni e atomi può essere trascurato, primo perché il tasso di interazione è basso, secondo perché quando la stella è opaca alla radiazione interstellare questo processo è inefficiente.

Idrogeno molecolare:

a basse temperature, circa 150 °K, la maggior parte delle molecole di H si trova nello stato rotazionale J=0. la principale eccitazione è lo stato J=2 sia per atomi di idrogeno che per le molecole con energia di eccitazione di 0.044 eV. Questo stato è diseccitato parzialmente dalle collisioni con particelle e parzialmente con emissione di fotoni a 28 micron. Cercherò, ora, di rendere l’idea di cosa succede senza l’uso di particolari equazioni, ma facendo riferimento a quelle che sono le quantità fisiche in gioco nei porcessi che stiamo descrivendo.

A temperature di circa 150 °K, il contributo dei livelli alti rotazionali non può essere trascurato. Assumeremo, quindi, che per gli stadi trasparenti la concentrazione di idrogeno è:

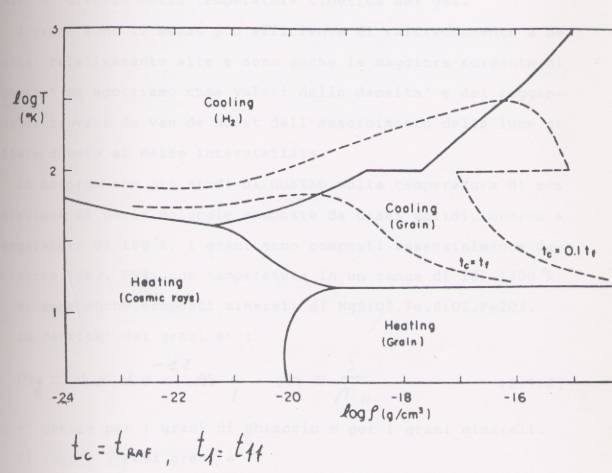
n_H2= n_H_.

A basse densità il contributo al processo di raffreddamento dovuto alle molecole di idrogeno, supera quello dovuto ai grani. Il caso inverso succede quando una stella è opaca alla radiazione interstellare. Questo fa si che le molecole di idrogeno non giochino un ruolo determinante per raggiungere il punto critico A, dove la densità dei grani è più piccola di 10^-13 n_H2_. (Fig. 1)

Fig. 1- Confronto dei processi di riscaldamento e di raffreddamento per stelle completamente trasparenti alla radiazione interstellare. Le curve continue rappresentano i bordi delle regioni dove ognuno dei quattro processi è predominante. (Cooling=Raffreddamento; Heating=Riscaldamento).

Grani

A basse temperature la maggior parte degli elementi sono condensati sotto forma di grani come nel mezzo interstellare. Questi grani hanno temperature attorno ai 20 °K, che, in generale, è diversa dalla temperatura cinetica del gas.

I grani sono il mezzo più efficiente di raffreddamento a densità relativamente alte e sono anche la maggior sorgente di opacità se adottiamo come valori della densità e del raggio quelli trovati da Van de Hulst dall’assorbimento della luce stellare dovuto al mezzo interstellare.

In accordo con gli studi di GUSTAD sulla temperatura di evaporazione di varie molecole composte da grani solidi, intorno a temperature di 100 °K, i grani sono composti essenzialmente da ghiaccio, NH2, CH4, con temperature in un range di 100-1300 °K. Vi sono anche composti di MgSiO3, Fe, SiO2, Fe2O3.

Raggi Cosmici

Per quanto riguarda i raggi cosmici, questi, interagendo con le particelle, producono un riscaldamento il cui rate diventa un contributo importante quando si è a densità di 10^-18 g/cm³.

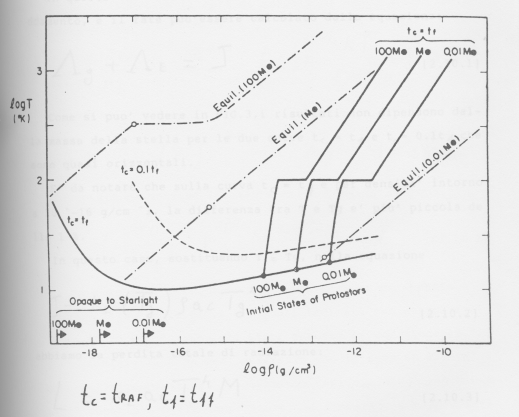
CONFRONTO DEL RATE DI RAFFREDDAMENTO, DI RISCALDAMENTO E DI CADUTA LIBERA

Quando una stella è completamente trasparente alla radiazione interstellare, il rate di raffreddamento e quello di riscaldamento dipendono soltanto dalla densità e dalla temperatura e non dalla massa della stella.

La temperatura dei grani, come abbiamo visto è di circa 15 °K. Il tempo di caduta libera, invece, dipende solo dalla densità. Nella fig.1 sono confrontati il tasso di riscaldamento, di raffreddamento e di caduta libera nel diagramma T-r.

Il diagramma è diviso in quattro regioni che, essenzialmente, indicano le zone in cui uno dei quattro processi domina sugli altri. Questi processi non sono scambi di energia sul bordo che delimita le regioni di raffreddamento o riscaldamento.

Ora, per una setlla di una massa solare, si trova che la linea di equilibrio te=tf passa attraverso la regione di raffreddamento dei grani e non attraverso la regione di raffreddamento delle molecole di H2. Così, per quelle stelle non è importante studiare il loro passato, sempre che la concentrazione degli atomi di idrogeno è confrontabile con la concentrazione degli atomi di H, come è stato assunto nel disegnare la figura 1.

Si può quindi vedere che ad alte densità il rate di riscaldamento, che dipende dal quadrato della densità, è più importante del contributo dovuto ai raggi cosmici.

Consideriamo una stella opaca alla radiazione interstellare, ma con densità così bassa da risultare trasparente alla radiazione termica emessa per la maggior parte dai grani. Le densità intorno alle quali una stella è opaca alla luce interstellare sono mostrate in figura 2 dalle linee e dai cerchi (neri e bianchi) per stelle di 10^-2 Mo, 1 Mo, 10² Mo.

Fig. 2 – Confronto tra il tempo-scala di raffreddamento e quello di caduta libera per stelle opache alla radiazione interstellare. Le curve tratteggiate col punto rappresentano lo stato di equilibrio gravitazionale con indice politropico uguale a 3. sia i cerchi neri che quelli bianchi rappresentano lo stato in cui lo spessore ottico per la radiazione termica è uguale al raggio stellare.

In questo caso domina il contributo dei grani per il raffreddamento ed i risultati non dipendono dalla massa della stella per le curve tc=tf e tc=0.1tf che sono quasi orizzontali.

E’ da notare che la curva tc=tf per densità intorno a 10^-16 g/cm³, la differenza tra T e Tg è più piccola dell’ 1%. Se nella figura 2 si sostituisce 10^-14 al posto di ng/n=10^-13 , allora la curva tc=tf coincide con la curva tc=0.1tf. questo significa che la curva tc=tf non risente molto dal numero di grani nella regione di alta densità.

CONTRAZIONE DINAMICA

Nel diagramma densità-temperatura l’evoluzione di una stella opaca può essere analizzata partendo dallo dallo stato inziale descritto dal punto A (vedi astroemagazine n° 12).

Quando la densità aumenta, la contrazione della stella può essere vista come una caduta libera adiabatica (vedi figura 3).

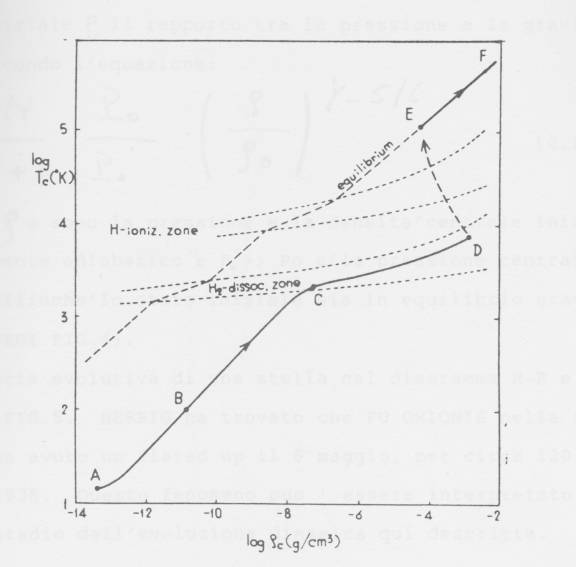
Fig. 3 – Variazione della densità e temperatura centrale per una stella opaca di 1 Mo. Il punto A rappresenta lo stato inziale. Il punto C e il punto D, rappresentano lo stato di rimbalzo del core e la linea DE indica la fase di riscaldamento rapido. Il punto E indica lo stato di quasi-idrostatica contrazione,mentre le linee tratteggiate rappresentano lo stato di equilibrio di indice politropico 3/2.

La figura 3 si riferisce alla variazione della densità e della temperatura centrale (rhoc e Tc), assumendo che inizialmente tutto l’idrogeno era sotto forma di molecole che hanno alta densità.

La linea BCD è sufficientemente in accordo con la linea EF che rappresenta l’equilibrio gravitazione per indice politropico 3/2.

Se la densità diminuisce andando verso l’esterno, le shells (strati) più in alto tendono a contrarre le altre. Ciò implica che sotto le condizioni di adiabaticità l’aumento della pressione al centro è molto rapido. Quando la contrazione procede fino ad un certo limite, il contributo gravitazionale nella regione centrale diventa confrontabile o minore del contributo dovuto alla pressione; il risultato è un rimbalzo del core.

La traccia evolutiva di una stella nel diagramma H-R è illustrata nella figura che segue.

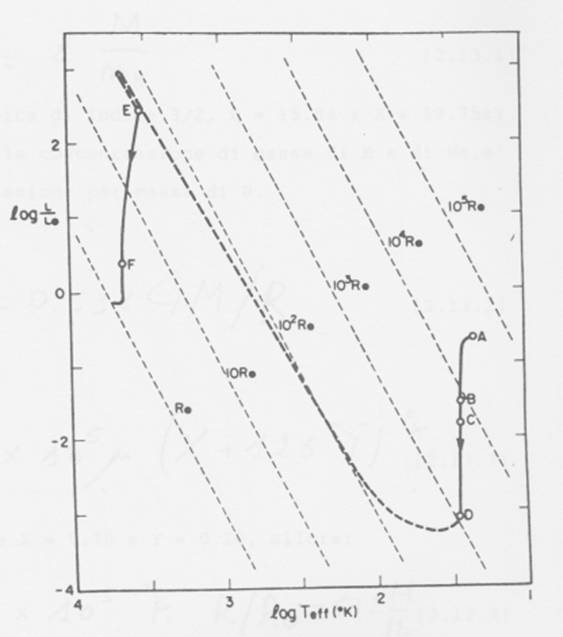
Fig 4 – Traccia evolutiva di una stella di una massa solare, nel diagramma H-R, opaca. I punti da A ad E sono gli stessi della figura 3. La linea EF indica lo stadio di contrazione quasi idrostatica verso la sequenza principale.

Herbig ha trovato che FU Orionis nella regione HI ha avuto un flare-up (aumento improvviso di luminosità) il 6 maggio, per circa 120 giorni, nel 1936. Questo fenomeno può essere interpretato come l’ultimo stadio dell’evoluzione dinamica qui descritta.

CONTRAZIONE QUASI-IDROSTATICA ED EVOLUZIONE VERSO LA MAIN-SEQUENCE

Il flare-up di una stella è seguito da una fase di transizione. In questa fase l’energia del moto di massa è dissipata sotto forma di energia termica, con l’entropia che si avvicina a quella di uno stato di quasi-equilibrio idrostatico.

Il tempo scala di questa transizione sta in un intervallo di 0.1-100 anni per una stella di 1 Mo. Dopo la stella si stabilisce sulla linea EF della figura 4 contraendosi in quasi-equilibrio idrostatico.

L’energia totale di questo stadio è uguale alla energia spesa per dissociare le molecole di H e ionizzare gli atomi di idrogeno e di elio.

Il punto E nelle figure 3-4 e i cerchi bianchi in figura 6 corrispondono a questi valori. L’evoluzione della stella può essere analizzata nella figura 5.

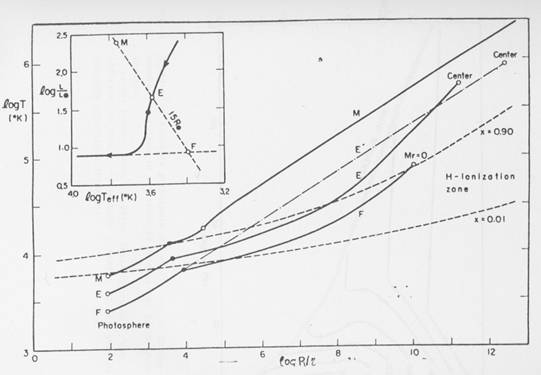
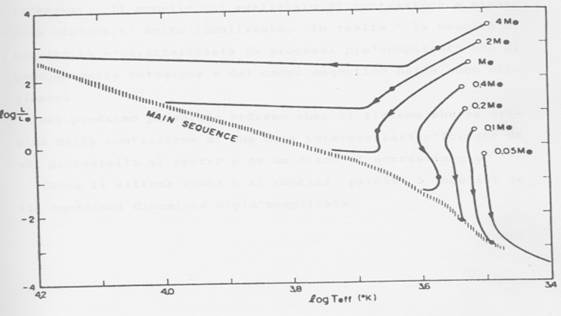
Fig. 5 –Variazione della densità e della temperatura in una stella di una massa solare basata su un modello con opacità costante. I cerchi neri indicano i punti del gradiente di temperatura adiabatico, mentre i cerchi bianchi sulla curva M indicano il bordo superiore della regione convettiva (HAYASHI)

La contrazione quasi-idrostatica di una stella, continua finchè la protostella non raggiunge la sequenza principale dove la temperatura centrale è così alta da innescare l’idrogeno.

L’entrata in sequenza principale di stelle con masse diverse può essere analizzata in figura 6.

Fig. 6 – Entrata in sequenza principale di stelle che in pre-sequence si trovano in uno stato di contrazione quasi-idrostatica. I cerchi bianchi sono lo stato iniziale, qualli neri indicano lo stadio convettivo o stadio di età zero di sequenza principale.

Dal punto di vista dinamico, quindi, l’evoluzione verso la sequenza principale di una protostella, è caratterizzata da diverse fasi di contrazione ed espansione adiabatica che dipendono dalla temperatura interna e dalla luminosità emessa. Il modello qui analizzato, di contrazione a simmetria sferica, è molto idealizzato. In realtà la nascita di una stella è caratterizzata da processi più complicati che dipendono dalla rotazione e dal campo magnetico della nube originaria.