.: CURVA: APPROFONDIMENTI :.

GLI SPECCHI USTORI

Come detto in precedenza il cerchio è un'ellisse con i fuochi coincidenti; nell'ellisse i due fuochi sono sempre più lontani man mano che questa si allunga fino a diventare una parabola in cui si ha un solo fuoco (l'altro, per così dire, è andato all'infinito). I raggi che provengono da questo fuoco all'infinito sono delle rette parallele, che riflettendosi sulla parabola vanno a finire nel fuoco effettivo. Se dunque vogliamo concentrare in un punto dei raggi paralleli (o praticamente paralleli, come ad esempio quelli del Sole) si dovrà usare uno specchio a forma di parabola o, meglio, di paraboloide. Il paraboloide è una superficie generata dalla rotazione di una parabola sul proprio asse. Se si taglia la superficie del paraboloide con piani perpendicolari all'asse si ottengono solo circonferenze; se si interseca con piani paralleli all'asse si ottengono solo parabole uguali o simili a quella dalla cui rotazione è stato generato il paraboloide. Così facendo si può costruire uno specchio ustorio, capace di incendiare un pezzo di carta o di legno posto nel suo fuoco.

La leggenda secondo la quale Archimede (III sec. a.C.) avrebbe incendiato le navi romane con uno specchio ustorio ha dato luogo ad un numero considerevole di ricerche in questo senso fino al Seicento inoltrato.

il calore emesso da una lampadina posta nel fuoco di uno degli specchi riesce a far accendere un fiammifero posto nel fuoco dell'altro specchio.

Anche i fari delle automobili e i proiettori utilizzano specchi a forma di paraboloide per ottenere una migliore distribuzione del fascio luminoso.

ANTENNE PARABOLICHE

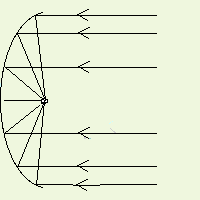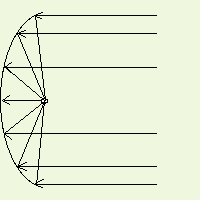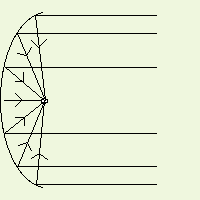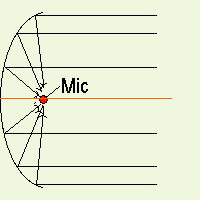
La parabola fornisce un eccellente modo per concentrare i suoni provenienti da una particolare posizione e allo stesso tempo attenuare tutti gli altri suoni. Nella parabola, tutte le onde sonore parallele al suo asse vengono riflesse in un unico punto detto fuoco.  Ponendo un piccolo microfono proprio in questo punto si riceverà tutta l'energia che colpisce il piatto della parabola.  Notare che senza la parabola, questo microfono riceverebbe solo una piccola parte dell'energia emanata dalla sorgente sonora e, ciò che è peggio, riceverebbe anche altri suoni indesiderati provenienti da altre direzioni, rendendo quasi impossibile isolare ed udire il suono o la conversazione desiderati. Se si pone un microfono nel fuoco di una parabola con  piatto di circa 50 cm di diametro la situazione è ben diversa. La superficie che riceve le onde sonore è infatti circa 5000 volte maggiore di quella che offre il microfono da solo. In tal modo, anche la quantità di energia sonora che colpisce il microfono viene incrementata di 5000 volte, e cosa ancora più apprezzabile, saranno ricevuti solo i suoni desiderati, cioè quelli provenienti da una certa direzione

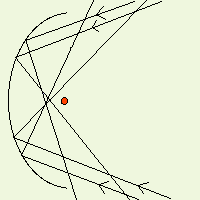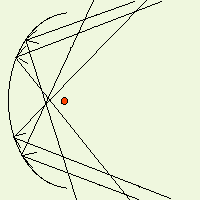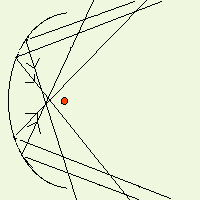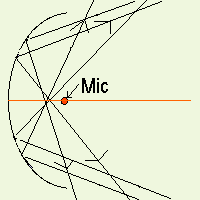
In questo esempio, l'onda sonora arriva con un certo angolo  e non è quindi allineata all'asse della parabola.  Notare che tutte le onde sonore che colpiscono il piatto della parabola vengono indirizzate altrove e non finiscono sul microfono!  Solo le onde allineate con l'asse della parabola finiranno sul microfono posizionato nel fuoco.

Sullo stesso principio ovviamente si basano le parabole satellitari poste sui tetti delle nostre case: non si tratta più di onde sonore, ma magnetiche; non c'e più il microfono ma un apposito convertitore posto nel fuoco.

Passiamo ora a esaminare l'ultima tra le coniche, l' iperbole , che è anche la più complessa di tutte. Consideriamo il solito piano, ma stavolta lo incliniamo ancore di più che la retta generatrice, la curva ottenuta, oltre ad estendersi all'infinito, presenta una nuova proprietà: è formata da due rami staccati fra loro .

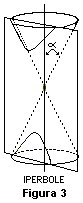
L'iperbole può essere definita come il luogo geometrico dei punti del piano per i quali è costante la differenza delle distanze da due punti fissi detti fuochi . Considerando uno specchi iperbolico (bisogna considerare entrambi i rami dell'iperbole) emettiamo da uno dei due fuochi un raggio di luce, il raggio riflesso starà sulla congiungente l'altro fuoco con il punto di riflessione.

Nel "Dialogo intorno a Due Nuove Scienze" , Galileo affronta il problema del moto dei proiettili. Prima di Galileo, si credeva che un corpo lanciato in direzione orizzontale, per esempio un proiettile sparato da un cannone, si muovesse in direzione orizzontale fino ricadeva verso terra, seguendo una traiettoria curvilinea che però non era ancora conosciuta.
Galileo si accorse, durante lo studio del moto dei proiettili, che essi non sono soggetti soltanto alla forza che li spinge in direzione orizzontale, ma anche alla forza di gravità, il moto deriva quindi dalla somma vettoriale di due componenti.

La prima componente e data da un moto uniforme, il corpo ad essa soggetto percorre una distanza in orizzontale che e' proporzionale al tempo impiegato per percorrerla. La seconda invece provoca un moto uniformemente accelerato, cioè la distanza percorsa in verticale e' proporzionale al quadrato del tempo impiegato a percorrerla. Galileo dimostrò che la combinazione dei due moti orizzontale e verticale da come risultato il moto del proiettile lungo un arco di parabola.

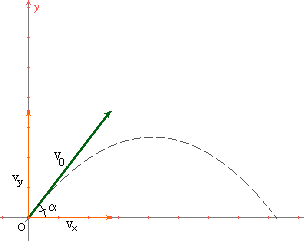
Tenendo come riferimento la figura a lato, vogliamo ricavare, utilizzando la legge di caduta, la traiettoria di un proiettile verificando che è una parabola e mostrandone poi alcune caratteristiche.

Terremo conto solo delle forze gravitazionali, supponendo nulla l'influenza dei vari agenti atmosferici, in particolare le forze di attrito dell'aria e  quelle del vento.

Le leggi della cinematica che esprimono la posizione del proiettile nel piano al tempo t con

g : accelerazione di gravità
v o : velocità iniziale,
a: angolo formato dalla bocca da fuoco col terreno ( alzo )

avendo assunto x 0 =0 e y 0 =0

sono espresse dalle seguenti formule:

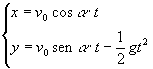
x = 1/2at 2 + v 0 t

risolvendo la prima rispetto alla t e sostituendo nella seconda si ottiene l'equazione della traiettoria, che rappresenta una parabola passante per l'origine:

intersecando con l'asse delle x, cioè sostituendo y=0 nella precedente si ottiene la gittata:

LA CICLOIDE

la curva descritta da un punto P di una circonferenza che rotoli senza strisciare su una retta. Una cicloide si dice ordinaria, accorciata, allungata a seconda che P giaccia sulla circonferenza, sia interno o esterno. La cicloide rappresenta quindi la traiettoria di un punto di una circonferenza che rotola nel piano lungo una retta fissa senza strisciare; è una curva periodica, in quanto a ogni giro della circonferenza si ripete uguale a sé stessa. Ha una proprietà molto interessante: se consideriamo due punti non alla stessa altezza, qual è la traiettoria che un oggetto deve percorrere per arrivare da un punto all'altro nel minor tempo possibile se è mosso solo dalla forza di gravità? Una prima risposta sembra essere la retta, perché lo spazio che deve percorrere l'oggetto risulterà minore che con qualsiasi altra traiettoria, ma bisogna osservare che se la traiettoria è molto inclinata verso il basso l'oggetto acquisterà molta velocità in poco tempo, quindi bisogna trovare il giusto "equilibrio" tra pendenza e brevità del percorso: questo equilibrio si trova appunto nella cicloide.

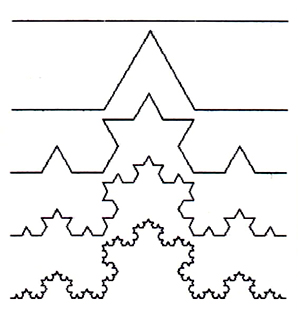
CURVA DI KOCH

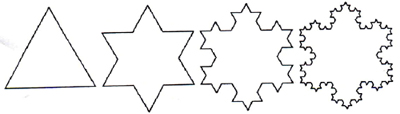
Nel 1904, il matematico svedese Helge van Koch creò una curva che cambiava così tante volte direzione che un viaggiatore che si fosse improvvisamente trovato in un suo punto non avrebbe saputo in quale direzione muoversi. La curva di Koch, o a fiocco di neve , inizia come perimetro di un triangolo equilatero. Inserendo al centro di ciascun lato un nuovo triangolo equilatero di lato pari ad 1/3 del lato di quello precedente, la figura diventa così una stella a sei punte. Il perimetro della stella è costituito da 12 segmenti e ha una lunghezza pari a 4/3 rispetto a quella del triangolo di partenza. Il passo successivo consiste nell'aggiungere altri 12 triangoli più piccoli nel centro del lato di ogni stella. Continuando il processo mediante l'inserimento di triangoli sempre più piccoli, si ottiene il fiocco di neve di Koch. Tra due punti qualsiasi della curva c'è un numero infinito di zig-zag ed è inoltre infinita la distanza tra due suoi punti qualsiasi, anche se la curva circoscrive un'area finita non molto più grande di quella del triangolo di partenza. Si suppone che, al primo stadio della sua costruzione, la curva a fiocco di neve abbia lato 1 centimetro. Con una risoluzione di 1 centimetro, la curva appare come un triangolo composto da 3 segmenti di retta; le pieghe più piccole non sono visibili. Se la risoluzione passa ad 1/3 di centimetro, i segmenti sono 12, ciascuno lungo 1/3 di centimetro. Ogni volta che l'unità di misura viene ridotta a 1/3, il numero di segmenti visibili aumenta di 4 volte. Un comportamento così strano ha portato i matematici di inizio Novecento a definire questa ed altre curve come mostruosità matematiche .

CLOTOIDE

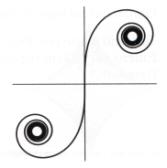
Cloto era quella delle tre Parche che filava lo stame della vita, avvolgendolo sul fuso: per questo poetico riferimento alla curva con il suo doppio andamento a spirale, che ricorda l'avvolgimento attorno alla rocca e al fuso, fu dato dall'italiano E.Cesàro agli inizi del '900 il nome della Parca.

Tale curva fu però inizialmente studiata da Eulero nel 1700 in risposta a un problema posto da Giacomo Bernoulli.

In seguito fu utilizzata nel 1800 da Marie-Alfred Cornu, professore di fisica all'Ecole Politechnique di Parigi, nelle sue ricerche sulla diffrazione.

Alla fine degli anni '70 si scoprì che la clotoide era l'ideale per rovesciare verticalmente le persone, mentre prima si era sempre ritenuto logico pensare, per tale scopo, ad una circonferenza. Peraltro, nelle configurazioni circolari degli otto volanti, all'inizio il carrello sale rapidamente, generando una forza centrifuga eccessiva per i suoi passeggeri; al contrario, quando il carrello sta per raggiungere il punto più alto della circonferenza, la sua accelerazione diminuisce in modo tale da far correre il rischio ai suoi occupanti di cadere a testa in giù.

  Per fortuna ecco .......la clotoide che con la sua forma consente un'accelerazione tale da portare sani e salvi gli occupanti nuovamente con i piedi a terra.

Il principio su cui si basa la sorprendente curva è il raggio variabile del suo anello.
Si comprende facilmente tale principio pensando alla rotazione di un peso legato ad una cordicella:esso ruoterà più lentamente se la corda si allunga, più velocemente se la si accorcia (la potenza descrittiva del principio di conservazione del momento angolare!!!).

L'arco di clotoide, con la sua curvatura variabile, in ogni punto direttamente proporzionale alla lunghezza dell'arco stesso (calcolata dall'origine), costituisce il raccordo più razionale tra un rettifilo e una curva circolare e come tale viene utilizzato nelle costruzioni stradali e ferroviarie: la forza centrifuga varia infatti linearmente nel tempo, a velocità costante, dal valore zero (in rettifilo), a valore massimo (in curva) e viceversa.

CONCOIDE

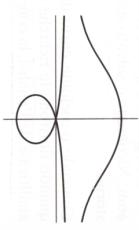
Concoide, curva dalla forma di conchiglia.

Proclo (410-485 d.C.), matematico e filosofo, vissuto ad Alessandria scrisse: " Nicomede risolse il problema della trisezione dell'angolo rettilineo mediante le curve concoidi, delle quali scoprì le proprietà, e determinò la generazione, l'ufficio e le qualità caratteristiche ".

Nel 1600 quando fiorirono le ricerche sui nuovi metodi della geometria analitica e dell'analisi, la concoide fu una curva assai popolare, tanto che Newton suggerì di considerarla come una specie di curva "di servizio".

Tra le sue applicazioni citiamo, in architettura, il disegno dei fusti delle colonne

Se s è una curva qualsiasi, e A è un punto fisso, su una retta da A, che interseca s in Q, si determinano due punti P e P' tali che QP=P'Q=k (costante). 
Il luogo dei punti P e P' si dice concoide della curva s rispetto al polo A.

Come vedete si tratta di una vasta categoria di curve, e si possono creare a piacimento concoidi relative a curve base differenti, con risultati interessanti.

La concoide del cerchio, rispetto ad un punto sulla sua circonferenza, è la lumaca di E.Pascal. 
Se la costante è uguale al diametro del cerchio, la concoide diventa una cardioide.

La concoide di Nicomede ha come curva di riferimento una retta, con il punto fisso sulla retta;nella curva rappresentata in figura il valore della costante k è maggiore della distanza del punto fisso dalla retta.

L'equazione della curva in coordinate polari è:

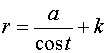
L'equazione parametrica è:

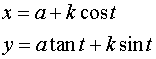
L'equazione cartesiana è:

LITUO

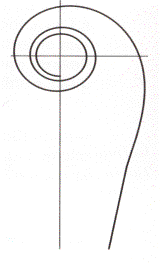
" Baculum sine nodo aduncum, quem lituum appellarunt "
Un bastone ricurvo senza nodi, che chiamarono lituo: 
così Tito Livio descrive il lituus, bastone portato in processione dalla tipica forma a manico ricurvo.

Anche il pastorale dei vescovi e degli abati, impugnato con la sinistra e con la parte aperta del manico rivolta verso i fedeli, ha la stessa forma.

Alla curva matematica, rappresentata in figura, fu così dato
il nome di lituo dal matematico Maclaurin nel 1722 nella
sua opera Harmonia Mensurarum.  

Evidentemente i matematici del XVIII secolo avevano una bella cultura classica.

Essa è simile anche alla voluta di un capitello ionico.

Il gesuita Gerolamo Saccheri (1667-1733), geniale matematico, la chiamò tromba e in effetti Orazio e Virgilio indicano con il nome lituus una tromba di ottone ricurva verso il fondo.

Il lituo ha come equazioni in coordinate polari:

ed è quindi un caso particolare della famiglia di spirali di equazione:

CATENARIA

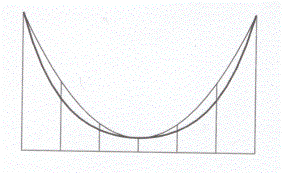
Ne La vita del ragno J.H.Fabre, attento ed acuto osservatore della natura in tutte le sue espressioni, dice: "in una ragnatela, a causa della loro igroscopia, i fili (con la rugiada del mattino), sono carichi di goccioline, e piegandosi sotto il peso, sono divenute altrettante catenarie".

  Nella figura viene mostrata la curva catenaria, descritta da una catena appesa, sovrapposta alla parabola risultante quando alla catena si appendono dei tiranti, che sorreggono un ponte sospeso.

Galileo che era riuscito a dimostrare che la traiettoria di un proiettile, in assenza di resistenza dell'aria, è una parabola, studiando la curva di sospensione di una catenella flessibile o di una fune, credette di avere scoperto un'altra applicazione della parabola, ma era in errore. Un matematico tedesco, Jungius, dimostrò nel 1669 che la curva non era una parabola.

Fu, poi, Huygens, insieme a Leibniz e Jean Bernoulli, che in risposta ad una sfida posta da Jacques Bernoulli, dimostrò nel 1690-91 che tale curva, battezzata da Huygens catenaria, era una curva non algebrica.

Vicino al vertice la catenaria e la parabola sono quasi coincidenti, ed è quindi comprensibile l'errore di Galileo.

Le due curve sono diverse se sono costituite da materiale pesante: nella catenaria la distribuzione del peso della catena è uniforme per ogni lunghezza di arco; nei ponti sospesi invece, dove alla catena sono appesi i tiranti che sostengono il piano del ponte, la distribuzione del peso è uniforme per unità orizzontale di lunghezza e la curva descritta è una parabola.

Nella catenaria agiscono soltanto sforzi di trazioni; non sono presenti sforzi di flessione.

Proviamo ora a rovesciare una catenaria.

La curva così ottenuta viene usata molto in architettura. Infatti, in una catenaria rovesciata  compaiono soltanto sforzi di compressione; perciò essa rappresenta la forma migliore che può assumere un arco per sostenere il proprio peso, così come la parabola rappresenta la forma migliore che può assumere un arco per sostenere un carico uniforme.

Dopo la scoperta della catenaria e delle sue proprietà, nel XVIII secolo fiorirono molti studi per le sue applicazioni pratiche: ad esempio Christopher Wren  usò una struttura a catenaria per la costruzione della cupola di St Paul a Londra. 

Curiosità: se facciamo rotolare una parabola lungo una retta il fuoco della parabola descrive una catenaria.

I PONTI SOSPESI

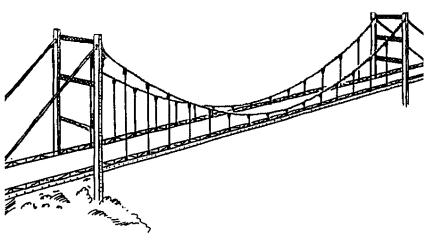
La costruzione di un ponte, problema che per la sua utilità ha suscitato interesse fin dall'antichità, richiede, in alcuni casi, l'impiego di un'elevata tecnologia e spesso la soluzione trovata è stata perfezionata solo in tempi successivi. Fra i ponti con luci libere più grandi, i più imponenti sono sicuramente i ponti sospesi, ponti cioè in cui l'impalcato è sospeso mediante tiranti in acciaio ai cavi portanti disposti secondo una certa curva e sostenuti da alti piloni.

Il Golden Gate, sulla baia di S. Francisco, è uno dei ponti maggiori di questo tipo; è stato costruito negli anni '30. Quello che forse non tutti immaginano è che i cavi d'acciaio del Golden Gate hanno 93 cm di diametro e sono formati da 27500 "fili" di 6 mm di diametro, pesano da soli circa 15.000 tonnellate e sostengono un impalcato a 75 m dal mare. Le torri sono alte 223 m sopra il pelo dell'acqua. Questi dati possono forse aiutare a capire l'interesse non solamente matematico per calcolare la "certa curva" lungo cui si dispongono i cavi in modo da conoscere la lunghezza dei tiranti prima di aver iniziato la costruzione del ponte.

La curva che si ottiene fissando per i due estremi una fune senza alcun peso si chiama appunto catenaria e a prima vista potrebbe sembrare la curva lungo cui si dispongono i cavi del nostro ponte. In realtà tenendo conto delle forze che agiscono sui cavi a causa del peso dell'impalcato questi si dispongono lungo curve paraboliche. Nei grandi ponti sospesi, dove il peso delle catene è dello stesso ordine di grandezza del piano stradale, la curva risultante è a metà tra la parabola e la catenaria

CARDIOIDE

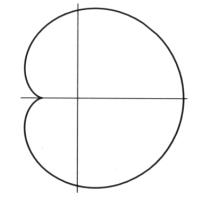
La cardioide, un nome usato per la prima volta da Castillon  in un articolo su Philosophical Transactions of the Royal Society del 1741.

La sua lunghezza e' stata trovata da La Hire nel  1708, ed egli perciò ha un certo diritto ad essere nominato come lo scopritore della curva. E' un caso speciale della lumaca Pascal  e perciò, in un certo senso, il suo studio va indietro nel tempo molto prima di Castillon o La Hire.

L'equazione polare della cardioide è: