Indagine statistica

La questione sociale

Economy of Communion

ISTITUTO STATALE DI ISTRUZIONE SECONDARIA SUPERIORE

Istituto Tecnico Commerciale e per Geometri

“Francesco Daverio” - Varese

Indagine statistica

Le reti di computer

5 per mille e non profit

Homepage

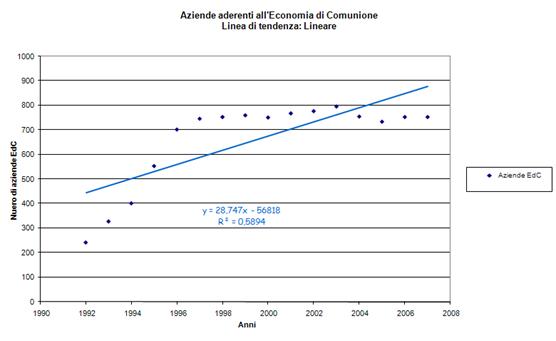
Partendo dai dati (tabella 1), rappresentanti il numero di aziende che negli anni hanno aderito al progetto di Economia di Comunione, si vuole cercare la funzione che li rappresenta. Per la difficoltà di calcolo che questa operazione comporta, ci si “accontenta” di una funzione elementare, più semplice, che - graficamente - si accosta, con una minima tolleranza, alla funzione ricercata.

Il metodo dei minimi quadrati consente di trovare la funzione, stabilito il modello di partenza, che rende minima la somma dei quadrati delle differenze tra valori teorici e osservati.

Iniziamo con la più semplice: la retta.

Per trovare i coefficienti a e b che rendono minima la funzione S(a,b) bisogna calcolare le derivate prime parziali S'_a e S'_b, porle uguali a zero e risolvere il sistema.

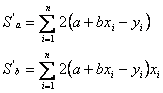
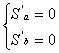
Quindi si può risolvere il sistema nel caso specifico, sostituendo i dati raccolti nella tabella alle x e y, oppure risolverlo tramite il calcolo letterale per ottenere le formule che permettono, in situazioni simili, di ricavare i valori a e b dell’equazione della retta senza dover reimpostare tutto dall’inizio.

 

Se si moltiplicano le due equazioni del sistema, rispettivamente per ∑x_i e n

e si risolve il sistema per differenza, si ottiene un’equazione nella sola incognita b.

 

Quindi

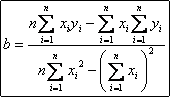
a, invece, si può ricavare semplicemente dalla prima equazione del sistema

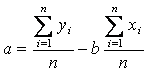
Quindi

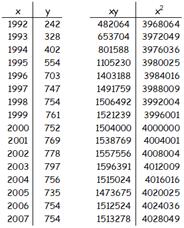
Applicando le formule trovate (tabella 2):

Per verificare la bontà della funzione ricavata, si calcola un indice: l’indice di determinazione (R²) che assume valori compresi tra 0 e 1. R² è uguale a 1 quando tutti i punti appartengono alla funzione (nel caso della retta, quindi, sono tutti allineati). Perciò più il valore di questo indice è prossimo a 1, più la funzione trovata si accosta a quella reale.

Valori accettabili di questo indice sono maggiori a 0,85.

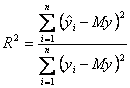
In questo caso, R² = 0,5894. Perciò la retta non è un modello adatto a rappresentare la funzione.

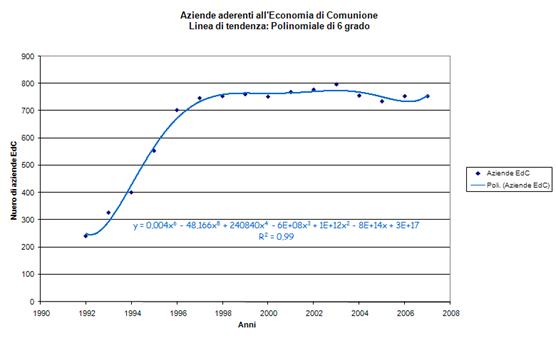
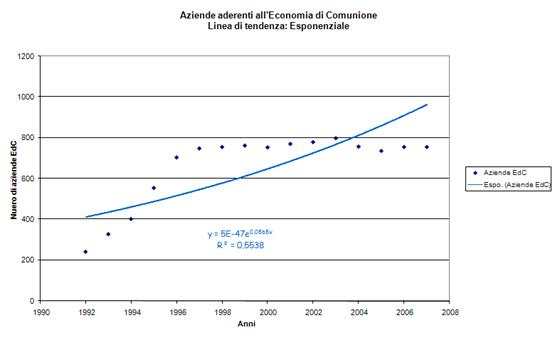
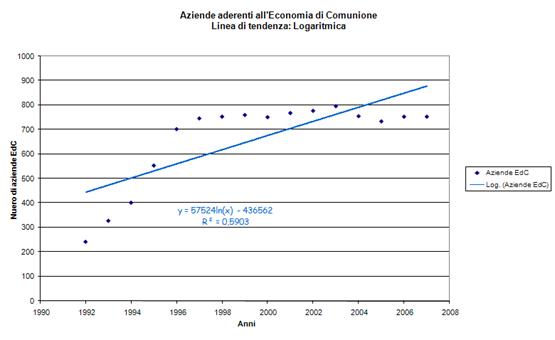
I fogli elettronici sono strumenti adatti a questo tipo di studio. In seguito riporto alcuni grafici a dispersione costruiti con MS Office Excel, contenenti linee di tendenza di diverso tipo, le corrispondenti equazioni e indici di determinazione. (click per ingrandire)

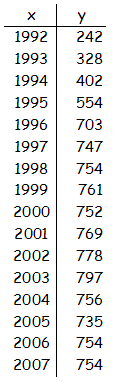
tabella 1

tabella 2