Quando si parla di magnetoterapia il flusso magnetico viene espresso in Gauss e siccome questo viene generato da una bobina opportunamente alimentata, si può trovare il legame tra il numero di spire il raggio delle spire e la corrente che circola nelle spire e i Gauss generati.

L'induzione magnetica viene definita come il prodotto del coefficiente µo per l'intensità del campo magnetico H e si misura in Tesla cioè:

Dove per una spira

H vale:

pertanto l'induzione magnetica B diventa:

per più spire si avrà:

sapendo che 1 Tesla = 10^4 Gauss, l'induzione B in gauss sarà:

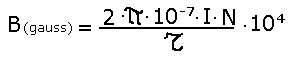
se il raggio lo esprimo in millimetri al posto di metri e semplifico si ottiene:

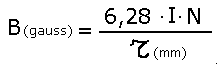
Si deduce che i Gauss aumentano all'aumentare all'Intensità di corrente in Ampere e al numero di spire della bobina oppure diminuendo il raggio medio dell'avvolgimento.

Esempio: supponiamo di voler ottenere 100 gauss da una bobina.

Fisso il raggio medio di 50 mm e determino il prodotto I x N

I N = 100 x 50/6,28 = 796 scegliendo una corrente non eccessivamente alta ad esempio 0,5A avremo che N = 796/0,5 = 1592 Spire.

Troviamo ora la lunghezza del filo per poter risalire al suo diametro e alla sua resistenza così da poter determinare il voltaggio da applicare per poter far scorrere 0,5A previsti.

Circonferenza = 6,28 x raggio medio = 50 x 6,28 = 314 mm che moltiplicato per il numero delle spire avremo cke la lunghezza in metri

L = 0,314 m x 1592 = 500 metri

Osservando la tabella seguente

trovo che il filo di rame smaltato in grado di portare 0,5 A é quello con il diametro di 0,405 mm il quale offre 0,149973 Ohm al metro.

Le 1592 spire (a forma di mazzetto) occuperanno un'area di 1592/609 = 2,6 cm² ne consegue che il raggio interno della bobina sarà di 82 mm e quello esterno sarà di 118 mm.

La resistenza di 500 m di questo filo sarà 500 x 0,149973 = 75 Ohm

La bobina peserà 500 x 1,09984 = 550 grammi

Conoscendo ora la sua resistenza e dovendo passare 0,5 ampere avremo che la tensione da applicare alla bobina affinché passi la corrente voluta

sarà V= R x I = 75 x 0,5 = 37,5 V

Altro esempio

Ho avvolto una bobina su un supporto del diametro di 6 cm con filo
(nudo Ø 0,40 mm) smaltato del diametro di 0,425 mm.

L'area occupata dal mazzetto é di 18 x 12 mm = 2,16 cm²
Dalla tabella trovo che le spire avvolgibili al cm² sono 553 il che comporterebbe un numero di spire N = 553 x 2,16 = 1194
Ma allo stesso risultato ci dovrei arrivare misurando la resistenza del filo che é risultata 26 Ohm dividendola per gli Ohm al metro e trovare cosi i metri totali che divisi per la circonferenza media mi danno le spire.

L filo = 26 / 0,13535 = 192 m

La circonferenza media é data diametro interno + diametro esterno diviso 2 x 3,14 = [(83 + 60) / 2]* 3,14 = 224,5 mm = 0,2245 m

Nsp = L filo / 0,2245 = 192 / 0,2245 = 855 spire

Come si vede sono minori di quelle precedentemente calcolate ma sono le più reali.
Infatti le 1194 sono teoriche se si avvolgesse le spire perfettamente
affiancate senza accavallamenti. Si può pertanto affermare che avvolgendo manualmente le spire in una data sezione ci stanno meno spire di quelle teoricamente ammesse.
Se prendiamo per veritiere le 855 spire si può introdurre un fattore che possiamo chiamare di stipamento che sarà dato da 1194 / 855 = 1,39.
Pertanto le spire teoriche avvolgibili per cm² segnate sulla tabella per renderle reali per avvolgimenti manuali vanno divisi per 1,39.

Da che corrente dovrà essere percorsa la bobina se dovrà generare un flusso magnetico B di 50 gauss ?

Dalla dimostrazione di inizio pagina sappiamo che

B(gauss) = (6,28 x N I) / Raggio medio   dove Raggio medio = 35,75 mm

B(gauss) = (6,28 * 855 / 37,75) * I = 150 * I

da cui I = B / 150 = 50 / 150 = 0,333 A = 333 mA

A conferma che i conti sono corretti partendo dal peso della bobina che é di 220 grammi si può trovare quanti metri sono dividendo per il peso del rame nudo al metro cioè 220 / 1.119096 = 196 m invece che 192 (se poi si dovesse considerare 5 grammi di vernice per lo smalto e si rifanno i calcoli con 215 g si ottiene perfettamente 192).

Ho misurato l'induttanza con ponte RLC (HP4261A) e ho ottenuto 55 mH
Con il programma BOBINE.EXE (opzione 2) ho voluto verificare quante spire avrei dovuto avvolgere su un supporto da 6 cm con lunghezza dell'avvolgimento di 1,8 cm e filo da 0,425 mm di diametro per ottenere 55 mH (55000 µH) e ho ottenuto 819 spire anziché 855.

VERIFICHE PRATICHE

Dopo aver esaminato il problema delle bobine dal punto di vista teorico e aver verificato la corrispondenza dei parametri fisici di alcuni prototipi realizzati non rimaneva che verificare anche la corrispondenza dei gauss mediante l’utilizzo di una sonda "Hall IC" tipo MLX90215 della Melexis.

Tale sonda è in grado di misurare da –2000 a + 2000 Gauss

É stato realizzato il seguente schema (Sch.1) di collegamento in modo da poter attaccare il multimetro in portata mV così da leggere direttamente i Gauss (1 mV = 1 Gauss). [regolare il trimmer per 000mV a 0 Gauss]

Se la corrente gira in senso sinistrorso nelle spire della bobina appoggiata sopra alla sonda, tenendo lo smusso identificativo della stessa come nello schema, i mV (Gauss) saranno positivi e il NORD del campo magnetico è rivolto verso l’osservatore.

Sistemata la sonda su di un piano d’appoggio al centro delle bobine alimentate in corrente continua il multimetro indicava un quantitativo di Gauss corrispondenti a quelli calcolati con tolleranza accettabile, ± 3 %.

ANDAMENTO DELL’INDUZIONE MAGNETICA

Spostando la sonda sull’asse del piano d’appoggio della bobina dal centro verso la periferia dell’avvolgimento e riportando in una tabella di Excell i Gauss in funzione della distanza si è potuto tracciare il seguente grafico:

Comparando la medesima curva ottenuta per altre bobine con supporto inferiore ho intuito che per appiattire i due picchi, per avere un flusso più uniforme, era necessario avere il raggio medio dell’avvolgimento pari al diametro interno del vuoto.

Pertanto prendendo in esame la formula teorica dove il flusso vale:

B(gauss) = (6,28*N*I) / r m

in cui N = numero delle spire

I = corrente in ampere

r m = raggio medio della bobina in millimetri

si è creato una tabella (Tab. 1) che, fissato il diametro del supporto, lo spessore della bobina, il diametro del filo e la corrente in ampere, mostra l’andamento dei gauss in funzione delle spire.

Tab. 1

diam. filo	0,4	mm smaltato		peso specifico		8,91
spessore	11	mm		ró in funz. della temp.		0,017069
diam. Sup.	29	mm		Ohm al metro		0,136581
Corrente	0,50	Ampere		grammi al metro		1,009984
				Spire x Strato		19,78417
spire	raggio medio mm	metri filo	peso grammi	resistenza Ohm	gauss	potenza watt	diametro ester. mm
950	24,1	143	157	19,5	123	4,9	67
975	24,5	149	164	20,3	125	5,1	68
1000	24,6	154	169	21	127	5,3	69
1025	24,8	160	176	21,8	129	5,5	70
1050	25,1	165	181	22,5	131	5,6	71
1075	25,3	171	188	23,3	133	5,8	72
1100	25,6	176	193	24	134	6	73
1120	25,8	181	199	24,7	136	6,2	74
1145	26,1	187	205	25,5	137	6,4	75
1170	26,3	193	212	26,3	139	6,6	76
1195	26,6	199	219	27,1	141	6,8	77
1220	26,8	205	225	27,9	142	7	78

Fissando inoltre la resistività del filo di rame a 22 ° C pari a 0,017069,

ricavata dalla formula r = 0,0156 *(1 + 0,00428 * ° C), e il peso specifico del rame di 8,91 grammi al metro per mm² nella tabella vengono espressi pure la resistenza del filo, il peso complessivo della bobina in grammi e la lunghezza totale del filo in metri.

Conoscendo lo spessore della bobina e il diametro del filo si calcola il numero di spire per ogni strato

Spire Strato = Spessore Bobina / (f filo *1,39)

dove 1,39 è il fattore di stipamento per bobine avvolte a mano.

Il raggio medio sarà dato da:

r m = ½ f supporto + ½ [(Nr spire tot. /spire-strato) * f filo]

tutto espresso in millimetri

La lunghezza del filo in metri sarà:

lunghezza = (Nr spire tot. * r m * 6,28)/1000

lunghezza in metri r m in millimetri

Il peso della bobina in grammi sarà dato dal peso del filo nudo più il peso della vernice che è circa il 4 %:

peso di 1 m di filo 1 mm² di sez. = 8,91 * p * raggiofilonudo²

raggiofilonudo = (f filo – 0,022)/2

0,022 = spessore vernice

peso bobina = metri filo * 8,91 * p * raggiofilonudo²

La resistenza del filo in Ohm sarà data dal (ró) r (1 metro di filo di 1 mm² di sez.)

R = r * p * raggiofilonudo² * metrifilo

La tensione ai capi della bobina sarà: V = R * I

la potenza dissipata dalla bobina in watt = R*I²

Con tabella più ampia si è tracciato il seguente grafico

Potendo simulare con Excell, cambiando i valori del supporto, spessori della bobina e diametro filo ecc., ed osservando l’andamento dei vari paramenti sul grafico, si è dedotto che il miglior compromesso, tra spire, gauss, peso e resistenza, cercando di ottenere un raggio medio pari circa al diametro interno, si ottiene con bobine aventi un numero di spire compreso tra 950 e 1200 spire.

Pertanto il nuovo grafico si riduce al seguente:

Per una ulteriore riprova a verifica di quanto fino qui sostenuto si è avvolta una ulteriore bobina di 1120 spire come dai dati segnati in rosso nella tabella 1, o indicati in blu nel qui sopra riportato grafico misurando i seguenti valori:

CORRENTE CONTINUA DI ALIMENTAZIONE = 0,5A
GAUSS MISURATI = 126
RESISTENZA FILO = 24,5 Ohm
PESO TOTALE =200 grammi

Rispondenti ampiamente a quelli calcolati e indicati in tabella.

Come si può osservare dal seguente grafico è migliorato anche la distribuzione dei picchi massimi del flusso magnetico.

La massima concentrazione dei Gauss si ha sulla linea della circonferenza interna dell’avvolgimento, mentre su quella esterna si ha un massimo di polarità opposta molto meno accentuato.

Il flusso magnetico si annulla e va a zero Gauss a pochi millimetri dalla fine dell’avvolgimento per poi risalire, come già detto, con polarità invertita. Con nucleo ferro-dolce a parità di corrente i Gauss circa raddoppiano.

CONSIDERAZIONI CONCLUSIVE

Per avere effetti biologici significativi, le bobine vanno alimentate con correnti continue impulsive con duty-cycle variabile tra il 10 e 40% (pare si possa restringere tra 20 e 30%) e con frequenze comprese tra 1 e 100 Hz.

Quanto sopra esposto equivale, in termini di tempo, ad alimentare e di conseguenza generare impulsi magnetici di una certa intensità, per tempi compresi tra 1mS e 400mS.

Un mS si avrà per duty-cycle al 10% e frequenza 100 Hz mentre 400 mS si avrà per duty-cycle al 40% e frequenza 1 Hz.

Duty-cycle al 10% è da intendere che, fatto 100 il tempo che intercorre tra un impulso e l’altro, la durata del tempo in cui c’è induzione magnetica vale 10 mentre il tempo in cui non c’è induzione magnetica vale 90.

L’induzione magnetica media misurata in Gauss a fini terapeutici può variare tra decine di Gauss fino ad un massimo di circa 100 Gauss.

Si parla di valori medi in Gauss in quanto la bobina è appunto alimentata ad impulsi. Per avere ad esempio mediamente una induzione magnetica di 100 Gauss con duty-cycle del 40% si dovranno utilizzare bobine capaci di generare un flusso impulsivo di 250 Gauss oppure capaci di generare un flusso di bene 1000 Gauss per duty-cycle del 10% (è bene non andare oltre i 1000 Gauss pari a 0,1 Tesla se non per casi diagnostici particolari).

A tal proposito si ricorda che le raccomandazioni in vigore negli USA, inerenti le esposizioni a campi magnetici omogenei per lunghi periodi, limitano a 200 Gauss l’intensità massima sicura.

Per ottenere molti Gauss servirebbero bobine con molte spire, dal diametro piccolo o molta corrente.

Ma molte spire significa aumentare la resistenza del filo che, per la legge di Ohm, non permette di salire con la corrente se non aumentando la tensione a valori proibitivi anche dal punto di vista della sicurezza con dissipazione di potenza esagerata che surriscalderebbe la bobina stessa.

Come già precedentemente accennato, un buon compromesso si ottiene con bobine di dimensioni tra i 60 e 80 mm di diametro composte da un migliaio di spire avvolte su supporto del diametro di 20/30 mm con filo di rame smaltato del diametro di circa 0,4 / 0,42 mm percorse da correnti massime di poco più di 1A per raggiungere induzioni magnetiche massime tra i 250 e 300 Gauss.

Si possono pertanto mantenere alimentazioni con tensioni attorno ai 20 / 30 Volt dissipando potenze (in calore) inferiori ai 10W.

Table A, Comparazione fra unità di misura magnetiche

Unità	Simbolo	Sistema cgs	Sistema SI	Sistema English
Flusso	f	Maxwell	weber	Maxwell
Densità di flusso	B	Gauss	Tesla	linea/in²
Forza di magnetizzazione	H	Oersted	ampere spire/m	ampere spire/in

Table B, Conversione fra unità di misura magnetiche

Moltiplica	per	e ottieni
Linea/cm²	1	Gauss
Linea/cm²	1	Maxwell/cm²
Linea/in²	0.155	Gauss
Linea/in²	1.55 x 10 -5	Tesla
Gauss	6.45	Linea/in²
Gauss	10 -4	Tesla
Oersteds	79.577	Ampere spire/m
Ampere spire/in	0.495	Oersteds
Ampere spire/in	39.37	ampere spire/m

Inch = in = 0,0254 metri

Sito correlato       Circuito per la magnetoterapia

INDEX             Torna indietro