Grafica della tartaruga



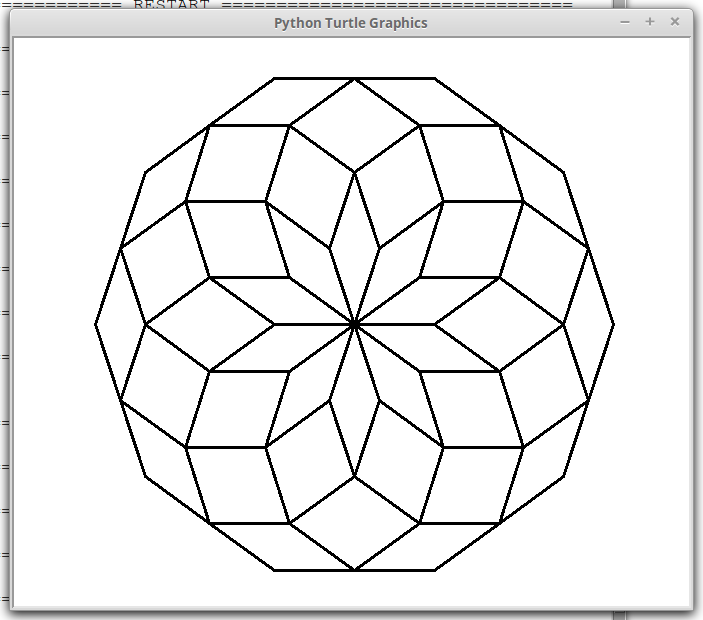
Procedura poli



def poli(lato, angolo):
    turtle.forward(lato)
    turtle.right(angolo)
    somma = angolo
    while somma % 360 != 0: #mentre somma modulo 360 è diverso da zero 
        turtle.forward(lato) #cioè il resto nella divisione intera per 360 è diverso da 0
        turtle.right(angolo)
        somma = somma+angolo

Questa procedura disegna tutti i poligoni regolari al variare del valore dato ad angolo.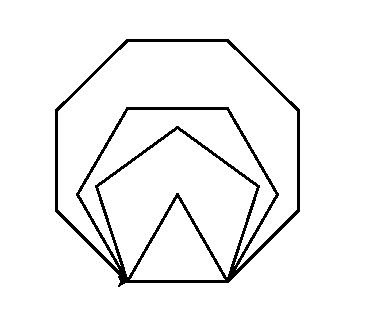



Può disegnare pure poligoni "intrecciati" con lati uguali e angoli esterni uguali.


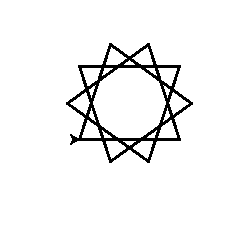
Poli con angolo 108


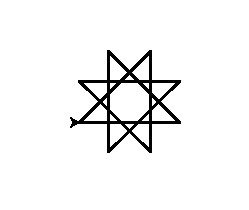
Poli con angolo 135


Poli con angolo 144

In sostanza nella procedura poli si ripete avanti(lato) e destra(angolo) finchè la
rotazione totale della tartaruga contenuta in somma diventi un multipli di 360°.

Questo si verificherà quando la divisione intera per 360 è zero.


Poli(1,1)



Le implicazioni matematiche e informatiche di questa semplice procedura sono state indagate
a fondo da Harold Abelson e da Andrea DiSessa nel loro splendido libro "La Geometria della Tartaruga" Muzzio Editore.

Numero di lati e rotazione nella procedura poli


Il cammino percorso dalla tartaruga con la procedura poli è un cammino chiuso:
la tartaruga ritorna nella posizione iniziale e nella orientazione iniziale.
Il numero n dei lati di un poligono disegnato con la procedura poli, si ottiene dividendo
il minimo comune multiplo fra 360 e l'angolo assegnato in input alla procedura, per l'angolo
stesso:

n= mcm(360, angolo)/angolo

Il numero di angoli giri di cui ruota la tartaruga si ottiene così:

R=mcm(360, angolo)/360

Vediamo un esempio:


Il poligono di 24 lati intrecciati con angolo 75° si ottiene dopo una rotazione totale di
1800°. Ora il mcm fra 360 e 75 è dato da 1800 e dividendo 1800 diviso 75 si ottiene il numero
n=24 dei lati. Inoltre dividendo 1800 diviso 360 si ottiene il "numero di rotazione" del percorso
della tartaruga che in questo caso è 5.

Algoritmo di Euclide

Per trovare il mcm partiamo dal Massimo Comun Divisore con l'algoritmo di Euclide:

def euclide(a,b):
    if a==b:
        return a
    if a>b:
        return euclide(a-b,b)
    if a


Questo algoritmo si può rendere più veloce:



    
def euclide_veloce(a,b):
    if a % b ==0:
        return b
    else:
        c = a % b
        return euclide_veloce(b, c)




Nel Python il simbolo % indica il resto nella divisione intera e == opera un confronto.

Volendo trovare il minimo comune multiplo, utilizziamo la proprietà per cui il prodotto 

di due numeri è uguale al prodotto di mcm e MCD:



def mcm(a,b):
    return a*b/euclide_veloce(a,b)




Dimostrazione.









 
 
 
 
 
 
 


 

Tutti i poligoni creati con la procedura POLI sono inscritti in un cerchio
 


 Per dimostrare che tutti i poligoni creati da poli hanno i vertici su di una circonferenza

 partiamo dalla seguente figura:


 

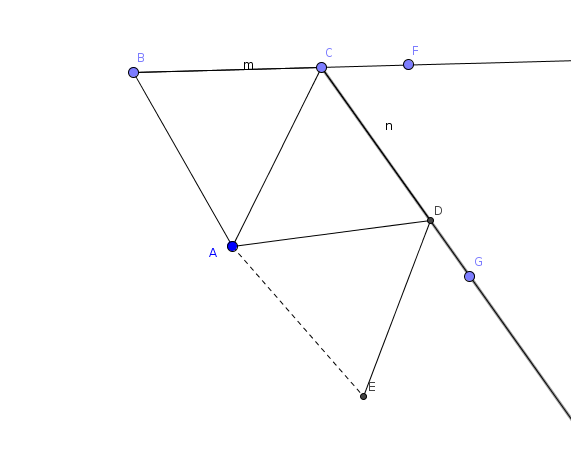
 In figura BC, CD e DE sono tre lati consecutivi uguali ottenuti da poli con la ripetizione di avanti(lato).

 destra(angolo) esterno.

 Per i punti non allineati B, C, D passerà una circonferenza di centro A. Raggi di questa sono

AB, AC, AD. Bisogna dimostrare che E appartiene alla circonferenza e cioè che AE è un raggio.


Sappiamo che i due angoli esterni FCD e GDE sono uguali.

Saranno uguali gli angoli supplementari BCD e CDE.

Sottraendo da questi due, angoli uguali, otterremo angoli uguali.

Sottraiamo gli angoli BCA e CDA. Rimane che l'angolo ADE è uguale a BCA.

I seguenti angoli sono uguali: BCA, ACD, CDA, perchè AB, AC e AD sono raggi della stessa circonferenza

Abbiamo dimostrato che anche l'angolo ADE è uguale ai tre angoli.

Ma allora anche i triangoli ACD e ADE sono uguali dato che hanno CD = DE (due lati), AD in comune

E gli angoli compresi CDA e ADE uguali. Quindi AD = AE.













  
 
 
 

Cerchio circoscritto ad un poligono 









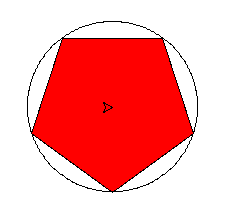
Tutti i poligoni creati con la procedura POLI sono inscritti in un cerchio.

Si vuole mostrare come disegnare il cerchio circoscritto con la grafica della tartaruga.








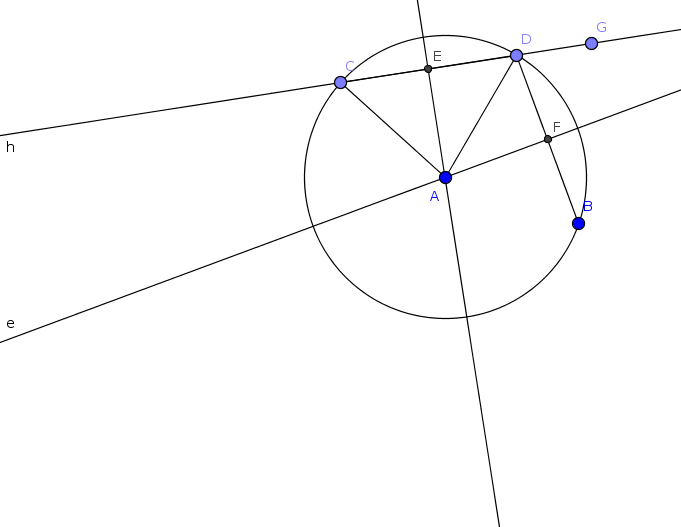
Nel grafico CD e DB sono due lati consecutivi uguali disegnati da POLI. L'angolo esterno di cui ruota la tartaruga è GDB. Gli assi dei due segmenti CD e DB si incontrano nel centro del cerchio circoscritto A.


L'angolo EDA è dato da (180-angolo)/2. Dove angolo è il parametro dato in input alla procedura POLI. L'altro parametro di POLI è la lunghezza del lato che corrisponde a CD. 


Ciò posto con semplici formule trigonometriche si trova AC raggio del cerchio ed EA apotema del poligono inscritto.


Trovato il raggio e l'apotema è necessaria una procedura per disegnare una circonferenza che 

abbia il centro nella posizione corrente della tartaruga con il raggio fornito in input.





Non rimane altro che portare la tartaruga nel centro del poligono regolare e disegnare

la circonferenza circoscritta.


Per fare questo basta fare andare avanti la tartaruga, dalla posizione iniziale, di una distanza pari a lato/2.0 (nel grafico di sopra segmento CE). Far girare quindi a destra la tartaruga di 90 gradi
 
e procedere avanti di una distanza pari all'apotema (segmento EA).


Nella grafica della tartaruga si deve porre attenzione allo stato in cui si lascia la tartaruga

stessa: come una procedura incide su posizione e orientamento di essa.

Se ad esempio si esegue una rotazione a destra di 90°, sarà necessario eseguire una rotazione

a sinistra di 90° per lasciare inalterata l'orientazione iniziale della tartaruga.















La procedura nuovopoli






def poli(lato,angolo):
    fd(lato) #avanti(lato)
    right(angolo) #destra(angolo)
    fd(lato)
    rt(2*angolo)
    somma=3*angolo #somma serve per sommare gli angoli di cui ruota la tartaruga
    while somma % 360 != 0: # mentre il resto della divisione per 360 si mantiene
        fd(lato)            # diverso da 0 esegui avanti(lato) e le altre due
        right(angolo) # istruzioni. Se somma arriva al valore 360 o
        fd(lato)
        rt(2*angolo)
        somma=somma+3*angolo  # multipli di 360 il resto della disione per 360

                            # diventa 0 e il ciclo si ferma




Ecco alcuni risultati:




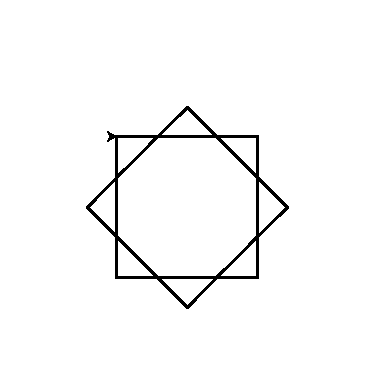
Nuovopoli con angolo 45




Nuovopoli con angolo 60




Nuovopoli con angolo 108




Nuovopoli con angolo 125




Nuovopoli con angolo 135




Nuovopoli con angolo 144









Spirali equiangole







def spi(lato, angolo, passo):
    for i in range(300):
        t.fd(lato)
        t.rt(angolo)
        lato=lato+passo





Ecco degli esempi:




Spirale con angolo 70




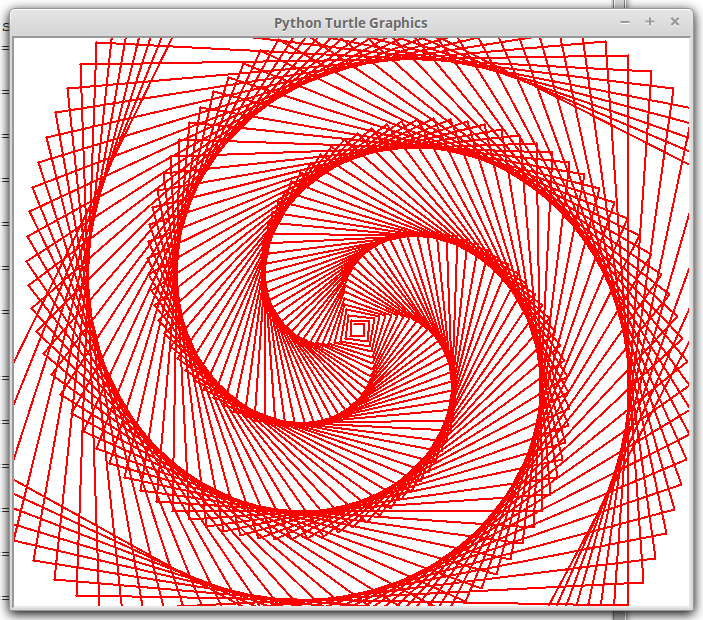
Spirale con angolo 91




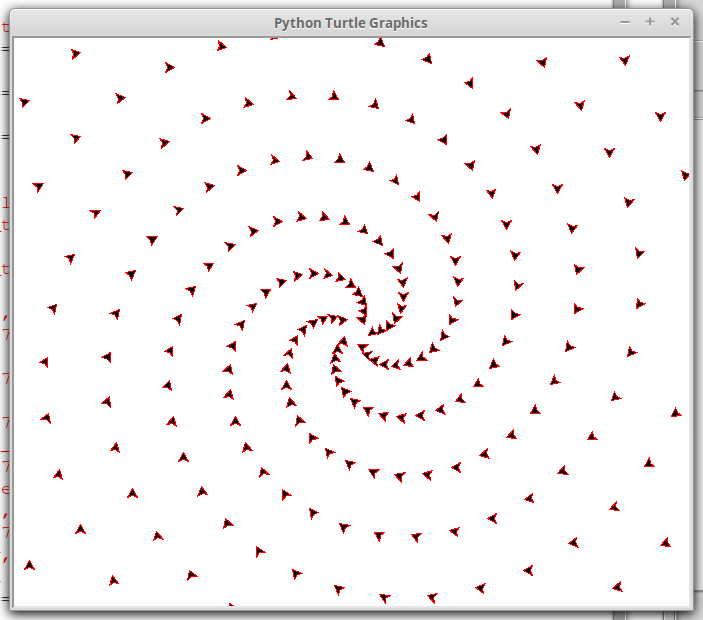
Stampando i vertici con stamp()






Procedura poliruota




def poliruota(lato, angolo):
    for i in range(10):
        poli(lato,angolo)
        turtle.rt(36)



La procedura ripete dieci volte poli partendo da una orientazione diversa.




poliruota angolo 36




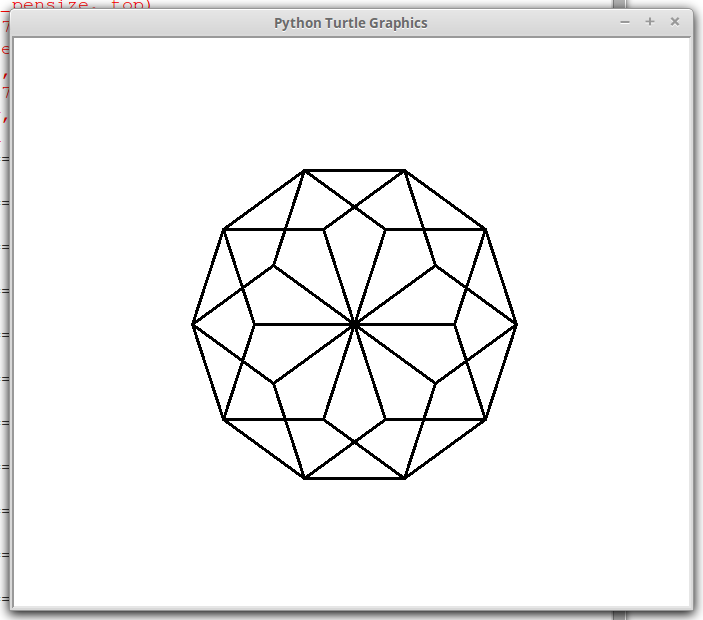
poliruota angolo 72




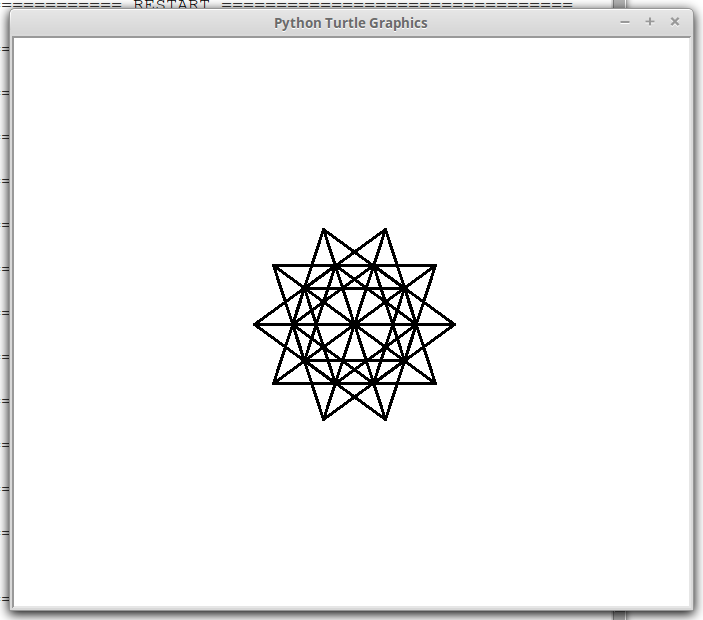
poliruota angolo 144






Quadrati e triangoli ricorsivi




def tri(lato):
    if lato > 4:
        for i in range(3):
            forward(lato)
            right(120)
            tri(lato/2)

def quaric(lato):
	if lato > 4:
		for n in range(4):
			fin.fd(lato)
			quaric(lato/2)
			fin.rt(90)

















Archi











Listato in Python.








Procedura duopoli




def duopoli(lato1, angolo1, lato2, angolo2):
    for i in range(1,200):
        vettore(i*angolo1,lato1)
        vettore(i*angolo2,lato2)

def vettore(direz,lung):
    setheading(direz)
    fd(lung)




Ecco alcuni risultati:




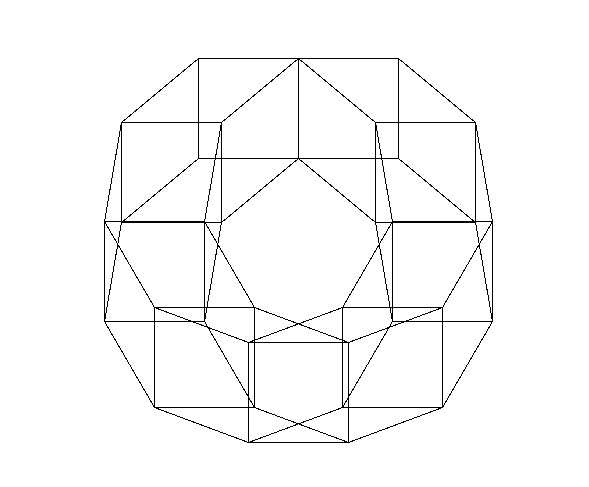
Duopoli con angoli 90 e 320

Un multiplo di 360, si raggiunge ripetendo 4 volte 90. Nel caso dell'angolo 320, bisognerà

ripetere 9 volte la rotazione di 320 per ottenere 2880 = 8 x 360. 

Il cammino si chiude in mcm(4, 9)= 36 passaggi.




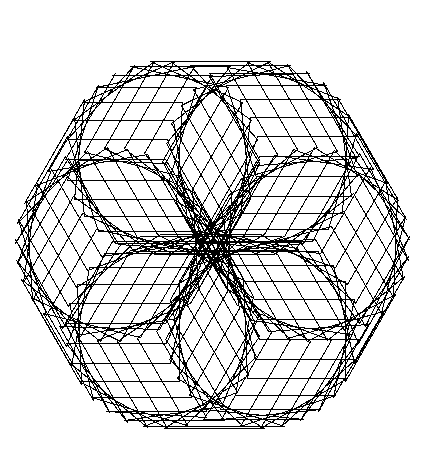
Duopoli con angoli 62 e 300






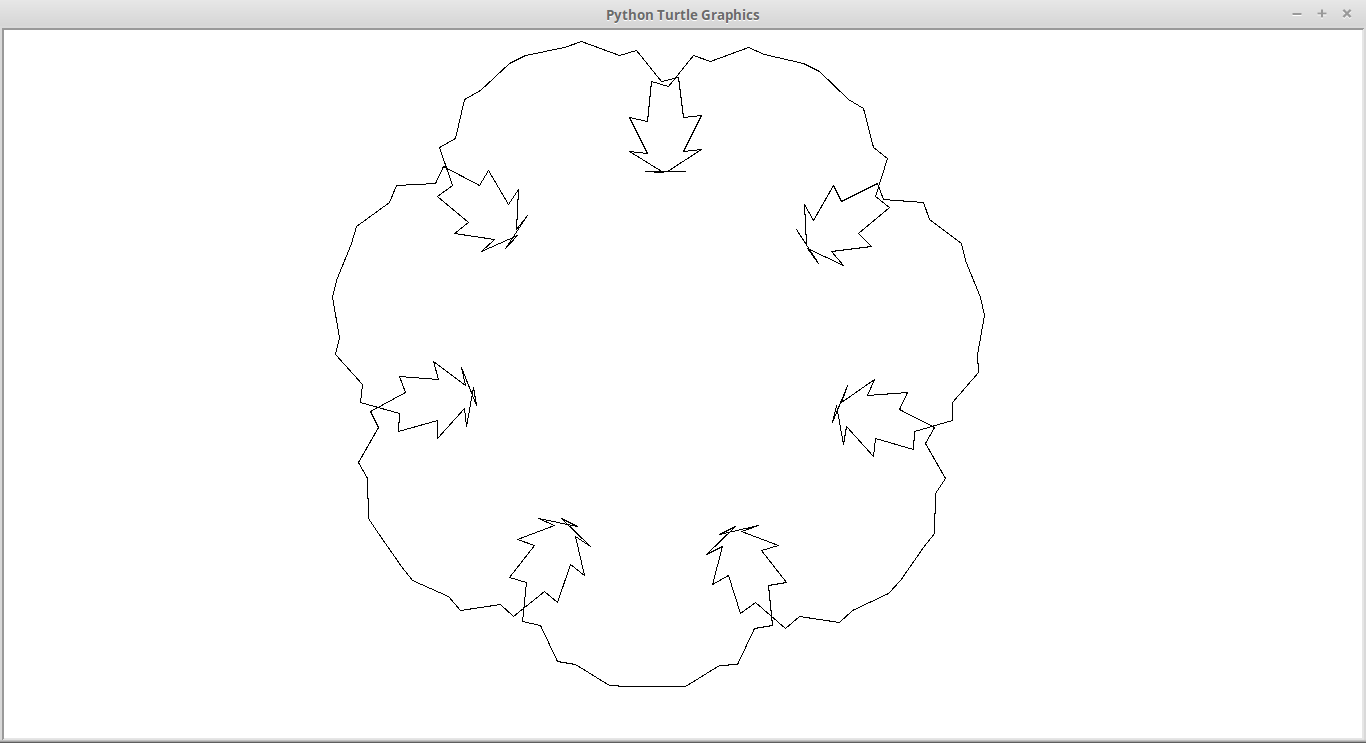
Duopoli con angoli 32 e 4






Duopoli con angoli 19 e -21








Procedura poliforbice



def forbice(dist, fase):
    rt(fase)
    fd(dist)
    left(2*fase)
    fd(dist)
    rt(fase)

def poliforbice(d,A,fase):
    rotaz=0
    for i in range(200):
        forbice(d, fase)
        left(A)
        rotaz=rotaz+A
        #print rotaz
        if rotaz % 360 == 0:
            break








poliforbice con angoli 33 e 66





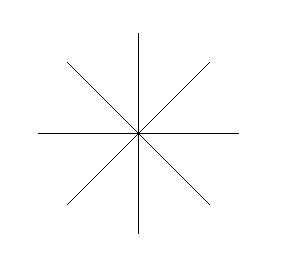
poliforbice con angoli 45 e 90




poliforbice con angoli 90 e 60




poliforbice con angoli 72 e 60




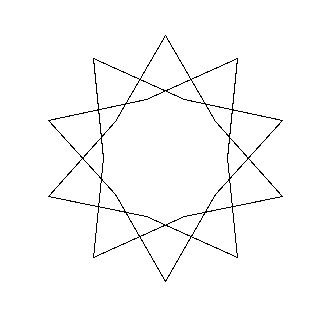
poliforbice con angoli 108 e 60