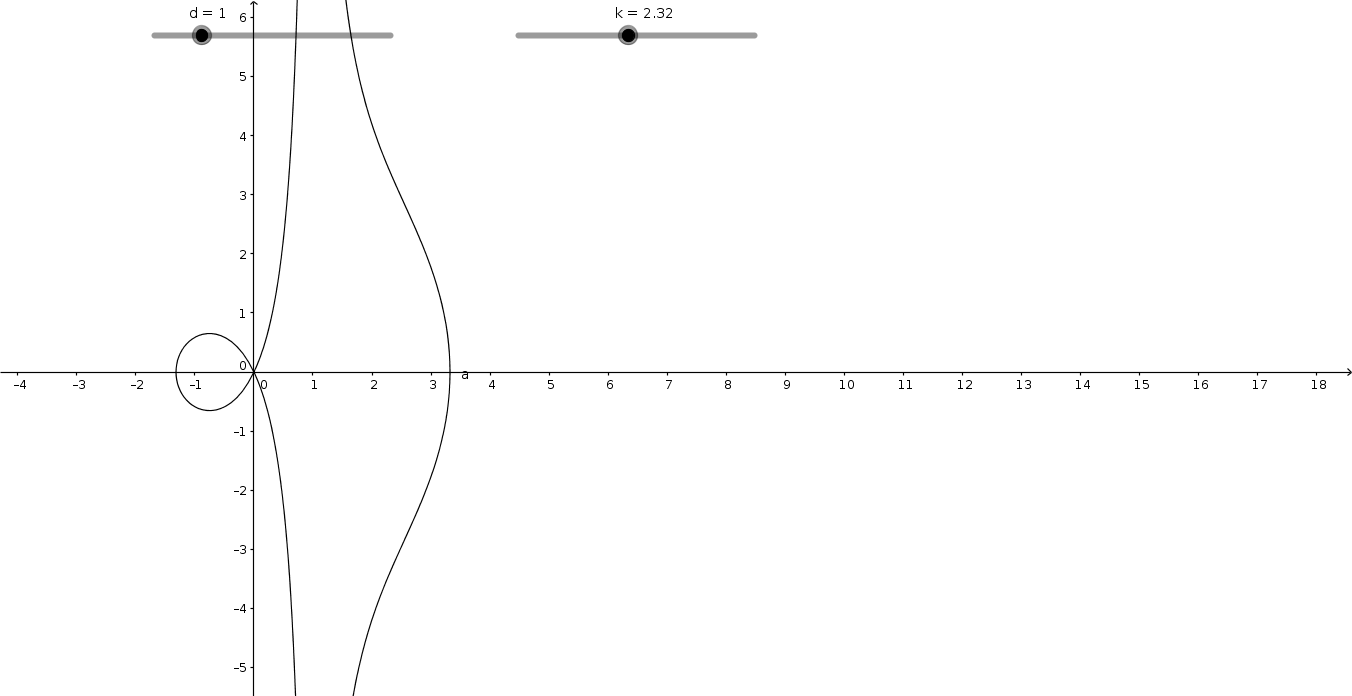
Fu chiamata così perchè ricorda una conchiglia. Di seguito alcune indicazioni per eseguire la sua
costruzione con GeoGebra e per il suo utilizzo nella trisezione di un angolo acuto (divisione di un angolo
in tre parti uguali).

Dato un punto O nell'origine e una retta a parallela all'asse y, si consideri una qualunque retta
passante per O e per un punto P variabile su a. I due punti A e B che distano k dal punto P, fanno
parte della concoide.
Con GeoGebra è molto semplice procedere alla costruzione:
- Si definiscono due cursori o sliders d e k con valori positivi; d rappresenta la distanza della
retta a dall'origine O e k la distanza che i punti della concoide debbono mantenere da P punto qualsiasi della retta a - Dopo aver disegnato il punto O e la retta a, si definisca il punto P variabile su a
- Si disegni la retta OP e una circonferenza con centro P e raggio k. I due punti di incontro
A e B fra la circonferenza e la rettta per OP sono i due punti cercati della concoide - Con il bottone Luogo di GeoGebra, si defisca il luogo descritto dal punto B al variare di P
ed anche il luogo descritto da A al variare di P

Variando i valori di d e k, si sfrutta la meravigliosa capacità di GeoGebra di cambiare il grafico
della curva in modo quasi istantaneo.
Si può anche ricorrere alle curve parametriche di GeoGebra per disegnare direttamente la concoide.
Le equazioni parametriche della concoide si trovano ad esempio su Wikipedia:
Con GeoGebra queste equazioni possono essere scritte così:
Curva[d + k cos(t), d tan(t) + k sin(t), t, 0,2* π ]
ovvero:
Curva[ Espressione, Espressione, Variabile parametro, Valore iniziale, Valore finale ]
Nella stessa pagina di Wikipedia viene esposta l'interessante dimostrazione relativa alla concoide come
curva che consente di dividere in tre parti uguali un angolo.
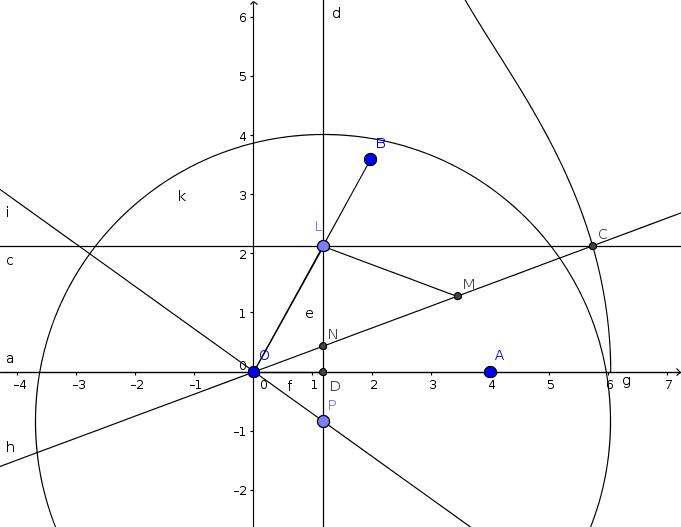
Sia AOB l'angolo di cui si cerca la terza parte. Si prenda L qualunque su OB.
Da L si tracci la parallela e la perpendicolare ad OA.
Il punto di incontro di questa perpendicolare con OA sia D.
Si disegni adesso la concoide definita a partire dal punto O che dista OD dalla retta DL e abbia
parametro dato da 2 OL. In altri termini si può utilizzare il comando Curva visto prima con
d=OD e k=2 OL
Sia C l'intersezione fra la concoide e la parallela per L ad OA.
L'angolo AOC è la terza parte di AOB cercata.
Dimostrazione

Sia N il punto di incontro di DL con OC, ed M il punto medio di NC.
Dato che NLC è rettangolo in L, essendo NC ipotenusa divisa in due parti uguali NM e MC anche
ML=NM=MC.
Per la definizione di concoide, NC è proprio il parametro della curva cioé NC=2 OL e quindi OL=LM
In sostanza si avranno due triangoli isosceli: OLM ed LMC. Si deduce che gli angoli alla base sono uguali:
LOM=LMO e MLC=MCL
Inoltre l'angolo LMO è esterno del triangolo MLC, allora: LMO=2 MCL
Ma quest'ultimo angolo MCL è uguale a COA perchè rette parallele tagliate da una trasversale
formano angoli alterni interni uguali.
In fine essendo l'angolo LOM uguale a LMO=2 MCL, si colclude che l'angolo iniziale AOB è diviso in due parti
di cui una è il doppio dell'altra.