Il rapporto tra f ed a deve essere uguale al rapporto fra a ed (f-a) in base alla
definizione di sezione aurea.
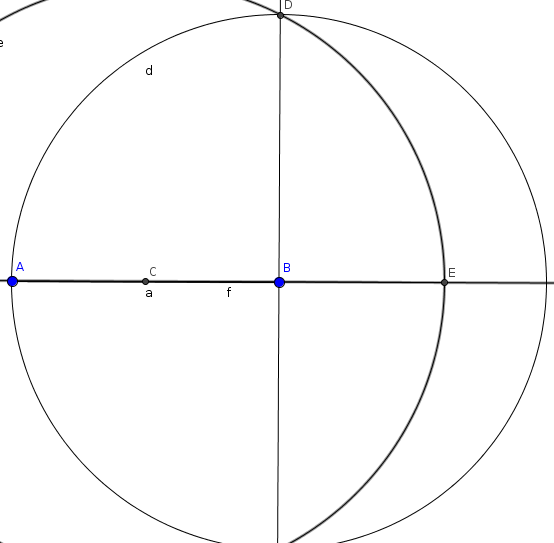
Il segmento iniziale a ha estremi A e B. Si tracci la perpendicolare per B e la retta per A e B.
Disegnamo la circonferenza per A di centro B. Intersezione fra circonferenza e perpendicolare, si trova D.
C è il punto medio di AB. Si disegni la circonferenza di centro C e passante per D.
L'intersezione fra questa ultima circonferenza e la retta per A e B è il punto cercato E.
Il segmento AE di nome f avrà per sezione aurea proprio a, come si può facilmente verificare.
Indichiamo con a anche la misura di AB. Con Pitagora si trova che CD=CE misurerà a∙√(5)/2
Il segmento AE sarà dato da a/2+a∙√(5)/2
Mentre il segmento BE sarà lungo a∙√(5)/2-a/2
Si può così scrivere la proporzione:
(a∙√(5)/2+a/2):a=a:(a∙√(5)/2-a/2)
che è vera.
Costruzione del pentagono
Una volta trovato il segmento f a partire da a si può disegnare il pentagono regolare di lato a e
diagonale f (a è la sezione aurea di f).

Si debbono tracciare 3 circonferenze:
- Una di centro D e raggio f
- Una di centro F e raggio f
- Una di centro G e raggio a, dove G è l'intersezione delle prime due circonferenze
I punti DFIGH saranno i vertici del pentagono.
Lato e diagonale del pentagono regolare
Disegnamo i lati del triangolo DFG: con GeoGebra si può verificare che gli angoli di questo
triangolo sono 72, 72, 36.
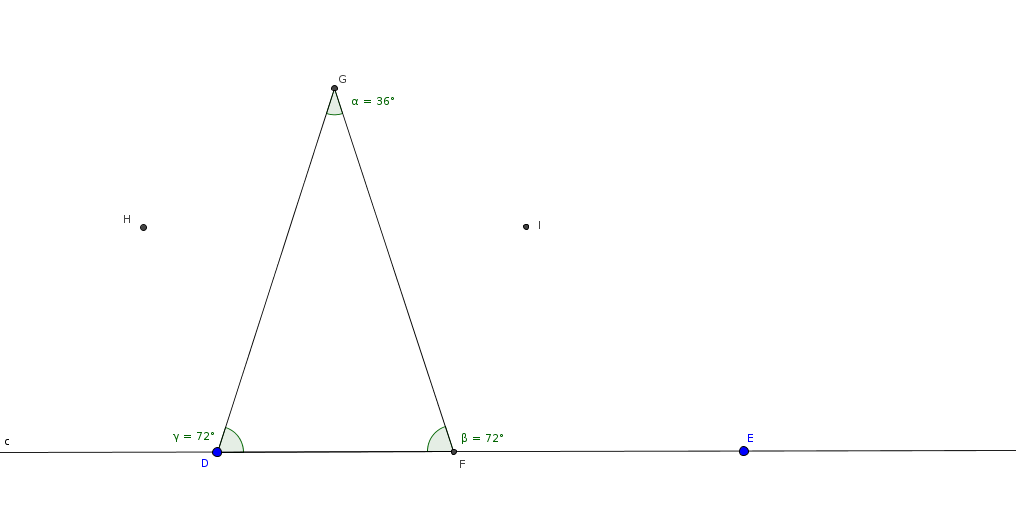
Tracciamo la bisettrice dell'angolo DFG.
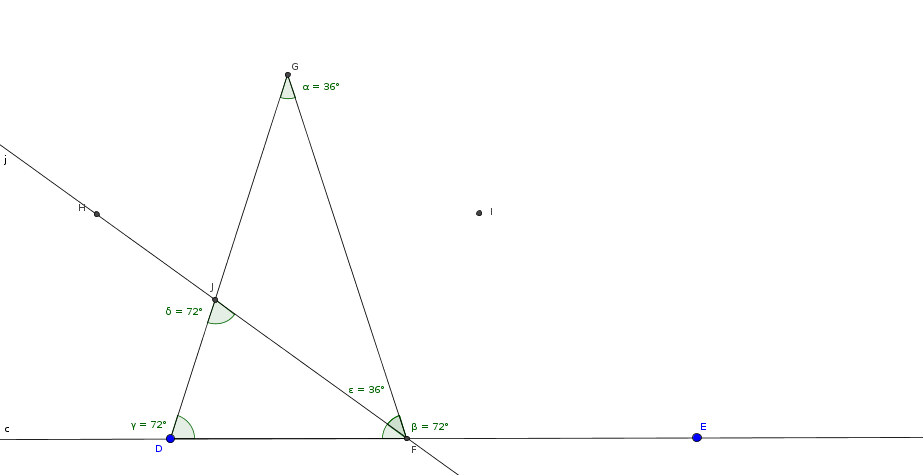
I due triangoli DFG e DFJ sono simili perchè hanno angoli uguali.
DF è uguale a JF ed anche a JG:
DG:DF=DF:DJ
f:a=a:(f-a)
Ovvero il lato a del pentagono regolare è la sezione aurea della sua diagonale.
Angolo al centro e alla circonferenza
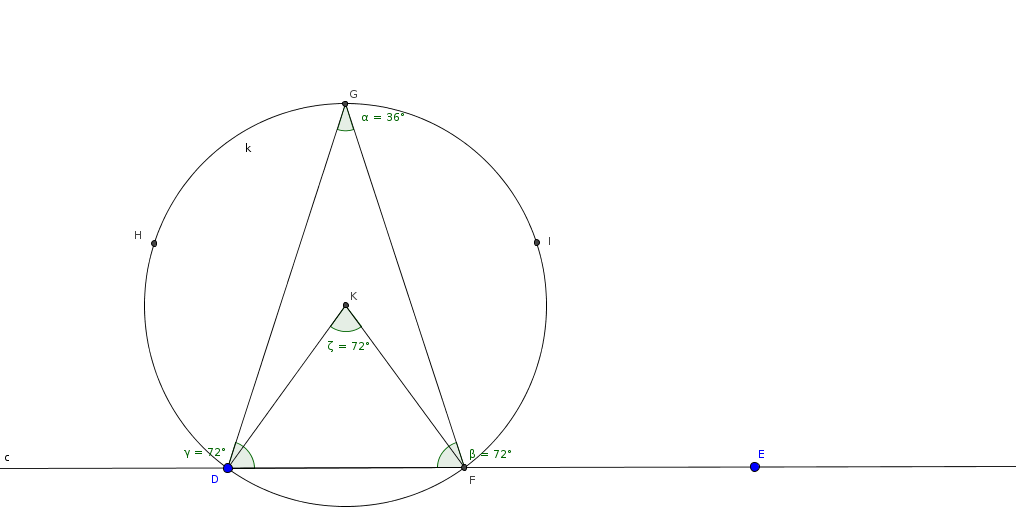
DF è il lato del pentagono regolare quindi l'angolo DKF deve essere 360/5.
Questa proprietà si può applicare all'icosaedro (poliedro regolare di 20 facce triangoli equilateri)
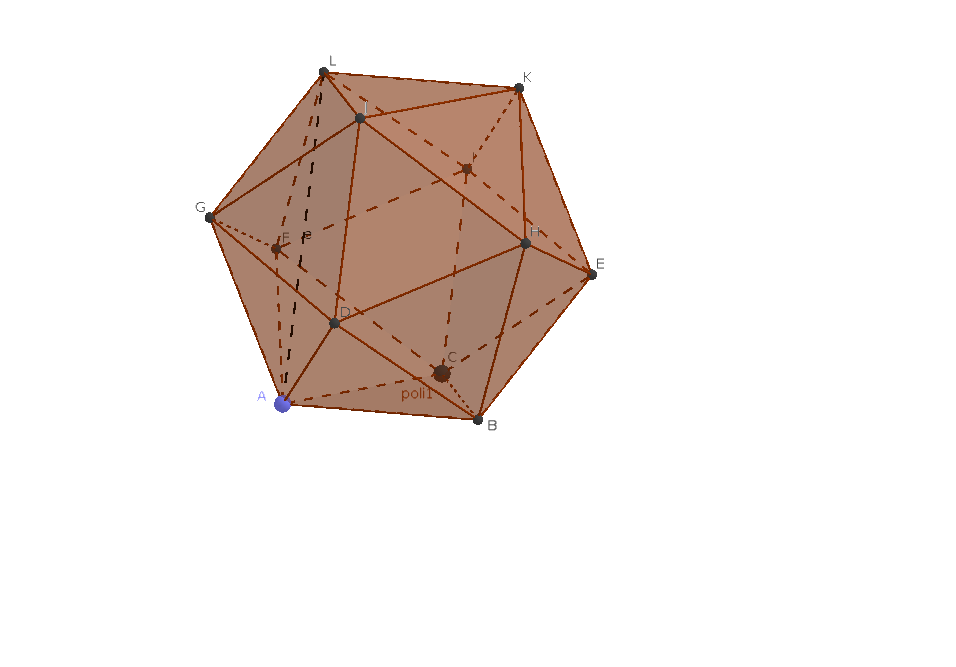
Il segmento AL ha per sezione aurea lo spigolo AB. Infatti AL è la diagonale del pentagono
regolare ADILF.