Prof Calogero Gugliotta

Liceo Scientifico Fermi Menfi

Il comportamento di un Gas ideale può essere descritto o da un modello macroscopico o da un modello microscopico.

Modello macroscopico di un gas ideale

Le proprietà macroscopiche di un gas ideale sono espresse da tre leggi:

1. La legge di Boyle.
   
   Mantenendo fissa la temperatura T e facendo variare la pressione P e il volume V comprimendo il gas del sistema termodinamico mediante il pistone, il prodotto pressione per volume rimane costante
   
   P*V=costante (1)
   
   
   
   
2. Prima legge di Gay-Lussac
   
   Il volume di un gas ideale a pressione costante è direttamente proporzionale alla temperatura assoluta
   
   VµT (2)
   
   
   
   
3. Seconda legge di Gay-Lussac
   
   La pressione di un gas ideale a volume costante è direttamente proporzionale alla temperatura assoluta
   
   PµT (3)
   
   
   

Le tre leggi possono essere espresse da un’unica equazione

Equazione di stato dei gas ideali

P*V=nRT (4)

n è il numero di moli; R=8,31 J/(mol.K)

Modello microscopico di un gas ideale

(Teoria cinetica dei gas)

Vogliamo dedurre la pressione esercitata sulle pareti di un contenitore cubico da un gas ideale racchiuso in esso, riferendoci alla figura sotto.

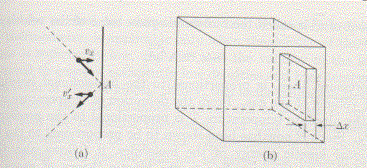
N numero di molecole in un contenitore rettangolare di volume V (area di base A e spessore Dx)

N/V numero di molecole per unità di volume

Consideriamo il volume di area A e spessore Dx a ridosso della parete.

Il numero di molecole contenuto in esso è

(N/V)V=(N/V)ADx (5)

Supponiamo che N₁/V di esse abbiano una componente v_1x di velocità lungo l’asse delle x. Poiché la velocità v_1x è ugualmente probabile che sia positiva o negativa (metà si dirigono verso la parete e metà se ne allontanano) il numero di molecole che colpiranno in un tempo massimo Dt la parete sarà :

(N₁ADx)/2V (6)

In realtà alcune di esse colpiranno la parete un po’ prima trovandosi più vicine di Dx.

Poiché l’intervallo è:

Dx=v_1xDt (7)

sostituendo la (7) nella (6) si ha:

(N₁Av_1xDt)/2V numero di molecole che colpiscono la parete in un tempo Dt

(N₁Av_1x)/2V numero di molecole che colpiscono la parete nell’unità di tempo

Per ognuno di questi urti la quantità di moto trasferita alla parete è:

2mv_1x quantità di moto trasferita ogni urto

La forza media su A è uguale al prodotto tra la quantità di moto trasferita per urto e il numero di urti al secondo:

F₁=( quantità di moto trasferita ogni urto)X(numero di molecole che colpiscono la parete nell’unità di tempo)= 2mv_1x* (N₁Av_1x)/2V=N₁mv_1x²A/V

P₁=F₁/A=N₁mv_1x²/V (8)

Con analogo ragionamento si deduce:

P2=F2/A=N2mv2x^2/V

contributo alla pressione sulla parete da parte delle molecole con componente v2x della velocità

Generalizzando:

P=P₁+P₂+ ………………P_n =m(N₁v_1x² +N₂v_2x²+………..)/V (9)

Se definiamo la velocità quadratica media:

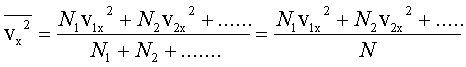
si ha:

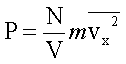(10)

Essendo le tre componenti della velocità quadratica media ugualmente probabili, possiamo infine scrivere:

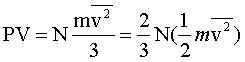(11)

Abbiamo così a disposizione due equazioni per i gas ideali, che sono state ottenute indipendentemente l’una dall’altra, la (4) del modello macroscopico e la (11) della teoria cinetica.

Confrontando queste due equazioni otteniamo:

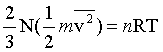(12)

Il prodotto del numero totale N delle molecole per la massa m di ognuna di esse è la massa totale del gas, la quale può essere ottenuta come prodotto del numero n di moli del gas per la massa M di una mole del gas. Cos’ la (12) diventa:

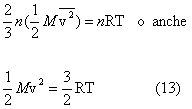
Dividendo i due membri della (13) per il numero di Avogadro N_A si ha infine:

in cui k è la costante di Boltzmann k=R/N_A=1,380*10^-23 J/K

La (14) è un risultato notevole perché mostra che

• la temperatura Kelvin T di un gas è direttamente proporzionale all’energia cinetica media di traslazione delle molecole di un gas;
• tutti i gas, indipendentemente dai volumi, dalle pressioni, dalle masse delle singole molecole o da altre proprietà, hanno la stessa energia cinetica media se sono alla stessa temperatura