
Il Calcolo Continuo
di
Enrico Contenti
Può sembrare bizzarro chiedere a qualcuno se esistono operazioni intermedie tra la somma ed il prodotto. Il fatto è che queste operazioni esistono, anzi ne esiste una gamma infinita.
Supponiamo che s sia la somma dei valori a e b e p il loro prodotto. Ora poniamo in modo convenzionale che la somma sia espressa dal numero 1 ed il prodotto dal numero 2, quindi, fatte queste premesse, possiamo scrivere:
1) Somma s = a [1] b
2) Prodotto p = a [2] b
a questo punto sorge spontanea la domanda, quanto fa c = a [1,5] b ?
Si possono inventare infiniti modi per rispondere a questa domanda e di seguito ne illustrerò alcuni.
Calcolo Continuo Ellittico.
La figura 1 illustra molto chiaramente il modello che si vuole utilizzare per calcolare l'operazione [1,5] e naturalmente tutte le operazioni che vanno da 1 a 2, cioè dalla somma sino al prodotto in modo continuo.
Sull'asse Y poniamo la somma dei due numeri, sull'asse X il segmento del loro prodotto, uniamo le estremità con una curva ellittica. Con un angolo di 0° gradi si ottiene la somma, operazione [1], con l'angolo di 90° gradi il prodotto, operazione [2] e con angoli intermedi le operazioni intermedie tra 1 e 2. In figura l'angolo scelto è di 45° e corrisponde all'operazione [1,5]. Si traccia la retta che parte dall'origine O con l'angolo scelto fino ad incontrare la curva nel punto z. Il segmento oz è il valore che si cercava.
La peculiarità del calcolo ellittico sta nel fatto che qualsiasi operazione tra 1 e 2 da sempre 4, se a e b sono uguali a 2, perché l'ellisse diventa un cerchio.

(Naturalmente l'angolo varia in funzione della operazione scelta.)
Per ottenere il risultato non c'è di meglio che affidarsi al computer che con un breve programma risolve automaticamente il problema. Le equazioni da trovare ed assegnare al programma, in questo caso non sono molto complicate.
s = a+b
p = a*b
delta = 3.14159 / 2
T = operazione - 1
alfa = delta - delta * T
r1 = p ^ 2 * s ^ 2
r2 = (p ^ 2 * (Sin(alfa)) ^ 2) + (s ^ 2 * (Cos(alfa)) ^ 2)
r = (r1 / r2) ^ 0.5 '(risultato)
Calcolo Continuo Lineare.
Nel calcolo continuo lineare ciò che congiunge le due estremità Y1 e X1 è una retta. Le relative equazioni le lascio calcolare a voi. In figura 2 si vede come si presenta questa ipotesi.
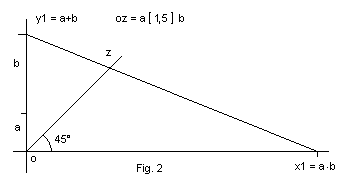
Calcolo Continuo Sinusoidale.
In questa particolare situazione le equazioni da trovare non sono affatto semplici, forse in questo caso si potrebbe tentare di utilizzare le reti neurali. Gli esperti in quel campo potrebbero provare una volta di più le reali capacità di quella straordinaria scoperta.
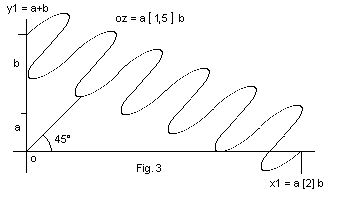
In questo tipo di calcolo le operazioni di rango minore a volte superano i valori di quelle con rango maggiore, altre volte la funzione ha più di un valore.
E' arduo ipotizzare quali tipi di problemi siano in grado di risolvere queste operazioni. Credo che in futuro si troverà una risposta anche a questa domanda. Comunque il primo caso illustrato ci riconduce alla nota funzione che determina il moto dei corpi celesti.