| Siano: |
f : X
® |
|
si dice che: |
"il limite di f(x),
per x che tende a p, è l" |
|
e si scrive: |
|
|
|
| Siano: |
f : X
® |
|
si dice che: |
"il limite di f(x),
per x che tende a p, è l" |
|
e si scrive: |
|
se, per ogni intorno I(l) di l, è possibile trovare un intorno I(p) di p, tale che:
per ogni x Î I(p) Ç X , x ¹ p sia f(x) Î I(l)
A seconda che p e l
siano numeri reali oppure +¥ , -¥
si hanno vari casi particolari, ad esempio:
![]()
pÎ![]() ,
l Î
,
l Î![]()
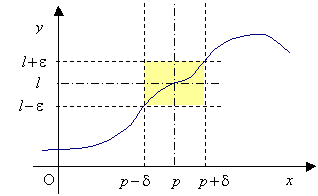
" e
> 0 $ d
> 0 " x Î
X : 0 < | x - p|
< d Þ | f(x)
- l|<e
![]()
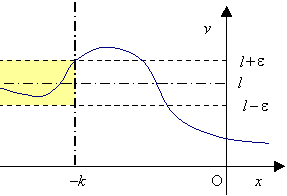
p = -¥, l Î
![]()
" e
> 0 $ k >
0 " x Î X
: x < - k Þ
| f(x) - l| < e
![]()
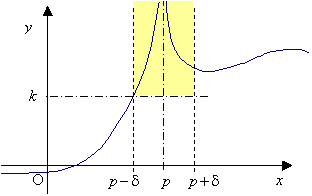
p Î ![]() ,
l = +¥
,
l = +¥
" k
> 0 $ d
> 0 " x Î
X : 0 < | x - p|
< d Þ f(x)
> k
![]()
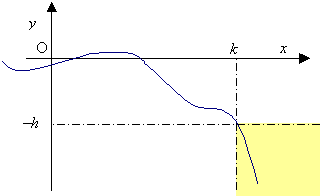
p = +¥ , l = -¥
" h
> 0 $ k >
0 " x Î X
: x > k Þ
f(x) < - h