1     Sapendo che x e y sono due numeri naturali consecutivi con 1fx<yf9, trovare i due numeri in modo che la seguente divisione dia resto 0: (xy + yx)/x

2. Un professore ha una scatola di 1300 penne, e vuole distribuirle in modo equo ai suoi alunni. Così incomincia col dare ad ognuno tante penne quanti ne sono gli alunni. Dopo di che, visto che ne rimangono ancora un bel po', decide di darne altre due ciascuno. Alla fine nella scatola ne rimangono solo cinque, che egli tiene per sé. Quanti sono gli alunni?
   
3. Un commerciante chiede ad un fabbricante d'auto di costruirgli 103 macchine. Il fabbricante però ne costruisce molte di più, perché prima di consegnarle, esattamente un terzo di esse le dà ad un altro cliente. Però, quando conta le macchine rimaste, si accorge che non bastano per soddisfare la richiesta del commerciante. Qual era il numero minimo di macchine che il fabbricante doveva costruire per non avere questo problema?
   
4. Il sindaco di un comune compra un certo numero di alberi e decide di farli piantare ai lati delle vie della sua città. Così pensa di piantare per ogni via tante piante quante sono le stesse vie. Per questo scopo però servono altre 175 piante che egli subito ordina. Alla fine ogni via avrà esattamente un trentesimo del numero delle piante comprate inizialmente. Quante sono le vie della città?
   
5. Un americano compra un certo numero di barche e almeno un quinto di esse le promette a suo nipote. Ma prima di fare il regalo al nipote ne rivende 65 ad un arabo. A questo punto però si accorge che in questo modo non può più mantenere la promessa fatta al nipote. Qual era il numero minimo di barche che doveva comprare per non mancare alla promessa fatta?
   
6. Sapendo che  A,B,C sono cifre dispari, calcolarne i valori e il risultato della seguente operazione:
   

10. Un signore afferma che, stando a casa, un giorno gli è capitato che pur andando a dormire alle otto di sera e essersi svegliato alle sei del mattino del giorno successivo ha dormito per più di 10 ore. E possibile? Perché?    (1-11-99)
    
11. In una campagna vi è un gran numero di uccelli (non importa quanti, ma molti) appartenenti a tre specie diverse. Devono sistemarsi su un albero che conta in tutto 8 rami. Sapendo che ogni ramo può essere occupato da un solo uccello, quante combinazioni di specie di uccelli si possono avere sull'albero, tenendo anche presente che sull'albero devono esserci almeno due specie diverse?
    
12. Un enologo ha a disposizione una gran quantità di vino (non importa quanto, ma molto vino). Ha quattro tipi di vino che vengono sistemati in un determinato numero di damigiane. Tenendo presente che le damigiane possono contenere anche tutte lo stesso tipo di vino, si calcola che le combinazioni possibili dei 4 tipi di vino sistemate per ogni botte sono 16384. Sapendo che ogni damigiana contiene un solo tipo di vino e può contenere al massimo 10 L., quanti litri di vino vengono messi nelle damigiane affinché sia possibile il numero di combinazioni trovato? E quante devono essere le damigiane?
13. Un carcerato, con l'aiuto di un complice libero, studia un piano per evadere dal carcere. Egli è rinchiuso in una cella a pian terreno con una piccola grata che si affaccia all'esterno. Così dice al complice di presentarsi una notte con una macchina ed una corda abbastanza robusta in modo da legarla alle sbarre della grata e con la macchina tirarla affinché si divelta. Al momento dell'evasione, però, il carcerato si accorge che la corda portata dal complice non è adatta allo scopo. Essa, infatti, è spessa 3 cm, lunga 6 m e presenta alle due estremità due rigonfiamenti, che acquistano uno spessore di più di 10cm. Le sbarre della grata, invece, distano l'una dall'altra solo 8 cm, quindi il capo della corda non può passare assolutamente fra le sbarre e non è possibile perciò legare la corda in questo modo. Dopo alcuni secondi però l'astuto carcerato riesce a farlo senza apportare alcuna modifica alla corda ed è finalmente libero. Come ha fatto? (27-5-00)
14. Un geometra chiama un suo allievo gli da un block notes, una penna, un metro e gli dice di andare a rilevare le misure di una vecchia Torre poco lontano da lì. Il giovane allievo, animato da entusiasmo per il compito affidatogli, si mette subito in marcia. Arrivato nel luogo indicatogli dal suo capo si trova davanti una torre altissima situata in una zona desolata, senza alcuna casa o albero attorno. Mentre si appresta ad effettuare le misure si accorge che non c'è alcun accesso per salire sulla torre e il materiale di cui dispone (un piccolo metro) non gli consente di effettuare una misura esatta data l'enorme altezza della costruzione. Così si guarda un attimo attorno, pensa un attimo, effettua le misure e ritorna dal suo capo che gli fa i complimenti. Come ha fatto il giovane a misurare l'altezza della torre? (28-05-00)
15. Dopo una battaglia, almeno il 90% perdette un occhio, almeno il 95% perdette un dente, almeno l’80% perdette un braccio e almeno il 75% perdette una gamba. Quanti almeno perdettero tutti e quattro gli organi?*
16. Due navi lasciano ciascuna un porto allo stesso istante. Una viaggia alla velocità di 35 miglia/ora, l’altra a 45 miglia/ora. La distanza tra i due porti è di 160 miglia. Su una nave è appollaiato un gabbiano che spicca il volo, appena le navi partono, alla velocità di 60 miglia/ora per raggiungere l’albero della seconda nave e appena giuntovi, riparte verso la prima e così di seguito fino a quando le due navi si incontreranno. La domanda è: “quando le navi si incontrano, quante miglia avrà percorso il felice gabbiano?*
17. Le due lancette di un orologio si sovrappongono perfettamente alle ore 12, dopo quanto tempo saranno di nuovo sovrapposte?*
18. Un elastico lungo tre metri è fissato da una parte. Una formica si muove lungo l’elastico percorrendo un metro al minuto. Dopo un minuto l’elastico, partendo da un’estremità, si allunga di altri 3 metri. Questo si ripete alla fine di ogni minuto, finché la formica non raggiunge l’estremità dell’elastico. Assumendo che l’elastico possa essere allungato così tanto, quanto tempo impiegherà la formica per arrivare alla fine?*
19. Qual è quel numero che diviso per 3 dà resto 1, diviso per 5 dà resto 2 e diviso per 7 dà resto 3? E quanti se ne possono trovare almeno tra diciamo i primi 5000 numeri naturali?*

20. Una vecchietta con un canestro pieno di mele va bussando per le case per venderle. Alla signora della prima casa vende la metà delle mele del canestrino + mezza mela. Alla quella della seconda casa vende la metà delle mele rimaste nel canestrino + mezza mela. Infine a quella della terza casa vende la metà delle mele rimaste nel canestrino + mezza mela. A questo punto il canestro è vuoto.>Quante mele c’erano nel canestro all’inizio ?

21. Un magnifico salice è piantato all'interno di un terreno quadrato. La somma delle sue distanze da due lati del quadrato è di 100 m, mentre la somma delle distanze dagli altri due lati è uguale a 120 m. Qual è l'area (in metri quadrati) del terreno?

22. Quanti sono i numeri di tre cifre la cui somma delle stesse tre cifre sia uguale a 9?

23. Un rettangolo è inscritto in un quadrante di cerchio come mostrato in figura. Determinate con esattezza la lunghezza della diagonale AC, sapendo che il cerchio ha raggio unitario.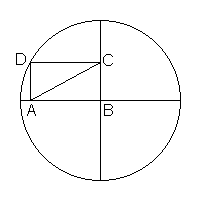

24.  Un imbianchino dipinge una stanza in 1 ora, un altro imbianchino dipinge la stessa stanza in un ora e mezzo, infine un terzo imbianchino dipinge la stessa stanza in 2 ore. Se dipingono tutti insieme la stessa stanza quanto tempo ci mettono?

25.  Tre compari, Giacomo, Giovanni e Pasquale, vivono nella periferia di un paese, ma ciascuno, per il mestiere che fa, si reca di tanto in tanto in città alla fiera. Un bel giorno, per esser precisi era il primo del mese, capita che i tre amici si incontrano per caso al mercato; contenti di essersi ritrovati decidono di festeggiare a modo loro: dinanzi a un bel boccale di vino. Alla fine, quasi brilli, si ripromettono di rivedersi. Ma con perplessità Giacomo afferma: “ehm…io ci ritornerò ogni tre giorni, ho quindi 1/3 di possibilità di ritrovarmi al mercato, come faremo?”; Giovanni: “ed io ogni quattro giorni, ad essere preciso ho 1/4 di possibilità”; mentre Pasquale afferma che potrà esserci solo ogni cinque giorni, quindi ne avrà sì e no 1/5 di possibilità di ritrovarsi al mercato in un determinato giorno. A questo punto i tre sembrano perplessi: “…e quando allora ci rivedremo, se ciascuno torna in giorni diversi, la probabilità di ritrovarci tutti e tre è praticamente senza speranze!” Esclamò addolorato il buon Pasquale. Ma il trattore, che tra l’altro aveva truffato sul conto, pensò: “accidenti io apro bottega ogni due giorni, mi resta solo il 50% di possibilità di beccarli, ammesso che si incontrino!”, ma dopo appena una frazione di secondo, si illuminò di ingegnosa malizia: “ …ma sì, io lo so quando si ritroveranno, e so anche che sarò qui a fregarli di nuovo!”

Come ha potuto l’astuto trattore, pur non disponendo di calendario, in un lampo conoscere con precisione la data dell’incontro dei tre e che in quel giorno di sicuro ci sarebbe stato anche lui?*

26.  

Considerate queste righe di numeri:
1
11
21
1211
111221
312211
13112221
1113213211
Qual è la prossima riga?

Un caloroso  ringraziamento ad un altro   *Gennaro che gentilmente ha contribuito ad arricchire questa sezione del sito con l'aggiunta   di nuovi e divertenti giochi!

Ora tocca a voi: Proponete i vostri giochi

Per conoscere le soluzioni di questi quesiti mandate    un' e-mail al mio indirizzo di posta elettronica, specificando il numero o i numeri delle domande di cui volete la risposta:

BUON DIVERTIMENTO!!!!

Per le RISPOSTE scrivete a:       GENNY77@libero.it