BRANO TRATTO DA « LA GÉOMÉTRIE » DI CARTESIO
Je pourrois
mettre ici plusieurs autres moyens pour tracer et concevoir des lignes courbes
qui seroient de plus en plus composées par degrés à l’infini; mais pour
comprendre ensemble toutes celles qui sont en la nature, et les distinguer par ordre en certains genres, je ne
sache rien de meilleur que de dire que tous les points de celle qu’on peut
nommer géométriques, c’est-à-dire qui tombent sous quelque mesure précise et
exacte, ont nécessairement quelque rapport à tous les points d’une ligne
droite, qui peut être exprimée par quelque équation, en tous par une même; et
que, lorsque cette équation ne monte jusqu’au rectangle de deux quantités
indéterminées, ou bien au carré d’une même, la ligne courbe est du premier et
plus simple genre, dans lequel il n’y a que le cercle, la parabole, l’hyperbole
et l’ellipse qui soient comprises; mais que lorsque l’équation monte jusqu’à la
troisième on quatrième dimension des deux, ou
de l’une des deux quantités indéterminées (car il en faut deux pour
expliquer ici le rapport d’un point à un autre), elle est du second; et que
lorsque l’équation monte jusqu’à la cinquième ou sixième dimension, elle est du
troisìème; et ainsi des autres à l’infini.
Comme si
je veux savoir de quel genre est la ligne EC (fig.8), que j’imagine être
décrite par
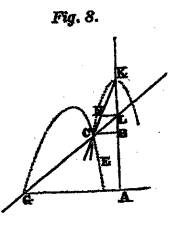
l’intersection
de la règle GL et du plan rectiligne CNKL, dont le côté KN est indéfiniment
prolongé vers C, et qui, étant mu sur le plan de dessous en ligne droite,
c’est-à-dire en telle sorte que son diamètre KL se trouve toujours appliqué sur
quelque endroit de la ligne BA prolongée de part et d’autre, fait mouvoir
circulairement cette règle GL autour du point G, à cause quelle lui est
tellement jointe qu’elle passe toujours par le point L. Je choisis une ligne
droite comme AB, pour rapporter à ses divers points tous ceux de cette ligne
courbe EC; et en cette ligne AB je choisis un point comme A, pour commencer per
lui ce calcul. Je dis que je choisis et l’un et l’autre, à cause qu’il est
libre de les prendre tels qu’on veut; car encore qu’il y ait beancoup de choix
pour rendre l’équation plus courte et plus aisée, toutefois en quelle façon
qu’on les prenne, on peut toujours faire que la ligne paroisse de même genre,
ainsi qu’il est aisé à démontrer. Après cela prenant un point à discrétion dans
la courbe, comme C, sur lequel je suppose que l’instrument qui sort à la
décrire est appliqué, je tire de ce point C la ligne GB parallèle à GA, et
pourceque CB et BA sont deux quantités indéterminées et inconnues, je la nomme
l’une y e l’autre x; mais afin de trouver le rapport de l’une à
l’autre, je considère aussi les quantités connues qui déterminent la
description de cette ligne courbe, comme GA, que je nomme a, KL que je
nomme b, et NL, parallèle à GA, que je nomme c; puis je dis,
comme NL est à LK, ou c à b, ainsi CB ou y est à BK, qui
est par conséquent 
: et BL
est 
, et AL est 
. De plus, comme CB est à LB, ou y à 
, ainsi GA ou a est à LA ou 
; de façon que, multipliant la seconde per la troisième, on
produit 
qui est égale à 
, qui se produit en
multipliant la première par la dernière: et ainsi l’équation qu’il falloit
trouver est
de
laquelle on connoit que la ligne EC est du premier genre, comme en effet elle
n’est autre qu’une hyperbole.