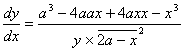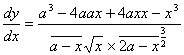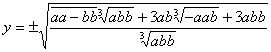E S E M P I O   I

 

75. Sia la curva dell’equazione 2ax - xx = yy, e si voglia sapere, a quale punto dell’asse dell’ascisse x corrisponda la massima ordinata y, e cosa essa sia.

Differenziata l’equazione, sarà 2adx - 2xdx = 2ydy, cioè   . Facendo la supposizione che dy = 0, dovrà essere zero il numeratore della frazione, e però sarà a – x = 0, onde x = a; adunque la massima ordinata corrispondente a quell’ascissa, che sia uguale ad a; sostituito questo valore in luogo di x nella proposta equazione, sarà 2aa – aa = yy, e cioè y = ± a; la massima ordinata adunque positiva, e negativa è uguale ad a. Facendo la supposizione di dy = ¥, dovrà essere zero il denominatore della frazione, e però sarà y = 0, sostituito pertanto questo valore  in luogo di  y nella proposta equazione,  avremo x = 0, ed x = 2a; vale a dire, che x = 0 sarà la minima, ed x = 2a la massima; o più propriamente, che quando sia x = 0, ed x = 2a, essendo infinita la dy rispetto alla dx, la sottotangente sarà nulla, cioè la tangente parallela alle ordinate y.

 

 

E S E M P I O   I I

 

76. Sia la curva dell’equazione xx – ax = yy. Differenziando sarà  . La supposizione di dy = 0 ci dà , ma sostituito questo valore in luogo di x nella proposta equazione, la y si trova immaginaria, dunque la curva non â ordinata, che a tale ascissa corrisponda, e però molto meno avrà massima o minima. La supposizione di dy = ¥, cioè di dx = 0, vale a dire, che la tangente sarà perpendicolare all’asse delle ascisse x nel punto, in cui è y = 0, il quale corrisponde alle due ascisse x = 0, ed x = a, poiché sostituito in luogo di  y il zero nella proposta equazione, sarà xx – ax = 0, e però x = 0, ed x = a .

 

 

E S E M P I O   I I I

 

77. Sia la curva dell’equazione 2axy = a3 + axx –bxx, in cui le x sono le ascisse,  y le ordinate. Differenziando sarà 2axdy + 2aydx = 2axdx – 2bxdx, e però  . La supposizione di dy = 0 ci dà  , e sostituito questo valore nell’equazione proposta, sarà   , cioè ,  ed , massima , o minima ordinata. E poiché abbiamo , fatta la sostituzione del valore della y, sarà  , ascissa, a cui corrisponde la ritrovata massima , o minima ordinata. La supposizione di dy = ¥, o sia di dx = 0 ci dà ax = 0, cioè x = 0 , e fatta la sostituzione nella proposta equazione, sarà a3 = 0, ma implica, che una quantità data finita sia zero, adunque la curva non averà altri massimi, o minimi dai ritrovati nella prima supposizione, i quali per l’ambiguità de’ segni sono due, ed eguali; uno positivo, che corrisponde all’ascissa positiva, l’altro negativo, che corrisponde all’ascissa negativa.

 

78. Ci dà il metodo confusamente i massimi, e minimi, né in forza di esso si possono distinguere gl’uni dagl’altri, si riconoscono però quando sia noto l’andamento della curva; ma senza tale notizia si può procedere così . Si assegni all’ascissa dell’equazione data un valore per poco maggiore, o minore di quello, che corrisponde alla massima, o minima ordinata, di cui si tratta, ed il valore dell’ordinata, che indi nasce, scioglierà il quesito; poiché se sarà maggiore di quello somministratoci dal metodo, la questione sarà de’ minimi; ed all’opposto essendo, sarà de’ massimi. La curva adunque di quest’esempio avrà due minimi.

 

E S E M P I O   I V

 

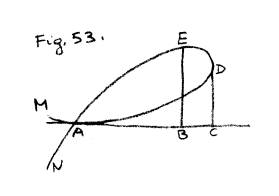
79. Sia la curva MADEAN ( Fig. 53. ) dell’equazione x3 + y3 = axy, AB = x,  BE = y. Differenziando si averà

 , e però facendo la supposizione di dy = 0, sarà  , e fatta la sostituzione di questo valore nella data equazione, si trova  , quindi poiché , sarà = BE la massima ordinata della curva, la quale corrisponde all’ascissa  

= AB. La supposizione di dx = 0 ci darà , e fatta la sostituzione nell’equazione data, sarà , quindi la massima AC, cui corrisponde y = CD =, che è tangente nel punto D.

 

80. Ma prima di passare più avanti con gl’esempj , è necessario prevenire un caso, che suole alcuna volta succedere, ed è che tanto la supposizione di dy = 0, quanto quella di dy = ¥ ci fornisca un medesimo valore dell’ordinata, o dell’ascissa, ed è in tale caso che non si determina alcun massimo o minimo, ma bensì un punto di intersecazione, o d’incontro di due rami della curva . E la ragione è evidente, imperciocchè essendo  eguale ad una frazione, se dal numeratore si ricava lo stesso valore della x, per esempio, che si ricava dal denominatore, quello valore, o radice sostituita renderà nullo l’uno e l’altro, e però in tal punto di curva sarà , ma si è veduto di sopra al num. 69., che indica sempre l’incontro di due rami di curva , adunque ec.

 

 

E S E M P I O   V

 

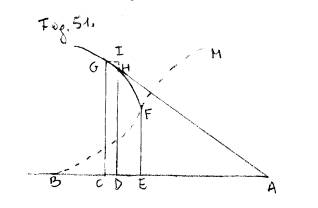
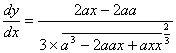81. Sia la curva GFM ( Fig. 51.) la Parabola cubica dell’equazione  y – a =, BE = EF = a, BC = x, CG = y . Differenziando sarà . La supposizione di dy = 0 ci dà x = a; la supposizione di dy = ¥ ci

 

dà parimenti x = a, adunque la curva â un punto d’incontro F, che corrisponde all’ascissa x = a, ed alla minima ordinata y = a, che si cava dalla proposta equazione, sostituito in luogo di x il suo valore.

Sia la stessa equazione, ma libera da’ radicali, cioè ; differenziando sarà  . La supposizione di  dy = 0 ci dà x = a, e posto questo valore nella proposta equazione, si ricava y = a , adunque x = a, ed y = a ci danno il punto F, che è il punto d’incontro, o contatto de’ due rami GF, FM, e nello stesso tempo la minima y.

Ma se opereremo sopra l’equazione , che esprime il solo ramo GF  ( esprimerebbe l’altro ramo FM) avremo  .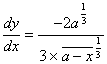

La supposizione di dy = 0 nulla ci fa sapere; la supposizione di  dy = ¥ ci dà x = a, e però y = a, ed il punto F in questo caso ci fornisce un massimo rispetto alla x, ed un minimo rispetto alla  y.

 

82. Dissi, che la supposizione di dy = 0 , che ci dà  nulla ci fa sapere, intendendo rispetto ai massimi finiti, perché comprendendo anco gl’infiniti, ella ce ne somministra due. Se , sarà dunque a = 0, e sostituito questo valore nella proposta equazione , sarà essa , cioè , e però x, ed y infinite. Due sono i massimi , servendo uno al ramo FG , l’altro al ramo FM , poiché posta a = 0 , l’equazione ambedue gli esprime.

Nascerà generalmente questo caso ogni qual volta la supposizione di dy = 0 , o di dy = ¥ ci dia un’espressione finita costante, o un divisore costante eguale al zero, il quale valore sostituito nell’equazione proposta , non porti o immaginario , o contradizione; e la ragione si è che una quantità finita non può essere presa per zero, se non rispetto a quantità infinita.

 

 

E S E M P I O   V I

 

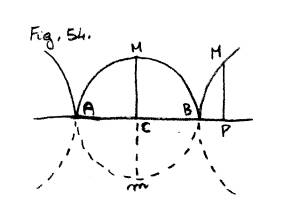
83. Sia la curva (Fig. 54. ) dell’equazione , AB = a;  AC, o AP = x; CM , o PM = y ; differenziando

sarà  . La supposizione di dy = 0 ci dà tre valori di x, cioè x = 0,  x = a, ; il valore x = 0 sostituita nella proposta equazione rende y = 0, il valore x = a rende y = 0 , il valore   rende . La supposizione di  dy = ¥ ci dà y = 0, adunque la y â  il medesimo valore nell’una, e nell’altra supposizione, quando sia x = 0,  ed x = a, quindi i punti A , B saranno punti d’incontro

de’ rami della curva, ed  darà la massima ordinata , o Cm . Il luogo del sopra posto esempio può chiamarsi luogo doppio, il quale nasce dall’essere alzata al quadrato l’una, o l’altra delle due semplici formole ax – xx = yy, al circolo, o pure xx – ax = yy, all’iperbola. Quindi non sarebbe bastato il ridurre l’equazione al semplice circolo, o alla semplice iperbola, ma era necessario avere mira alla complicazione delle dette curve fra loro.

 

 

E S E M P I O   V I I

 

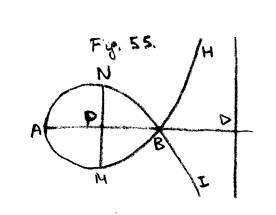
84. Sia la curva della Fig. 55. , la di cui equazione , AP = x, PM = y, AD = 2a. Differenziando sarà

 , cioè  . Prima di andare più avanti osservo, che tanto il numeratore della frazione , quanto il denominatore è divisibile per a - x ; adunque , e nella supposizione di dy = 0 , e in quella di dy = ¥ si averà a – x = 0, cioè x = a, che sostituito ci dà y = 0, e però la curva avrà un nodo nell’asse al punto B, fatta AB = a. Fatta per tanto la divisione, sarà . La supposizione di dy = 0 ci dà ;

il valore  non serve, perché sostituito nell’equazione proposta rende immaginaria la ordinata, la quale è generalmente immaginaria, qualora si assuma x maggiore di 2a, come manifestamente si vede. Sostituiamo perciò l’altro valore

 , ci dà 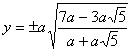. Fatta adunque  , saranno PM, PM le massime ordinate, positiva l’una, e negativa l’altra, ed .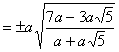

La supposizione di  dy = ¥ ci dà x = 0, ed x = 2a; sostituiti questi valori nell’equazione proposta si averà y = 0, ed dy = ¥; vale a dire, che presa x = 0, cioè nel punto A, la tangente sarà parallela alle ordinate PM, e presa x = 2a = AD, la ordinata sarà infinita, cioè asintoto della curva rispetto ai rami BH , BI .

 

 

E S E M P I O   V I I I

 

85. Sia la Concoide dell’equazione . Differenziando sarà .

Nel primo Libro al num. 239. sono stati da me considerati tre casi di questa curva; il primo quando sia a = b ; il secondo quando sia b minore di a ; ed il terzo quando b sia maggiore di a .

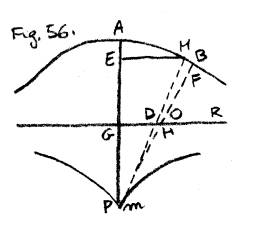
Rispetto al primo caso: la curva sarà quella della Fig. 56., e l’equazione  , presa GA = GP = a, GE = x, EM = y; e differenziando,  . La supposizione di dy = 0 ci dà il numeratore uguale a zero, cioè ; e però x = - a, il quale valore, sostituito nell’equazione della curva, ci dà y = 0. La supposizione di dy = ¥ ci dà il denominatore eguale al zero, cioè , e però x = 0, x = - a, ed x = a; ma il valore il valore x = - a si è trovato anche nella supposizione di dy = 0, adunque

quando sia x = - a, cioè presa GP = a, la curva averà nel punto P un’incontro di due rami.

Il valore x = a sostituito nell’equazione ci dà y = 0, adunque la medesima x sarà = a = GA, a cui corrisponde y = 0. Il valore x = 0 sostituito ci dà y = ¥; adunque per lo punto G, per cui x = 0 , condotta una  parallela alle ordinate, toccherà la curva in infinita distanza, vale a dire, sarà un’asintoto [sic].

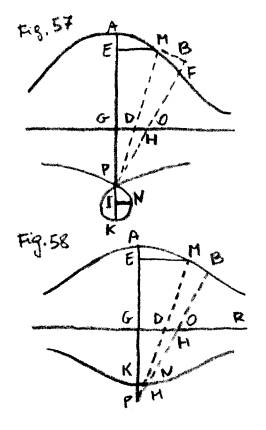
Rispetto agli altri due casi: ( Fig. 57. 58. ) sia GA = GK = a, GP = b, ed il resto come sopra. La supposizione di dy = 0 ci darà – x4 – bx3- aabx-  aabb = 0, cioè , e  però x = -b, .

La supposizione di dy = ¥ ci darà , cioè , e però x = 0 , x = -b , x = a , x = - a .

Il valore x = - b, che nel secondo caso sostituito nell’equazione rende y = 0, ci viene somministrato da ambedue le supposizioni, adunque ( Fig. 57. ) presa GP dalla parte de’ negativi , ed = -b , il  punto P sarà un’incontro [sic], o sia una intersecazione di due rami di curva. Lo stesso valore x = - b, sostituito nell’equazione della curva   , ci dà nel terzo caso negativo il radicale, per essere b maggiore di a , e però immaginaria la curva, quindi a nulla serve.

Il valore , sostituito nell’equazione della curva, ci dà   , cioè immaginaria pure, quando sia b maggiore di a (Fig. 58. ), e però similmente a nulla serve in questo terzo caso; ma ci dà y reale quando sia b minore di a, e però ( Fig.

57. ), fatta ,sarà IN la massima ordinata 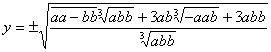. Il valore x = 0 ci dà y = ¥, cioè asintoto; il valore x = ± a ci dà y = 0, cioè la tangente ne’ punti A , K parallela all’ordinate.

 

 

E S E M P I O    I X

 

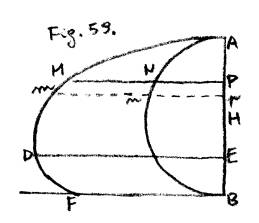
86. Sia la mezza Cicloide abbreviata AMF ( Fig. 59.), chiamata AB =2a, BF = b; AP = x, PM = z, la semiperiferìa ANB = c, l’arco AN = q; sarà , e per la proprietà della curva, è ANB , BF :: AN , NM ; cioè

c , b :: q , ; dunque . Differenziando, ; ma condotta mp infinitamente prossima ad MP, sarà , quindi fatta la sostituzione nell’equazione, avremo . La supposizione di dz = 0 ci dà . Se adunque H sia il centro del circolo, presa HE eguale alla quarta proporzione della semiperiferia ANB, della retta BF, e del raggio, la corrispondente ordinata sarà la massima, che si cerca.

La supposizione di dz = ¥ ci dà x = 0, ed x = 2a, vale a dire, che ne’ punti A, F la tangente sarà parallela alle ordinate.

 

INDIETRO