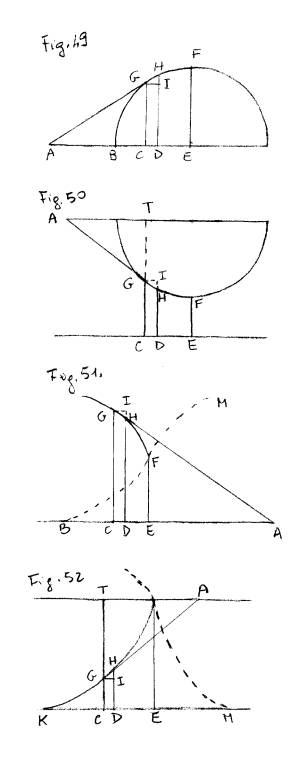
Del Metodo de’ Massimi, e Minimi
72. Se in una curva qualunque, le di cui
ordinate sieno parallele, crescendo le ascisse BC (Fig. 49. 50. 51., e 52.) continovamente,
cresca altresì l’ordinata CG fino ad un certo punto E dopo di cui
vada calando, o non vi sia più ordinata alcuna; o pure al contrario crescendo
l’ascissa, l’ordinata CG vada continovamente calando fino ad un certo
punto E, dopo di cui, o cresca, o più non vi sia; l’ordinata EF
si chiama la Massima, o la Minima.
|
|
Alla curva GHF sia EF la
massima delle ordinate (Fig. 49.), o la minima (Fig. 50.);
presa una qualunque ascissa BC, e condotta l’ordinata CG, al
punto G s’intenda essere tangente GA, e DH infinitamente
prossima a CG; chiamata BC = x, CG = y, e fatta GI
parallela a BC, sarà GI = CD = dx, HI = dy. Poiché sono
simili i triangoli ACG, GHI nella Fig. 49., sarà AC,
CG :: GI, IH; e poiché sono simili i triangoli ATG, GHI
nella Fig. 50., sarà AT, TG :: GI, HI. Ciò posto,
si finga che l’ordinata GC s’accosti sempre parallela a se stessa alla
massima, o minima ordinata EF; egli è chiaro, che accostandosi CG
ad EF, la sottotangente AC, o AT si farà sempre maggiore
per modo, che quando CG cada sopra la EF, la tangente si farà
parallela a BC, e per conseguenza la sottotangente sarà infinita. In
questo caso adunque avrà AC a CG, o AT a TG
ragione infinitesima, rimanendo CG quantità finita; ma poiché è sempre
AC, CG, o AT, TG :: GI, HI, averà anco GI
ad HI ragione infinita, e però sarà dy nulla rispetto alla dx,
cioè dy =0 nel punto della massima, o minima ordinata. Sia la curva GHF, (Fig. 51.,
e 52.) EF la minima delle ordinate (Fig. 51.), o la
massima (Fig. 52.); presa pure una qualunque ascissa BC, e
condotta l’ordinata CG, la tangente
GA, DH infinitamente prossima a CG, e GI
parallela a BC, e chiamate BC = x, CG = y, sarà GI =
CD = dx, IH = dy. Per i triangoli simili ACG, GIH,
sarà ( Fig. 51. ) AC, CG :: GI, IH ; e per
i triangoli simili ATG, GIH, ( Fig. 52. ) sarà AT,
TG :: GI , IH. Accostandosi dunque l’ordinata CG sempre
parallela a se stessa alla massima, o minima ordinata, la sottotangente AC,
o AT si farà sempre minore per modo, che quando CG cada sopra
la EF, la tangente sarà normale a BC, e per conseguenza nulla la
sottotangente. In questo caso adunque averà AC a CG , o AT
a TG la ragione del nulla alla quantità finita, e però essendo della
stessa ragione GI ad IH, sarà dx nulla rispetto alla dy,
cioè dy = ¥ nel punto della massima,
o minima ordinata. Adunque la formula generale per le massime, o minime
ordinate sarà dy = 0, o pure dy = ¥ . 73. Data adunque l’equazione della curva,
di cui si cerca la massima, o la minima ordinata, si dovrà differenziare, per
ritrarne il valore della frazione, o rapporto |
figura di ordinata, se nell’altra
supposizione la faceva la y. Che se nè la prima supposizione di dy
= 0 , nè la seconda di dy = ¥ ci fornirà valore alcuno
reale della y, si dovrà concludere, che la proposta curva non â né
massimi, né minimi.
74.
Serve questo metodo per avere una compiuta, ed efatta idea delle curve; per
ricavare, in quali punti le tangenti sieno parallele agl’assi conjugati ec. Ma
oltre ciò si applica ad infinite questioni, che in tale proposito possono farsi
sì geometriche, come fisich ; tale sarebbe il ricercare fra gl’infiniti parallelepipedi
di una data solidità, quale sia quello, che abbia la minima superficie; siccome
il ricercare fra le infinite vie, che può tenere un mobile, per giugnere da un
punto all’altro non posto nella medesima
verticale, quale sia quella, che sarà trascorsa nel minimo tempo con
data legge di moto, ed altre simili . In tali questioni ritrovata l’espressione analitica di ciò,
che si vuole essere un massimo, o un minimo, si ponga uguale a y, e
fatta la differenziazione, si proceda avanti con le date regole .
[Nota.
Ho cercato di riprodurre le figure dell’edizione inglese del testo in esame il
più fedelmente possibile]