



1. LA TECNICA DELL’ENUMERAZIONE è la tecnica che guida alla progettazione di algoritmi che eseguono una visita sistematica dello spazio di ricerca allo scopo di individuare, se esiste, la soluzione ad una istanza del problema in esame. Per utilizzare questa tecnica dobbiamo definire, per lo spazio di ricerca:
a) Un metodo per stabilire il primo elemento (dello S. di R.) da considerare.
b) Un metodo per stabilire, dato un elemento, quello successivo da considerare.
c) Un metodo per verificare se tutti gli elementi sono stati considerati.
Un esempio di algoritmo enumerativo è la Ricercasequenziale( ). In questo caso di ricerca di un elemento in un vettore, lo spazio di ricerca ha dimensioni lineari rispetto alla dimensione dei dati di ingresso quindi un’efficienza accettabile. Esistono però spesso algoritmi per i quali la dimensione dello spazio di ricerca è elevata (esempio esponenziale) rispetto alla dimensione dei dati di ingresso.
Mentre per quanto riguarda la ricerca, lo spazio di ricerca viene visitato fino all’elemento cercato e viene visitato tutto solo nel caso peggiore, (e cercato nella n-esima posizione o ricerca con insuccesso) nel caso di un problema di ottimizzazione lo spazio di ricerca deve quasi sempre essere ( vedi caso in cui si ricerchi il minimo in un insieme M di interi non negativi, in questo caso la soluzione ottimale è 0 e la visita s’interrompe appena incontrato questo valore) obbligatoriamente visitato per intero.
1. considera il primo elemento x dello spazio di ricerca;
2. se a(x)=true, allora fornisci 0(x) come risultato;
3. se tutti gli elementi dello spazio di ricerca sono stati considerati, allora fornisci ^ (risposta negativa) come risultato;
4. altrimenti considera come nuovo x l’elemento dello spazio di ricerca successivo rispetto a x, e torna al passo 2.

1. considera il primo elemento x dello spazio di ricerca;
2. se a(x)=true e x è la prima soluzione trovata oppure se a(x)=true e x è migliore dell’attimo corrente, poni l’ottimo corrente peri a x;
3. se tutti gli elementi dello spazio di ricerca sono stati considerati, allora fornisci ^ come risultato se non sono state trovate soluzioni ammissibili, oppure o(y), dove y è l’ottimo corrente;
4. altrimenti considera come nuovo x l’elemento dello spazio di ricerca successivo rispetto a x, e torna al passo 2.

La complessità asintotica nel caso peggiore di un algoritmo enumerativo è ovviamente legata alla dimensione dello spazio di ricerca, che deve interamente essere visitato.
ENUM(x)= CINIZ(n)+CPREP(n)+dimSR(n)*CESP(n)
dove:
· DimSR(n) è la dimensione dello spazio di ricerca;
· CINIZ(n) è il costo dell’inizializzazione dell’esploratore, prima della fase di visita dello spazio di ricerca
· CPREP(n) è il costo della preparazione dell’output, dopo la fase di visita dello spazio di ricerca;
· CESP(n) è il costo delle operazioni che devono essere condotte in corrispondenza di ogni elemento dello spazio di ricerca;
NOTA: una tecnica per definire un ordinamento su uno spazio di ricerca è quello di rappresentare lo spazio di ricerca mediante un vettore di n componenti in cui ogni elemento assume valori da 0 a m e considerare tutti le eventuali permutazioni nel seguente modo: considerare ogni vettore, raffigurante una permutazione, come un numero di n cifre in base m+1,cioè un numero in cui ogni cifra può assumere un valore da 0 a m. La prima configurazione corrisponde al numero composto da tutti 0, e l’ultima da tutte cifre pari a m. Data una configurazione X[n], la successiva si ottiene 1 al numero rappresentato da X. Per fare ciò, si analizzano le cifre iniziando dalla meno significativa alla ricerca di una cifra diversa da m. Durante l’analisi tutte le cifre pari ad m vengono poste a 0. Se si incontra una cifra diversa da m, la si incrementa di 1, altrimenti significa che abbiamo tentato di calcolare la configurazione successiva all’ultima.
2. LA TECNICA DI BACKTRACKING estende la ricerca esaustiva (la si può considerare come un raffinamento della tecnica enumerativa) nella risoluzione di problemi di ricerca attraverso l’introduzione di alcuni controlli per verificare il più presto possibile se una soluzione in via di costruzione soddisfi o no le condizioni di ammissibilità in modo da ridurre lo spazio di ricerca. Nello specifico la tecnica consiste nel considerare lo spazio di ricerca come costituito da diverse componenti e ad ogni stadio viene scelta una componente. Si verifica poi che ad ogni stadio i non vengano violate le condizioni di ammissibilità, se ciò succede allora si giunge alla conclusione che la “soluzione parziale” così generata non può condurre a nessuna soluzione, perché qualsiasi suo completamento viola i vincoli del problema,(qui la restrizione dello spazio di ricerca). Quindi si sceglie l’elemento successivo, se non vi è nessun elemento che permetta di non violare i vincoli si ritorna allo stadio precedente i-1 (backtacking) a questo punto si ripete la procedura allo stadio i-1 come allo stadio i. L’algoritmo termina quando si è arrivati alla soluzione (quando si termina l’n-esimo stadio senza che si siano violati i vincoli) oppure quando si fa backtracking fino all’elemento iniziale (alla radice) e siano state scelte tutte le componenti allo stadio iniziale.
L’algoritmo può essere schematizzato con un albero di ricerca dove la radice è il primo elemento scelto, i nodi figli della radice sono gli elementi che si possono scegliere al secondo stadio e così via fino ad arrivare alle foglie che rappresentano lo spazio di ricerca. Quindi se ad un determinato stadio scegliamo un elemento per cui la soluzione parziale viola i vincoli di ammissibilità del problema, allora possiamo ignorare tutto il sotto-albero che ha come radice il nodo raffigurante lo stesso elemento, riducendo così lo spazio di ricerca. Quando si fa Backtracking si passa dal livello i al livello i-1, cioè si torna al padre del nodo corrente.

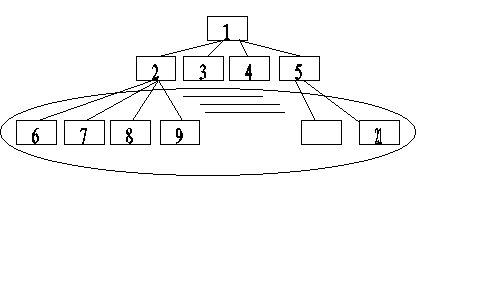
1. l’algoritmo si comporta come se si effettuasse una visita in profondità dell’albero (ad esempio visita anticipata) Bi. Ogni volta che si analizza un nodo, si applica la funzione di controllo a quel nodo. Se la funzione restituisce true, allora il nodo e tutto il sotto-albero viene abbandonato;
2. Se il problema è di ricerca, la visita termina quando si incontra una soluzione,cioè quando su una foglia la funzione di controllo restituisce false, oppure quando tutti i nodi sono stati visitati.
3. Se il problema è di ottimizzazione, l’algoritmo utilizza una variabile, chiamata ottimo corrente. L’agoritmo non si ferma quando trova la 1° soluzione ma prosegue aggiornando opportunamente tale variabile. In più, l’algoritmo fa backtracking anche quando si è sicuri che tutti i completamenti possibili di tale soluzione parziale, anche se non violano le condizioni di ammissibilità, non sono migliori dell’ottimo corrente;

Definito X[n] come il vettore contenente la soluzione (quindi trovato il modo di rappresentare la soluzione in un vettore), per risolvere un problema con la tecnica di Backtracking basta costruire una class risolviproblemaspecifico derivata dalla classe ProblemaBack<T> (dove T è il tipo dell’elemeto X[i] della soluzione) in cui: viene definito un costruttore che inizializzi in maniera opportuna sia i campi della classe base cha quelli della classe derivata; vengono ridefinite le funzioni virtuali pure void PrimoValore ( ), void SuccValore (card k), bool VerificaVincoli(card k). Fatto ciò nel main() definiamo un oggetto R di tipo risolviproblemaspecifico , invochiamo la funzione R.risolvi, e R.soluzione ci restituirà il vettore con la soluzione.
I vantaggi di questa tecnica rispetto alla ricerca esaustiva non possono essere apprezzati con la nostra usuale misura asintotica di complessità poiché nel caso peggiore la tecnica si comporta allo stesso modo di quella esaustiva. Infatti se la funzione di controllo restituisce sempre false, allora il costo BTR(n) dell’algoritmo applicato ad un’istanza del problema di dimensione n può essere espresso come:
BTR(n)= CINIZ(n)+CPREP(n)+dimAR(n)*CESP(n)
dove:
| dimAR(n) è la dimensione dell’albero di ricerca, ovvero il numero dei suoi nodi; | |
| CINIZ(n) è il costo dell’inizializzazione dell’esploratore, prima della fase di visita dell’albero di ricerca; | |
| CPREP(n) è il costo della preparazione dell’output, dopo la fase di visita dell’albero di ricerca; | |
| CESP(n) è il costo delle operazioni che devono essere condotte in corrispondenza di ogni nodo dellabero; |
Ciò significa che la maggior efficienza dell’algoritmo di Backtracking rispetto all’algoritmo enumerativo non è evidenziata dall’analisi della complessità nel caso peggiore ma una maggiore efficienza emergerebbe se effettuassimo un’analisi di complessità nel caso medio, attribuendo un peso ad ogni configurazione in base alla probabilità che tale configurazione si verifichi.
3. LA TECNICA GOLOSA viene spesso utilizzata per la progettazione di algoritmi per la risoluzione di problemi di ottimizzazione in cui, dato un certo numero di oggetti come input, bisogna scegliere un sottoinsieme di essi che ottimizzi una funzione obbiettivo rispettando un certo numero di vincoli.
La tecnica golosa effettua la scelta di un elemento alla volta sulla base di qualche criterio di scelta dell’elemento che sembra il più conveniente. Analogamente alla tecnica di Backtracking, la tecnica golosa esegue il processo di costruzione in stadi. Diversamente dalla tecnica di Backtracking, però, la tecnica golosa si basa sui seguenti principi:
· Ad ogni stadio i, per la componente i-esima viene scelto il valore che, tra quelli ammissibili, risulta il migliore rispetto ad un determinato criterio; ovviamente, per problemi di ottimizzazione, tale scelta è dipendente dalla funzione obiettivo del problema; la scelta avviene sulla scorta delle informazione disponibili a quello stadio.
· Una volta fatta la scelta per la i-esima componente, si passa a considerare le altre componenti senza più tornare sulla decisione presa
Lo schema di un algoritmo goloso presuppone che l’algoritmo acquisisca la rappresentazione di una istanza del problema, e stabilisca un metodo per costruire un oggetto s dello spazio di ricerca in diversi stadi.
1. poni i pari a 1 e inizializza s;
2. determina l’insieme A dei valori ammissibili per la componete i-esima di s, e, se A non è vuoto, scegli il migliore in A, rispetto al criterio di preferenza fissato;
3. se l’i-esimo stadio è l’ultimo allora termina e restituisci o(s) come risultato;
4. altrimenti incremente i di 1 e torna al passo 2.

In un algoritmo goloso è quindi del tutto assente l’idea di eseguire tentativi, ossia di eseguire scelte che potrebbero successivamente essere revocate sulla base di una verifica a posteriori delle loro conseguenze. Da qui la conseguenza che non tutti gli algoritmi sono corretti, cioè individuano la risposta del problema per ogni istanza di esso. Effettuare ad ogni stadio la scelta migliore sulla base delle informazioni disponibili a quello stadio non garantisce che alla fine del procedimento la soluzione trovata sia ottima. Può infatti accadere che la scelta ad uno stadio escluda, in stadi successivi, la possibilità di effettuare scelte che sarebbero cruciali per ottenere l’ottimo complessivo. Uno degli aspetti critici dell’uso della tecnica golosa è appunto dimostrare l’ottimalità della soluzione. La tecnica golosa è utilizzabile anche quando, pur non riuscendo a determinare l’ottimo di un problema, il suo calcolo è estremamente oneroso per cui la soluzione fornita dalla tecnica golosa, che ha tempi di esecuzione polinomiali, può costruire una buona approssimazione dell’ottimo; in questo caso è importante stabilire di quanto la soluzione golosa può discostarsi da quella ottima.
I problemi affrontati dalla tecnica golosa devono, per garantire la soluzione ottima, avere due proprietà fondamentali: la proprietà della scelta golosa e la proprietà dalla sottostruttura ottima.
1) Il problema P gode della proprietà della scelta golosa se, per ogni istanza i di P, è possibile calcolare una soluzione ottimale per i a partire dalla scelta golosa effettuata secondo il criterio di preferenza. In altre parole, la scelta golosa effettuata secondo il criterio di preferenza è sempre in grado di individuare una componete di una soluzione ottimale della istanza.
2) Il problema P gode della proprietà della sottostruttura ottima se, per ogni istanza i, una soluzione ottimale può essere calcolata combinando la scelta del 1° stadio con una soluzione ottimale ottenuta per una nuova istanza del problema P, i cui dati di ingresso hanno dimensione inferiore rispetto all’istanza i. In altre parole, la soluzione ottimale per i contiene in qualche modo la soluzione ottimale di sotto-istanze di i.
Anche la tecnica golosa, come quella di Backtracking, può essere rappresentata con un albero di ricerca. Mentre la tecnica di Backtracking si basa sull’idea di visitare l’albero di ricerca in profondità, un algoritmo goloso si può vedere come un procedimento che passa dalla radice ad una foglia seguendo un unico cammino cioè il nodo figlio che rappresenta l’elemento preferito da assegnare alla i-esima componete della soluzione.
La complessità asintotica di un algoritmo goloso è data da:
GOLOSO(n)= CINIZ (n)+CPREP(n)+nstd(n)*CSCELTA(n)
dove:
· CINIZ(n) è il costo delle operazioni di inizializzazione…
· CPREP(n) è il costo della preparazione dell’output….
· nstd(n) è il numero massimo di stadi previsti per la costruzione di un elemento dello spazio di ricerca.
· CSCELTA(n) è il costo delle operazioni che devono essere condotte in ogni stadio, compresa la scelta golosa.
4. LA TECNICA DIVIDE ET IMPERA consiste nel risolvere un problema mediante un’accorta suddivisione di esso in vari sottoproblemi. Più precisamente, si individuano k problemi aventi dimensioni più piccole, si risolvono ricorsivamente i k sottoproblemi individuati e si utilizzano le loro soluzioni per determinare quella del problema originale; la ricorsione si interrompe quando un sottoproblema raggiunge una dimensione tale da poter essere risolto direttamente.
L’algoritmo tipico è il seguente:
Tsoluzione DivideEtImpera ( const Tproblema& p)
{ if (p.dimensione<=dimmi)
return risolviDirettamente(p);
else
{ card k= individuaNumeroSottoProblemi(p)
Vettore<Tproblema> P(k);
P = individuasottoproblemi(p,k)
For (card i=1; i<=k; i++)
S[i]= DividiEtImpera (P[i]);
Return CombinaSoluzioni(S);}
}
Per applicare la tecnica è necessario disporre dei seguenti elementi:
· Una relazione di ordinamento sulle istanze del problema, tipicamente basata sulla dimensione dell’input, che disciplina l’induzione.
· Un metodo di risoluzione diretto per tutte le istanze del problema che non superano una determinata dimensione limite; tale metodo è relativo al passo base dell’induzione;
· Un meccanismo per suddividere i dati di ingresso relativi ad una istanza in diverse parti, ciascuna di dimensione minore di quella originaria, e rappresentante l’input di una nuova istanza della stesso problema.
· Un meccanismo per comporre le soluzioni per le istanze individuate dalla suddivisione del punto precedente per ottenere la soluzione per l’istanza originaria.
Lo schema dell’algoritmo si può quindi sintetizzare nel seguente modo:
1. se l’input ha dimensione inferiore ad un certo valore k, allora utilizza uno specifico metodo diretto per ottenere il risultato;
2. altrimenti, dividi l’input in parti, ciascuna di dimensione inferiore all’input originario (divide)
3. esegui ricorsivamente l’algoritmo su ciascuno degli input individuati al passo precedente;
4. componi i risultati ottenuti al passo precedente ottenendo il risultato per l’istanza originaria (impera);

Per quanto riguarda la complessità asintotica abbiamo che:
![]()
dove
a= al numero di sottoproblemi
bnd=al costo delle operazioni per suddividere l’input e ricombinare le risposte ottenute
d=0 se la ricomposizione viene eseguita in tempo costente, 1 se in tempo lineare, 2 ecc..
c= numero intero per il quale si suddivide il problema
n/c= dimensione del sottoproblema
Tabella riassuntiva di alcuni casi generici:
Caso d=0 a=1 T(n)= o(logn) esempio ricerca binaria
Caso d=1 a<c T(n)= o(n) esempio k-mo maggiore nel caso migliore
Caso d=1 a=c T(n)= o(nlogn) esempio mergesort
Caso d=1 a>c T(n)= o(nlogca) esempio moltiplicazione di interi con n cifre
5.LA TECNICA DI PROGRAMMAZIONE DINAMICA è una tecnica di realizzazione di algoritmi che risolvono un problema utilizzando le soluzioni di sottoproblemi. La differenza con la tecnica divide et impera è che divide et impera intende preliminarmente individuare solo quei sottoproblemi che sono rilevanti per la risoluzione del problema originario (metodo top-down) mentre la programmazione dinamica parte direttamente da tutti i sottoproblemi più piccoli per poi arrivare alla soluzione del problema originario (metodo bottom-up). L’algoritmo tipico della programmazione dinamica è iterativo.
Nel caso di un problema in cui solo un numero limitato di sottoproblemi è rilevante per determinare la soluzione finale, la tecnica divide et impera risulta più conveniente in quanto l’extra-lavoro per individuare i sottoproblemi è ripagato dal minor numero di sottoproblemi da risolvere. D’altra parte, se tutti o quasi tutti i sottoproblemi devono essere comunque risolti e, addirittura, accade che la soluzione di uno stesso sottoproblema debba essere usata più volte, allora la programmazione dinamica risulta essere la tecnica più conveniente poiché essa parte direttamente dalla soluzione di tutti i problemi di dimensione atomica per ricomporre via via le soluzioni di tutti i sottoproblemi di dimensione maggiori, risolvendo ogni sottoproblema solo una volta e conservando la sua soluzione in una tabella.
Un esempio di problema risolvibile con questa tecnica è quello della DISTANZA MINIMA TRA TUTTI I NODI DI UN GRAFO. Supponiamo che i pesi rappresentano le distanze tra i nodi incidenti. Questo problema può essere risolto applicando all’algoritmo di Dijkstra (che si basa sulla tecnica golosa) ad ogni nodo del grafo. Siccome la complessità dell’algoritmo di Dijkstra è Q(n2) e va applicato a n nodi la complessità arriva a Q(n3). Con la programmazione dinamica non si migliora in termini di efficienza ma il problema può essere risolto in maniera elegante e semplice. Inoltre, a differenza della tecnica golosa, esso è corretto anche in presenza di distanze negative (naturalmente a patto che non ci siano cicli negativi).
Indichiamo con d(i,j) il peso dell’arco da i a j; inoltre, dk(i,j), con 0£ k £ n, indica la distanza minima dei cammini da i a j in cui tutti i nodi intermedi s sono tali che s £ k. Pertanto d0(i,j) = d(i,j) e dn(i,j) è la distanza minima da i a j poiche praticamente non ci sono restrizioni sui nodi intermedi.
Il problema si risolve con la programmazione dinamica nel seguente modo:
Si pone all’inizio
d0(i,j) = d(i,j) per 1£ i £ n e 1£ j £ n e i¹j, e d0(i,i) = 0.
Quindi si calcolano le distanze dk(i,j) come:
dk(i,j) = min (dk-1(i,j), dk-1(i,k) + dk-1(k,j) "i : 1£ i £ n e "j : 1£ j £ n
La distanza minima da i a j con nodi intermedi con indice non superiore a k è diversa dalla distanza minima da i a j con nodi intermedi con indice non superiore a k-1 solo se esiste un cammino che abbia almeno un nodo intermedio con indice superiore a k-1 ma non superiore a k. Poiché non esistono cicli negativi, l'eventuale cammino migliore ha un unico nodo intermedio k e i sotto-cammini da i a k e da k a j non contengono a loro volta il nodo k come nodo intermedio e tutti i loro nodi intermedi hanno indice inferiore a k, per cui la loro distanza è già stata calcolata. Quindi vale il principio dell'ottimalità e dn(i,j) = d(i,j) per 1 £ i £ n 1 £ j £ n, forniscono le distanze minime tra ogni coppia di nodi.