di Massimo Fantin Novembre 2002

Home

Elementi teorici

Urto centrale

Urto obliquo

Urto contro la parete

Uso del programma di simulazione

Esempi

 Simulazione

L'urto tra due palline si dice elastico se vengono conservate sia la quantità di moto che l'energia cinetica.

Per studiare un urto elastico iniziamo dal caso dall'urto unidimensionale tra due corpi di masse m₁,m₂ aventi velocità iniziali v₁,v₂. Dopo l'urto le loro velocità saranno V₁, V₂. Le due equazioni delle leggi di conservazione citate si scrivono:

m₁ v₁ + m₂ v₂ = m₁ V₁ + m₂ V₂

1/2 m₁ v₁² + 1/2 m₂ v₂² = 1/2 m₁ V₁² +1/2 m₂ V₂²

che costituiscono un sistema nelle incognite V₁ V₂ la cui soluzione è ( tolta la soluzione banale V₁=v₁ , V₂ =v₂)

V₁ = (m₁ v₁ +2 m₂ v₂ - m₂v₁) / (m₁+m₂)

V₂ = (m₂ v₂ + 2 m₁ v₁ - m₁ v₂) / (m₁+m₂ )

Da questi risultati numerici possiamo considerare alcuni casi particolari:

V₁ = v₂

V₂ = v₁

Che sta a significare che nell'urto centrale tra due palline uguali, l'unico modo affinché si conservino sia la quantità di moto che l'energia cinetica è che ciascuna pallini acquisti la velocità dell'altra.

Se v₂=0 cioè una delle due palline sia ferma.

V₁ = (m₁ - m₂) v₁ / (m₁+m₂)

V₂ = 2 m₁ v₁ / (m₁+m₂ )

Significa che se m1 > m2 cioè la massa della pallina urtante è maggiore della pallina urtata entrambe continueranno nella stessa direzione, se invece la massa della pallina urtata è maggiore di quella della pallina urtante m₁<m₂ la prima pallina rimbalzerà.

Se v₂=0 e m1 >> m2 se la massa della pallina urtante è molto maggiore della pallina urtata avremo che m₂ risulta trascurabile rispetto ad m₁ e pertanto le formule si semplificheranno :

V₁ = v₁

V₂ = 2 v₁

Che significa che la pallina urtante proseguirà indisturbata mentre l'altra verrà lanciata con velocità doppia.

Se v₂=0 e m1 << m2 se la massa della pallina urtante è molto minore della pallina urtata avremo che m₁ risulta trascurabile rispetto ad m₂ e pertanto le formule si semplificheranno :

V₁ = -v₁

V₂ = 0

È il caso di una piccola pallina che rimbalza contro una molto più pesante.

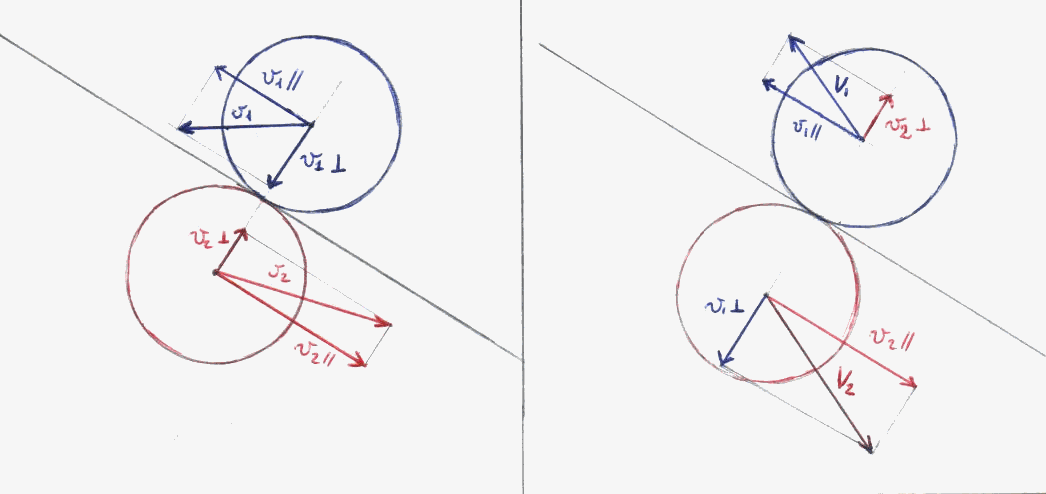
Se l'urto tra le due palline non è centrale nel senso che la direzione del centro della pallina urtante non è esattamente verso il centro della pallina urtante si parla di urto obliquo per studiarlo consideriamo inizialmente il caso in cui le due masse siano uguali e che l'urto avvenga come nella figura di sinistra nella quale sono rappresentate le velocità al momento dell'urto: v₁, v₂ scomponiamo le due velocità in direzione parallela al piano tangente ad entrambe le palline e in direzione perpendicolare e osserviamo che le componenti parallela al piano non vengono influenzate dall'urto pertanto rimarranno invariate mentre le componenti perpendicolari si comportano come nel caso dell'urto centrale pertanto, come osservato precedentemente nel caso m₁=m₂ si scambiano le velocità.

 Nella figura di sinistra sono rappresentate le velocità dopo l'urto dove le componenti perpendicolari al piano tangente sono scambiate.

Nel caso le due palline abbiano massa diversa nulla cambia per quanto riguarda le componenti parallele mentre quelle perpendicolari si trasformano secondo le equazioni generali studiate precedentemente per gli urti centrali.

Nel caso di un urto contro una parete si decompone la velocità in direzione parallela e perpendicolare alla parete, la componente parallela rimane invariata mentre quella perpendicolare viene orientata in verso opposto perché può esser pensato come un urto contro un altro corpo di massa enormemente maggiore, caso studiato precedentemente m₁<<m₂

Oggetti presenti nel piano della simulazione:

• Due palline in movimento di colore diverso: Il movimento della pallina viene seguito da una serie di cerchi dello che indicano la posizione ogni decimo di secondo. I l numero dei cerchi si può modificare o annullare.
• Due pannelli ( uno per ciascuna pallina ) per leggere e introdurre i dati. Ciascun pannello può essere spostato trascinandolo per il punto in alto a sinistra. I dati che possono essere letti sono:
• La massa della pallina e di conseguenza anche il suo diametro ( Il volume è circa proporzionale alla massa),: per modificare il valore della massa è sufficiente fare clic con il mouse sul + o sul -. La massa è espressa in kg.
• La posizione delle palline: per modificarla, da fermo trascinare la pallina con il mouse. La posizione è espressa in metri.
• La velocità: per azzerare la velocità fare clic su v=0 mentre per modificarla spostare, (quando è fermo) con il mouse l'estremo della molla, i valore si leggono sul pannello. Le velocità sono espresse in m/sec.
• Il numero dei cerchi di posizione
• Un pannello per il cronometro: Facendo clic sul cronometro il moto si ferma mentre ricliccando riparte( se non sono state operate modifiche, da dove è stato fermato, con la parte inferiore del pannello si può modificare l'accelerazione di gravità. Le velocità possono essere lette sui pannelli o dedotte dalle posizioni dei cerchi. I tempi sono espressi in secondi.
• Due regoli: uno orizzontale e l'altro verticale per poter misurare delle distanze. I regoli si possono spostare trascinandoli dall'origine. Le misure dei regoli sono in metri.

Urto centrale: Per simulare un urto centrale azzerare la gravità g = 0. Posizionare le due palline esattamente alla stessa altezza ( posizionarle con attenzione in modo che le seconde coordinate della posizione siano uguali) , e le velocità orizzontale ovvero con la seconda componente della velocità sia nulla. Si assegnano i valori delle masse e si dà il via . Si osservano le velocità prima e dopo gli urti facendo tutte le considerazioni dal caso ( conservazione della quantità di moto, dell'energia ).

 Caduta dei gravi: Per studiare la caduta da una certa altezza, scegliere un valore dell'accelerazione di gravità ( g =10 ), posizionare il righello verticale in modo che in corrispondenza del pavimento sia segnata l'altezza dalla quale si vuole far cadere la pallina, diminuire al minimo la massa della pallina in modo da poter lavorare con un oggetto piccolo, posizionare la pallina in modo che la parte inferiore di essa appoggi sullo zero del righello, azzerare le velocità con il tasto v = 0 e avviare il cronometro, attendere che la pallina cada e ritorni al punto di partenza e fermare il cronometro, ripetere diverse volte l'esperienza, fare la media delle misure ottenute e verificare se il tempo di caduta corrisponde a quello calcolabile

T= Ö ( 2 h/g).

Si possono, in modo analogo studiare anche il moto di un grave con velocità iniziale non nulla: problema balistico.

Interazione tra due palline in caduta Si possono far cadere due palline sulla stessa verticale al fine di studiare lo scambio di energia e verificare che la conservazione dell'energia totale. Si posizionano le due palline sulla stessa linea verticale ( in modo che abbiano esattamente la stessa coordinata x , altrimenti le palline scappano lateralmente e non si riesce più a osservare il fenomeno ) , si differenziano le masse ( non troppo ), si annullano le velocità e naturalmente si dà un valore non nullo a g. Si lasciano cadere la palline e si osserva che le due palline si scambiano energia cinetica e potenziale. Per verificare la conservazione dell'energia si può fermare il sistema più volte e verificare che la somma delle due energie cinetiche e delle due energie potenziali è costante ed è uguale al valore delle energia potenziale iniziale.

Urto obliquo per studiare l'urto obliquo si annulla l'accelerazione di gravità g=0, si posizionano le palline in modo da poterne lanciare una contro l'altra ferma in un urto obliquo, si annulla la velocità della palline che verrà urtata e si dà il via, scegliendo anche un opportuno numero di tracce. Si osserverà che dopo l'urto le due palline partono in direzione perpendicolari tra loro e che la somma delle quantità di moto prima dell'urto e dopo rimane costante, Per misurare le quantità di moto si possono leggere le velocità sui pannelli delle palline o anche misurando lo spazio tra un cerchio e l'altro.