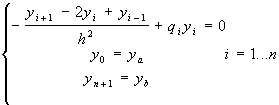
Stati stazionari in una buca di potenziale
di Massimo Fantin
Novembre 2000
Se pensiamo ad una corda di chitarra in vibrazione ci rendiamo conto che essa può vibrare emettendo, oltre alla fondamentale solo le armoniche multiple di essa, le altre frequenze non sono ammesse perché, la velocità di propagazione sulla corda è costante e le onde devono giungere agli estremi sempre nella posizione nulla, perché sono tenute fisse dal ponticello.
Questo problema può essere risolto matematicamente risolvendo l'equazione del tipo:
-y''- w 2 y =0 con le condizioni al contorno: y(a)=0, y(b)=0.
Osserviamo che si tratta di una equazione semplificata perché la variabile tempo è stata eliminata. La y rappresenta lo spostamento massimo della corda.
Risolviamo l'equazione ponendo b = 2 p .
Le soluzioni sono del tipo: y = A sin (w x + j ), introducendo le condizioni al contorno le soluzioni accettabili sono:
la soluzione identicamente nulla che si attiene per qualsiasi valore di w mentre per i valori seminteri di w si anno le soluzioni:
y = A sin w x
che sono le soluzioni stabili e corrispondono alle vibrazioni della corda corrispondenti alle frequenze della fondamentale e delle armoniche.
Un problema analogo dal punto di vista matematico ma diverso per la sua natura si presenta in fisica quantistica nel moto di una particella in una buca di potenziale rettangolare con pareti infinitamente alte
Ci proponiamo ora di usare il metodo numerico per risolvere un problema un po' più generale:
-y''+q(x) y=0 con le condizioni al contorno y(a)=ya y(b)=yb.
Applichiamo ora il metodo delle differenze che consiste nel suddividere l'intervallo [a,b] con n+1 punti xi equidistanti e tali che x0 = a xn+1 = b mentre qi =q(xi).
Si sostituiscono le derivate con i rapporti incrementali: in particolare:
y'' viene sostituito da ( y(x+h)-2 y(x)+y(x-h)) / h2
Si eliminano i termini di ordine superiore e l'equazione si riduce alla risoluzione del sistema in n equazioni ed n incognite y1,y2...yn
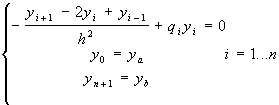
che può essere scritto:

La matrice completa del sistema è:
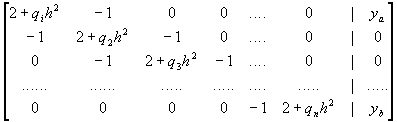
Questo sistema può essere facilmente risolto ponendo ci l'elemento i-esimo della diagonale principale triangolando la matrice ponendo dalla seconda riga in poi ci = ci /ci-1 e yi = yi - yi-1 / ci-1 dove yi è l'elemento i-esimo della colonna dei termini noti.
Si ottiene:
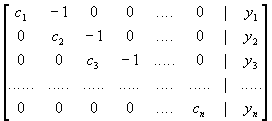
Le soluzioni si ottengono facilmente:
xn = yn / cn
..............
xi =(yi + xi+1)/ci
..............
il tutto si può fare utilizzando solo tre vettori: c,y,v e non tutta la matrice rendendo la cosa molto più veloce.
Se applichiamo questo metodo al problema delle corde vibrante ponendo y(0)=y(2p )=0 otteniamo la soluzione nulla che non è interessante. Per ottenere delle soluzioni non banali occorre, come per le corde della chitarra, pizzicarle cioè introdurre al sistema una piccola perturbazione ponendo per esempio y(2p ) leggermente diversa da zero. Si scopre così che solo i valori di w 2=q(x)=n2 con n semintero danno luogo a vibrazioni significative mentre per gli altri valori si ottiene solo la soluzione nulla. Si osserva che aumentando il numero delle suddivisioni è possibile aumentare notevolmente la selettività delle frequenze di risonanza, cioè se il valore di w 2 differisce di poco dalla soluzione non si discosta da quella nulla..
Affrontiamo ora il secondo problema di fisica quantistica. Ad ogni particella viene associata un'onda la cui equazione di Schrodinger semplificata dalla variabile tempo può essere scritta in modo analogo:
-h/2p m F ''(x) +(E-V(x))F(x) =0.
A parte la costante numerica, se V(x) è costante si ottiene l'equazione già studiata e le soluzioni già studiate vengono interpretate come gli stati stazionari della particella nella buca di potenziale. Si osserva che solo per alcuni valori discreti di energia esistono soluzioni stabili.
Bohr riuscì a spiegare le righe dello spettro di emissione dell'atomo di idrogeno ipotizzando l'esistenza di solo alcune orbite stabili, egli avanzò ipotesi semiclassiche che diedero risultati compatibili con quelli sperimentali. Successivamente, grazie allo sviluppo della meccanica quantistica l'ipotesi di Bohr è diventata una conseguenza naturale dell'equazione di Schrodinger che, risolta nel caso dell'atomo di idrogeno consentiva di vedere le orbite dell'elettrone come delle zone nelle quali la probabilità di trovare un elettrone è molto più alta che altrove.
Una cosa analoga si può vedere nell'esempio seguente nel quale l'algoritmo precedentemente studiato ci consente di risolvere il problema anche quando V non è costante, cosa che sarebbe molto difficile da studiare analiticamente.
Secondo l'interpertazione data del significato della funzione F che è una funzione a valori complessi, si pensa che il suo quadrato rappresenti la probabilità di trovare la particella in quel dato punto. Per trovare l'analogo classico della funzione di probabilità si può pensare che da E-V=1/2 m v2 si risolva in v e se ne calcoli l'inverso. Si ha:
![]()
Questa funzione è proporzionale alla probabilità di trovare la particella infatti maggiore è la velocità minore sarà il tempo in cui la particella permane in un elemento dx
Per calcolare la probabilità dividerla per l'integrale della stessa funzione calcolato su tutti i valori che può assumere.
Si può notare che all'aumentare dell'energia E della particella i valori di probabilità dati dalla meccanica quantistica si avvicinano a quelli indicati dalla meccanica classica.
Bibliografia
La fisica di Berkeley Fisica quantistica Zanichelli
Josef Stoer Introduzione all'analisi numerica Zanichelli.
Esempio 1 Buca rettangolare
Se si immagina di far vibrare la particella in una buca rettangolare con pareti infinitamente alte si trova che sono possibili solo quelle oscillazioni sinusoidali di lunghezza d'onda l = l / 2 n e che corrispondono ai valori di energia proporzionali ai quadrati dei numeri interi,
Se invece costruiamo una buca rettangolare con le pareti maggiori dell'energia della particella ma non infinita, ci accorgiamo che l'onda si propaga anche al di là della buca col significato che esiste una certa probabilità di trovare la particella anche in zone nelle quali l'energia potenziale è superiore a quella potenziale.
Esempio2 Pendolo quantistico
Si immagina di far vibrare una particella di energia E in una buca di potenziale a forma sinusoidale.
Lo chiamiamo 'pendolo' perché anche l'analogo classico possiede una energia potenziale dipendente sinusoidalmente dall'ampiezza.
Si determinano sperimentalmente alcuni stati stazionari e si interpreta il quadrato della funzione d'onda |F (x)|2 come la probabilità di trovare la particella nella posizione x, si ottiene la distribuzione che può essere confrontata con quella classica .
Per trovare la probabilità classica si pensa che la densità di probabilità dP sia inversamente proporzionale alla velocità:
Se q = E sin w t si ha:
![]()
Per ottenere la distribuzione delle probabilità occorre moltiplicare per una costante in modo che l'area complessiva sia unitaria, ma visto che
![]()
si ha nel nostro caso
![]()
che è rappresentabile e dove si nota che all'aumentare dell'energia del pendolo, cioè al passare dalla microfisica alla fisica ordinaria la soluzione quantistica si avvicina a quella classica infatti la curva della distribuzione classica sembra muoversi lungo la media di quella quantistica.
Esempio 3 Effetto Tunnel dovuto ad un ostacolo rettangolare.
Se all'interno della buca è presente un ostacolo di altezza maggiore dell'energia della particella, secondo la meccanica classica la particella si deve trovare o da una parte o dall'altra dell'ostacolo mentre per la fisica quantistica, se l'ostacolo è sottile, esiste una certa probabilità che la particella possa attraversare l'ostacolo e trovarsi nell'altra zona, esistono stati stazionari nei quali è più probabile che la particella si trovi da una parte dell'ostacolo che dall'altra ma comunque esiste sempre la possibilità di saltarlo.
Esempio 4 Rampa
Se la buca ha la forma di una rampa : è, in parte costante e per il resto inclinata, si può notare come la forma dell'onda si mantiene costante nella parte in cui il potenziale è costante mentre nella zona in salita l'onda rallenta la sua velocità infatti è proporzionale alla differenza tra E-V. Si nota dai grafici che la probabilità di trovare la particella sia dal punto di vista classico che relativistico aumenta all'aumentare dell'altezza.
Uso del programma di simulazione
Mediante questo applet è possibile osservare il comportamento di una particella in una buca di potenziale secondo l'equazione di Schrodinger. È possibile scegliere diversi forme per la buca : buca rettangolare, sinusoidale (pendolo quantistico), o a rampa. è possibile inoltre osservare l'effetto tunnel interponendo un ostacolo rettangolare, la scelta si effettua mediante la finestrella a sinistra.
Significato dei grafici
![]() Il grafico blu rappresenta il potenziale ( la profondità della buca),
Il grafico blu rappresenta il potenziale ( la profondità della buca),
![]() Il grafico verde il livello dell'energia della particella E.
Il grafico verde il livello dell'energia della particella E.
![]() Il grafico nero in movimento rappresenta istante per istante l'andamento della funzione d'onda F (x)
Il grafico nero in movimento rappresenta istante per istante l'andamento della funzione d'onda F (x)
![]() Il grafico rosa rappresenta il quadrato della funzione d'onda (F (x))2 che, secondo l'interpretazione statistica che viene data sta ad indicare la probabilità che ha la particella di trovarsi in qual dato punto.
Il grafico rosa rappresenta il quadrato della funzione d'onda (F (x))2 che, secondo l'interpretazione statistica che viene data sta ad indicare la probabilità che ha la particella di trovarsi in qual dato punto.
![]() Il grafico azzurro rappresenta la probabilità che ha la p0articella di trovarsi in quel dato punto secondo la meccanica classica.
Il grafico azzurro rappresenta la probabilità che ha la p0articella di trovarsi in quel dato punto secondo la meccanica classica.
Significato dei tasti in basso :
Gli zoom servono per modificare la finestra grafica.
I tasti volume aumentano o diminuiscono l'ampiezza delle oscillazioni ed hanno come unico scopo quello di rendere il fenomeno meglio visibile.
Trascinamenti realizzabili con il mouse:
![]() Spostamento in alto e in basso della linea verde dell'energia, nel momento in cui si lascia il mouse automaticamente il livello energetico si posiziona nello stato stazionario più vicino ovvero quel valori di energia che consente una vibrazione di massima ampiezza..
Spostamento in alto e in basso della linea verde dell'energia, nel momento in cui si lascia il mouse automaticamente il livello energetico si posiziona nello stato stazionario più vicino ovvero quel valori di energia che consente una vibrazione di massima ampiezza..
![]() Spostamento a destra o a sinistra delle due fasce blu laterali, trascinare sul confine interno. Queste fasce delimitano inderogabilmente la buca di potenziale, in esse il potenziale è infinitamente alto pertanto al f8unzione d'onda è zero.
Spostamento a destra o a sinistra delle due fasce blu laterali, trascinare sul confine interno. Queste fasce delimitano inderogabilmente la buca di potenziale, in esse il potenziale è infinitamente alto pertanto al f8unzione d'onda è zero.
![]() Spostamento e modifica delle buche, in particolare:
Spostamento e modifica delle buche, in particolare:
![]() Nella buca rettangolare e nell'ostacolo rettangolare si può trascinare l'altezza.
Nella buca rettangolare e nell'ostacolo rettangolare si può trascinare l'altezza.
![]() Nella buca sinusoidale è possibile trascinare l'altezza estrema, dove è costante il valore del potenziale. Trascinando il livello costante al di sotto del livello zero si possono studiare interessanti casi di effetto tunnel.
Nella buca sinusoidale è possibile trascinare l'altezza estrema, dove è costante il valore del potenziale. Trascinando il livello costante al di sotto del livello zero si possono studiare interessanti casi di effetto tunnel.
![]() Nella rampa si può trascinare la parte obliqua
Nella rampa si può trascinare la parte obliqua