Funzioni particolari della matematica e della fisica
Massimo Fantin
Distribuzione degli errori di Gauss
Funzioni di Bessel di ordine intero
Distribuzione delle velocità delle particelle di un gas di Maxwell
Spettro di emissione di Corpo nero di Plank
Programma per la rappresentazione
La Funzione degli errori di Gauss
La Distribuzione normale o gaussiana ha equazione
![]()
dove m è il valor medio della distribuzione e s è lo scarto quadratico medio
Nella rappresentazione è possibile scegliere i valori di M e di s trascinando il grafico dalle linee verticali che rappresentano tali valori.
E possibile inoltre calcolare il valore dell'integrale tra due valori assegnati e il valore della funzione in un punto assegnato
La funzione Gamma è una funzione continua definita per orni valore di R tranne per i valori interi negativi dove presenta asintoti verticali.
![]()
Generalizza il fattoriale nel senso che per valori naturali G (n) = (n-1)!
Per il calcolo numerico dei valori della funzione gamma si usa la seguente approssimazione che è sufficientemente buona per valori maggiori di 5,
![]()
per gli altri valori si utilizza la proprietà: G (n) = G (n+1)/(n+1) che è la stessa proprietà caratteristica del fattoriale e che può essere anche facilmente dedotta dalla definizione data sopra integrando per parti.
Le funzioni di Bessel di ordine intero
Sono le soluzioni dell'equazione differenziale
![]()
e sono date dalla somma della serie:
![]()
che definisce la funzione di Bessel di ordine n
Distribuzione delle velocità delle particelle di un gas perfetto di Maxwell
![]()
N(v) dv rappresenta il numero totale delle particelle di velocità compresa tra v e v+dv, m rappresenta la massa delle particelle, N il numero totale delle particelle del gas, k la costante di Boltzmann, T la temperatura assoluta.
Nella rappresentazione della distribuzione è possibile variare la temperatura T modificando il grafico e calcolare l'integrale tra due valori assegnati al fine di calcolare il numero delle particelle aventi velocità comprese tra due valori assegnati.
Spettro di emissione del corpo nero di Plank
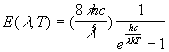
dove E(l ,T) è la densità di energia raggiante, l è la lunghezza d'onda, T è la temperatura assoluta, k la costante di Boltzmann e h è la costante di Plank.
Si può determinare per un determinato valore di T il valore di l per cui è massima l'energia irradiata:
l
max=0.2014 h c / (T k).Nella rappresentazione grafica è possibile modificare la temperatura del corpo nero e verificare come cambia lo spettro di emissione, in particolare è possibile osservare a quale valore deve arrivare la temperatura affinché inizi ad emettere luce visibile. Lo spettro della luce visibile è indicato nel grafico.