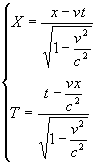ponendo c=1 e v=3/5 si ha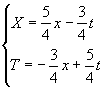 
L’esempio
seguente ha lo scopo di mostrare che la simultaneità di due eventi dipende dal
sistema di riferimento rispetto al quale consideriamo gli eventi. Due eventi
simultanei rispetto ad un sistema di riferimento non lo sono rispetto ad un
altro in moto rettilineo rispetto al primo.
Un
treno relativistico lungo 2 secondi-luce sfreccia alla velocità di 3/5 della
velocità della luce, sulla linea
ferroviaria è posizionato un petardo che esplode esattamente nell’istante in
cui su di esso passa il centro del treno. Dall’esplosione vengono emessi
due lampi: uno nella direzione della testa del treno e l’altro nella
direzione della coda. Per
l’osservatore esterno ovviamente il lampo di coda giunge prima del lampo di
testa in quanto la coda del treno si avvicina al punto centrale da cui è stato
emesso mentre la testa si allontana.
Per
calcolare le coordinate spazio temporali degli eventi di A e B nei quali i lampi
giungono rispettivamente in testa e in coda, scriviamo le equazioni del moto
della testa e della coda del treno e le mettiamo a sistema con l’equazione
dei lampi di luce ( la velocità della luce è considerata unitaria come
pure il secondo luce.)
A(
x = t , x = 1+3/5 t) che
risolvendolo si ottiene A=(5/2,5/2)
B(
x =-t, x = -1è3/5 t) che risolvendo si ottiene
B=(-5/8,5/8)
Gli
eventi A e B sono rappresentati in blu nel grafico.
Evidentemente
i due eventi non sono contemporanei come si è gia detto.
Applichiamo ora le trasformazioni di Lorentz per
calcolare le corrispondenti coordinate spazio-temporali degli stessi eventi
rispetto però al sistema di riferimento del treno:
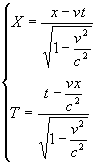ponendo c=1 e v=3/5 si ha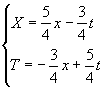
I trasformati sono:
Che sono rappresentati in rosso nel grafico.
Osservazioni: 1) Mentre gli eventi A e B visti dal sistema di riferimento della ferrovia, esterno al treno, non sono simultanei, gli stessi eventi considerati rispetto al sistema di riferimento del treno sono invece simultanei ovvero i lampi di luce giungono nello stesso istante agli estremi del treno.
2) Osserviamo inoltre che, anche la lunghezza del treno è relativa al sistema di riferimento infatti per il riferimento esterno la lunghezza è, come si è detto di due unità, mentre per il riferimento interno è di 5/2 unità, si calcola dalla differenza delle coordinate temporali degli eventi A’ e B’. Questo fenomeno è noto come contrazione delle lunghezze nel senso che la lunghezza del treno è maggiore se lo misuriamo sul treno in movimento che se lo misuriamo a terra. Spesso erroneamente si pensa che se il treno ci sfreccia davanti la lunghezza del treno diminuisca. Non è esatto, infatti se la misura la facciamo dall’esterno del treno non vediamo alcuna contrazione, la contrazione si ha quando si passa dalla misura fatta dall’interno a quella fatta all’esterno.
3) Osserviamo inoltre dal grafico anche il fenomeno della dilatazione del tempo, se calcoliamo il tempo che, secondo il sistema di riferimento esterno occorre affinché il centro del treno diventi l’evento medio ( graficamente il punto medio) degli eventi A e B di ricezione dei lampi di luce, otteniamo C(15/16, 25/16). Il tempo è 25 /16 mentre rispetto al sistema di riferimento del treno il tempo trascorso è soltanto 5/4. Se noi guardassimo dall’esterno, tenendo conto naturalmente del tempo che impiega la luce per giungere a noi, vedremmo l’orologio del treno andare più lentamente del nostro, mentre nel nostro passano 25/16 , nel loro passano solo 20/16.
