Di Massimo Fantin 2008
Per radicale doppio cubico reale intendiamo un radicale del tipo
Come per i radicali doppi quadratici, in alcuni casi è possibile ridurli.
Affinché sia riducibile bisogna che il radicando sia il cubo di un binomio radicale cioè deve essere del tipo:
pertanto
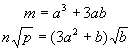
poiché la
parte radicale di
non è univocamente
determinata, ( essendo possibile portare dentro al segno di radicale i fattori
di n), per poter affermare che le due parti irrazionali coincidano cioè che b =
p bisogna esaminare le varie
rappresentazioni del suddetto radicale e vedere se ce ne è una per cui
(n-p)/3 è un quadrato perfetto, in tal caso si pone
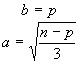
e, considerato che a può assumere valori opposti, si verifica se
in tal caso il radicale è riducibile e precisamente
Esempio 1,
Per calcolare il radicale doppio cubico
si osserva che (29-2)/3 = 9 che è il quadrato di 3, supponendo che a = 3 e b = 2 si verifica che
pertanto
Esempio 2,
Per calcolare il radicale doppio
si osserva innanzitutto che (174-3)/3=57 non è un quadrato perfetto, si scompone in fattori 174 ottenendo 2*3*29 e di conseguenza
per ciascun radicale verifichiamo se (n-p)/3 è un quadrato perfetto.
Si ha che (87-12)/3=25 ,poniamo quindi b=5 e a=12, verifichiamo infine che
pertanto
E’ possibile risolvere anche radicali doppi complessi del tipo
dove i è l’unità immaginaria. Si procede in modo analogo al caso precedente sviluppando il cubo del binomio complesso radicale
si procede in modo analogo al precedente cercando tra le possibili rappresentazioni del radicale interno quella per cui (n + p)/3 è un quadrato perfetto e si pone
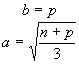
tenendo conto del fatto che a può assumere valori opposti si verifica se
Bisogna osservare che di radici cubiche di un numero complesso ce ne sono 3, calcolata la prima, le altre si trovano moltiplicandola per le radici cubiche dell’unità:
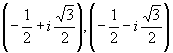
Esempio
Si osserva che (9+3)/3= 22 si pone b=3 e a=2. Si verifica che
pertanto
.
I valori che si ottengono moltiplicandola per le radici dell’unità sono:
