di Massimo Fantin
Simulazione java:
Vengono simulate le oscillazioni di due
pendoli coniugati ovvero lo stesso pendolo fatto oscillare intorno a due punti
distanti tra loro un metro.
Il pendolo è costituito da due masse M e m
rappresentate dai cerchi nero e blu. Le due masse possono essere
modificate cliccando i quattro tasti in alto a sinistra ( l'esperienza può
essere svolta anche mantenendo i valori iniziali) le masse possono essere
spostate trascinandole con il mouse. La massa M (nera), una volta scelta la
posizione deve essere lasciata ferma per tutta l'esperienza pertanto la
chiamiamo massa fissa. mentre spostando la massa blu,( massa mobile) si variano
i periodi di oscillazione. Spostando la massa blu si sposta contemporaneamente
la linea nera verticale in basso che taglia due grafici rosso e verde
corrispondente ai due pendoli, tali grafici rappresentano i tempi di
oscillazione al variare appunto della posizione del peso mobile.
IL punto azzurro su entrambi i pendoli
indica le posizioni del baricentro, che vengono anche
segnati in basso sulla scala tacchettata in decimi di lunghezza del pendolo, la
due tacche più lunghe indicano i punti di sospensione posti a un metro di
distanza.
In alto sono indicati i paramenti dei pendoli nelle unità del SI. :
x
indica la posizione pel peso blu del primo pendolo,
h la posizione del peso
fisso del primo pendolo,
m e M le masse e T il tempo.
Per fermare o far
ripartire il pendolo basta cliccare sullo sfondo giallo.
Osservando i grafici in basso si vede che si incontrano
in tre punti, ovvero esistono tre posizioni della massa mobile che rendono
uguali i periodi di oscillazione, di queste posizioni soltanto due possono
essere usate, non può essere usata la posizione che rende uguali i due
baricentri, mentre le altre due possono indifferentemente andare
bene.
Lo scopo del pendolo reversibile di Kater è
quello di misurare con grande precisione l'accelerazione di gravità, questo è
possibile per il fatto che possiamo misurare con la massima accuratezza la distanza
tra i due coltelli che costituiscono i punti di sospensione.
Per studiare il comportamento del pendolo reversibile partiamo dal pendolo fisico, pensato come in corpo rigido con un asse orizzontale fisso. Se l è la distanza tra l'asse e il baricentro G del corpo fisso e I il momento d'inerzia rispetto all'asse di rotazione si ha :
![]()
supponendo l'angolo q picco diventa sen q = q pertanto l'equazione diventa:
![]()
la cui soluzione è una funzione armonica di periodo
![]()
E' interessante a questo punto introdurre la lunghezza ridotta come la lunghezza del pendolo semplice di ugual periodo.
Si avrà
![]()
Se entrambi i pendoli hanno lo stesso periodo di oscillazione si avrà che le lunghezze ridotte sono uguali: pertanto l'equazione
![]()
che risolta rispetto a x fornisce le seguenti soluzioni:
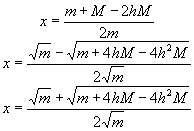
sostituendo tali valori di x nella equazione del periodo e semplificando si ottengono i seguenti valori
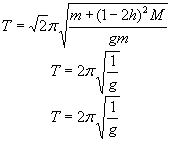
Da qui si vede che, esistono tre posizioni del peso mobile che producono lo stesso periodo di oscillazione però solo due di essi che danno lo stesso valore del pendolo semplice avente per lunghezza la distanza tra i due coltelli di sospensione, misura che può essere misurata con grande precisione. pertanto l'accelerazione di gravità si calcola con
![]()
Poiché è molto difficile misurare il periodo in un punto esatto nel quale avviene l'uguaglianza dei due periodi, si può procedere in questo modo:
si posizionano i pendoli in una posizione prossima e si prende nota dei due periodi di oscillazione che indichiamo con T11,T21, Si ripetono le stesse misure spostandoci leggermente ottenendo i tempi: T12, T22 A questo punto si procede con una interpolazione lineare, ovvero si calcolano le equazioni delle due rette interpolanti le due coppie di punti e si cerca il punto di intersezione, a conti fatti si trova la seguente formula facile da applicare
T = (T11*T22-T21*T12)/(T11+T22-T21-T12)
che permette di ottenere un ottimo valore per T da utilizzare nella formula precedente per il calcolo di g.