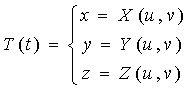
Di Massimo Fantin 2008
Una superficie nello spazio è localmente rappresentabile da una funzione continua del tipo:
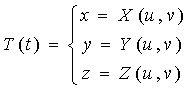
che rappresenta una mappa della superficie, cioè una funzione che da un dominio di R2 va in R3.
Se la mappa è sufficientemente regolare esiste la matrice delle derivate:
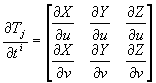
mediante le quali possiamo definire le componenti locali della metrica, che secondo la convenzione di Einstein di non scrivere la sommatoria per gli indici interni si scrive
![]()
che scritte per esteso diventano
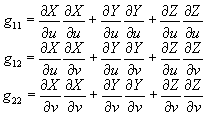
Queste componenti locali permettono di definire localmente la metrica ds che secondo le convenzioni di E si scrive
![]()
mentre per esteso:
![]()
che permette di calcolare sulla mappa la lunghezza di un percorso sulla superficie.
I coefficienti g permettono altresì di determinare la geodetica uscente da un punto e di data direzione. Prima di arrivare a questo si introduce il simbolo di Cristoffel
![]()
che permettono di fare lo spostamento parallelo di un vettore A lungo l’intervallo dx
![]()
La geodetica si ottiene spostando parallelamente a sé stesso un vettore in modo il trasportato sia ancora nella stessa direzione.
L’equazione della geodetica è
![]()
La geodetica è la curva per la quale è minima la distanza calcolata mediante le componenti locali da un punto e l’altro.