Presentazione

Questo ipertesto è nato dalla riflessione sul fatto che i gas sono costituiti da un gran numero di molecole in moto disordinato l’una rispetto all’altra, ogni molecola viene pensata come una pallina che si muove secondo le leggi della meccanica classica, urta contro altre molecole e contro le pareti del recipiente con urti elastici. Ho voluto costruire concretamente un modello di gas che fosse facile da osservare e che fosse possibile misurare le grandezze termodinamiche e verificare su di esso le leggi studiate teoricamente.

Il modello che viene presentato è leggermente diverso da quello che si studia in termodinamica classica infatti le molecole sono rappresentati da dischi (oggetti bidimensionali) e si muovono in una porzione di piano (un rettangolo). Mentre nella teoria cinetica classica le molecole si muovono in una porzione di spazio tridimensionale. Questa semplificazione fa si che le formule qui studiate differiscano da quelle classiche, come si vedrà nella trattazione teorica, in particolare: Il volume è, nel nostro modello una superficie tuttavia continueremo a indicalo con la lettera V.

L'aspetto interessante è che il programma tiene sotto controllo le grandezze microscopiche (velocità e posizione ) di tutte le molecole e le grandezze macroscopiche misurate (volume, pressione e temperatura ) dipendono dalle corrispondenti grandezze microscopiche. Questa particolare costruzione fa si che esista una certa instabilità nelle grandezze misurate, Il motivo sta nell'esiguo numero di molecole di cui è costituito il gas. Cento sono molto poche rispetto al numero di molecole di cui è costituito un gas reale, tuttavia è possibile effettuare delle misure significative.

Vista la instabilità delle grandezze termodinamiche è necessario effettuare molte misure e considerare le medie e gli scarti indicheranno le incertezze.

Per lo studio teorico si procede in modo analogo a come si fa nella teoria classica della cinetica dei gas.

Teoria cinetica

Il gas è formato da n molecole di massa m che si suppongono circolari, in moto casuale, si urtano fra di loro e urtano contro le pareti del recipiente, tre pareti sono fisse mentre una è mobile ( stantuffo).

Quando una molecola si scontra contro una parete fissa la componente della quantità di moto nella direzione normale alla superficie inverte di direzione mentre rimane invariata la componente nella direzione parallela alla superficie ( urto elastico contro una parete di massa infinita), questa variazione della quantità di moto si traduce in una forza e quindi in una pressione .

Per calcolare la pressione esercitata da ogni molecola di un gas contro le pareti del recipiente calcoliamo la forza come variazione della quantità di moto rispetto al tempo;

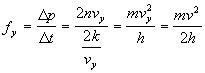
essendo supposto le velocità medie lungo le due direzioni siano uguali e che

dove l e h rappresentano l’altezza e la larghezza del contenitore, v la velocità e v_x, v_x le componenti della velocità lungo x e y.

La pressione esercitata da tutte le n molecole sarà pertanto:

dove U rappresentano l'energia interna e V il volume (la superficie).

La pressione si calcola anche come rapporto tra la forza peso dello stantuffo e la sua lunghezza:

dove M rappresenta la massa dello stantuffo, g l'accelerazione di gravità.

Da cui si ricava che l'equilibrio si raggiunge quando U= h M g.

La temperatura viene definita come l'energia cinetica media delle molecole

T=U / n.

L'equazione del gas perfetto, per quanto detto è pertanto:

P V = n T

 Si osserva quindi che il valore della costante di Boltzmann dei gas, nel nostro modello è uno, inoltre non si parla di moli ma di molecole pertanto non ha senso parlare della costante R.

Le unità di misura delle grandezze fisiche  sono arbitrarie,

Trasformazioni isobare e isoterme

Possiamo, analogamente a come si fa per i gas, considerare le trasformazioni Isotermiche, Isocore, isobare per le quali valgono le note leggi dei gas.

Anche i lavori compiuti durante le suddette trasformazioni assumono i soliti valori:

Trasformazione isobara

L = P (V2-V1)

Trasformazione isoterma

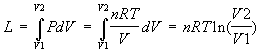
nel nostro modello:

L = n T ln ( V2/V1 )

Trasformazioni adiabatiche

Per calcolare il valore di gamma nel nostro modello procediamo analogamente a come si fa in termodinamica, calcoliamo le capicità termiche a volume costante e a pressione costante.

C_v = dQ/dT = dU/dT perché essendo una trasformazione a volume costante il lavoro è zero e dal primo principio segue che dQ=dU.

Ma essendo U=nT si avrà che c_v=d nT/dT=n.

C_p= dQ/dT= (dU+dL)/dT= n+ dL/dT= n+d PV/dT= n+d nT/dT=n+n=2n.

I calori specifici saranno riferiti a una molecola e varranno rispettivamente 1 e 2.

Pertanto il rapporto tra i calori specifici y = 2 e l'equazione della adiabatica nel nostro modello è

P V ² = P₀ V₀²

Il lavoro prodotto in una trasformazione adiabatica si calcola

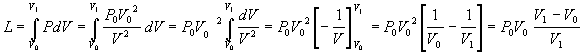
Se una molecola P1 con velocità v1 urta una molecola P2 con velocità  v2, per trovare le velocità dopo l'urto si consideri il piano (retta) tangente alle palline nel punto di contatto, le quantità di moto si scompongono nelle direzioni parallele e perpendicolare al piano, le componenti parallele vengono conservate dalle particelle mentre le componenti perpendicolari vengono scambiate. E' facile verificare che in questo modo si conservano sia la quantità di moto totale ( la somma delle quattro componenti rimane la stessa) che l'energia cinetica ( la somma dei quadrati delle quattro componenti rimane pure la stessa).

Urto contro lo stantuffo

 La particella di massa m che urta contro lo stantuffo di massa M conserva la componente orizzontale della quantità di moto mentre interferirà per quanto riguarda la componente verticale. Per la quale è possibile risolvere facilmente il problema applicando la conservazione della quantità di moto e dell'energia cinetica; posti v₁ e V₁ le velocità iniziali della particella e dello stantuffo e v₂ e V₂ le velocità dopo l'urto , risolvendo il sistema

  MV₁ + m v₁ = MV₂ + m v₂

 MV₁ ²+ m v₁ ²= MV₂ ²+ m v₂²

Si ottiene:

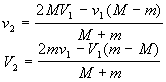
che esprimono le componenti verticali delle velocità dopo l'urto.

Dove V₁ Y₁ rappresentano la posizione e la velocità iniziale dello stantuffo mentre V₂ Y₂ quelle finali

E' facile verificare che anche queste ultime trasformazioni conservano l'energia totale dello stantuffo infatti la diminuzione di energia cinetica dovuta all'accelerazione di gravità viene immagazzinata sotto forma di energia potenziale.

In generale l'energia totale del sistema che si conserva nelle trasformazioni adiabatiche è data da:

E_Tot= U + 1/2Mv² + Mgh.

Nelle trasformazioni isobare in comportamento è simile con la sola differenza che in queste ultime si agisce sulla temperatura pressione mentre nelle prime sulla pressione.

Nelle trasformazioni isoterme rimane costante l'energia interna U pertanto se il gas si espande l'energia potenziale acquisita dallo stantuffo non si ottiene a scapito dell'energia interna delle molecole che rimane la stessa ma viene fornita dal termostato. L'energia totale non si conserva infatti si ha uno scambio di calore.

Il programma di simulazione

verifica se sono avvenuti degli urti fra particelle o se alcune particelle hanno urtato contro le pareti o contro lo stantuffo, in tal caso ricalcola le posizioni e le velocità come illustrato precedentemente e rappresenta le posizioni delle particelle, dello stantuffo e i valori dei parametri, in particolare calcola:

T = U / n

V = l * h

P=U / V

L = L₀ + P (V-V₀)

Q = Q ₀ + (U-U₀) - ( L - L₀)

S = S₀+ (Q-Q₀) / T

Istruzioni per l'uso

per eseguire una trasformazione isoterma o adiabatica si agisce sulla massa dello stantuffo ( tasti M+, M-)

per le trasformazioni isocora o isobara si agisce sui tasti (T+, T- )

Nella parte sinistra sono vivibili le molecole che si muovono all'interno del recipiente e urtano tra di loro e contro le pareti.

Nella parte destra si trovano sei scale graduate che permettono di leggere

I valori numerici di queste grandezze vengono anche scritti in alto per comodità e per consentirne la lettura anche nel caso le misure esulino dalle scale graduate.

Tutte le misure vanno effettuate in condizioni di equilibrio, tuttavia anche in questo caso permangono delle fluttuazioni inevitabili. Conviene effettuare più misure nelle stesso stato, assumere come valore più probabile il valore medio e come incertezza le scarto quadratico medio.

Nelle trasformazioni isoterme pressione e volume sono direttamente proporzionali

P V = costante

Per verificare questa legge posizionare il selettore in isoterma, scegliere il minimo raggio delle molecole, portare lo stantuffo nella parte alta del cilindro, attendere che il sistema sia in equilibrio, prendere nota dei valori di P e di V, ripetere la misura più volte nello stesso stato e calcolare la media dei prodotti PV e lo scarto quadratico medio che indica la semiampiezza dell'intervallo di incertezza. Aumentare la pressione, agendo su M+ qualche volta ma lentamente, attendere che il sistema si riposizioni in equilibrio, prendere nota dei valori di P e di V, Ripetere l'operazione più volte come in precedenza. Verificare che i gli intervalli di incertezza dei valori medi di PV ottenuti ammettano un'intersezione comune.

Nelle trasformazioni isobare la temperatura e il volume sono direttamente proporzionali:

V / T =costante

Si procede in modo analogo alla legge di Boyle con la sola differenza che per le trasformazioni isobare si modifica la temperatura e che la legge è di proporzionalità diretta anziché inversa.

Secondo La legge di Avogadro il volume occupato dal gas non dipende dal tipo di gas ma solo dalla pressione, dalla temperatura.

Si effettua la misura dei parametri termodinamici P,V,T in condizioni di equilibrio, si cambia il gas, scegliendo nella seconda finestra un altro valore di m, e si verifica che a parità di pressione e temperatura il volume non è cambiato, anche in questo caso effettuare più misure nello stato di equilibrio e calcolare il valore medio e lo scarto. Verificare infine che i volumi trovati hanno una intersezione comune.

Si lascia allo studente la ricerca del metodo per la verifica, in particolare si verifichi che il valore di k è 1.

Misura dei calori specifici a pressione costante e a volume costante

Per determinare il calore specifico a pressione costante si deve selezionare la trasformazione adiabatica, azzerare il valore del calore premendo il tasto Q = 0,tenere conto delle temperatura iniziale, effettuare la trasformazione modificando la temperatura, prendere nota del nuovo valore di temperatura e del calore, calcolare il rapporto tra il calore e la differenza delle temperature, quello che si trova è la capacità termica del gas, dividere infine per il numero delle molecole n. Ripetere diverse volte l'operazione e calcolare la media e lo scarto, verificare che il valore trovato teoricamente rientra nell'intervallo di incertezza errore trovato sperimentalmente.

Il ciclo Otto viene considerato in modo ideale; come se fosse realizzato da un motore reversibile, pertanto non è una vera rappresentazione del ciclo reale del motore a scoppio, in particolare consideriamo solo le fasi cicliche: adiabatiche ed isocore, senza prendere in considerazione l'aspirazione e l'espulsione.