Effetto fotoelettrico
d
i Massimo Fantinrevisione 2003
Uso del programma di simulazione
L'effetto fotoelettrico consiste nell'emissione di elettroni da un catodo metallico quando è illuminato da una radiazione sufficientemente energetica ovvero da una radiazione di lunghezza d'onda sufficientemente corta (raggi ultravioletti o, in alcuni casi radiazioni luminosa).
Sperimentalmente si vede che l'effetto fotoelettrico segue le seguenti leggi:
Questo fenomeno ha avuto , nella storia della fisica moderna grande importanza perché, da quando fu scoperto, tutti i tentativi fatti dai maggiori fisici del tempo per spiegarlo con la fisica classica andarono disattesi, fino a quando, Einstein nel 1905, facendo ricorso al concetto di discontinuità, suppose che anche l'energia trasportata da un'onda elettromagnetica fosse distribuita in pacchetti detti fotoni o quanti di luce di energia proporzionale alla frequenza della radiazione incidente E = h f dove h rappresenta la costante di Plank, ognuno di questi fotoni, interagendo con un elettrone del metallo cede tutta la sua energia, se questa è maggiore del lavoro di estrazione emerge dal metallo con energia cinetica
1/2 m v2= h f -E0 dove E0 indica il lavoro di estrazione. Se invece hf < E0 l'elettrone, non avendo energia sufficiente non riesce ad uscire dal metallo quindi non si ha emissione.
Con questa ipotesi si possono spiegare le tre leggi dell'effetto fotoelettrico.
Uso del programma di simulazione
Il programma consente di simulare l'effetto fotoelettrico mediante un apparato formato da un tubo a vuoto con due elettrodi, un catodo che può essere illuminato con una radiazione di lunghezza d'onda variabile e di intensità variabile, e un anodo che raccogli gli elettroni emessi dall'anodo, tra gli elettrodi è applicata una d.d.p. variabile tra un valore negativo ed uno positivo. E possibile misurare oltre alla d.d.p., la frequenza della radiazione f e l' intensità luminosa E, anche la intensità di corrente con la quale gli elettroni giungono all'anodo. Tutte le grandezze in gioco sono espresse in unità del S.I. ( Occorre fare attenzione ai fattori moltiplicativi indicati )
L'uso è molto semplice perché la variazione dei parametri viene fatta trascinando con il mouse gli appositi variatori
d.d.p V si trascina il cursore del potenziometro, é espressa in Volt e può variare da -15 V a 15 V.
Intensità luminosa E si variano con l' apposito cursore a destra ed è espressa in Watt/m2 x104
La Frequenza f si varia con l'apposito cursore a destra ed è espressa in Hz x 1013
L'intensità di corrente I è espressa in Ampere ed è misurabile con l'amperometro a portata variabile automaticamente
Verifica delle leggi dell'effetto fotoelettrico citate precedentemente mediante il programma di simulazione
Si ha emissione elettronica solo se la radiazione ha una frequenza superiore ad una frequenza di soglia f0 che dipende dal metallo.
L'energia cinetica degli elettroni dipende dalla frequenza della radiazione e non dalla intensità della radiazione luminosa incidente
Si fissa il valore dell'intensità luminosa ad un valore arbitrario e lo si mantiene costante per tutta la prova, si pone al massimo il valore della frequenza e abbassando gradatamente la tensione (agendo sul reostato) si giunge fino al valore in cui la corrente cessa ( questa operazione deve essere fatta lentamente e con attenzione perché la corrente cessa improvvisamente. E' necessario determinare con assoluta precisione il valore in cui questo avviene) si segna in una tabella i valori di frequenza e di tensione DV che è negativo. Si ripete l'operazione per un altro valore di frequenza, e cosi via, diminuendo sempre i valori della frequenza fino al punto in cui, con tensione zero non si ha più passaggio di corrente, il valore di frequenza più alto in cui avviene questo è la frequenza di soglia.
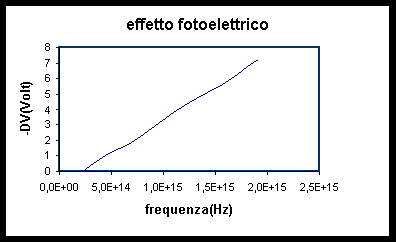
Per verificare la seconda legge tracciamo il grafico della -DV rispetto alla frequenza e osserviamo che l'energia cinetica degli elettroni è direttamente proporzionale alla tensione perché si suppone che ciascuno elettrone non incontri altre particelle lungo il suo cammino, questo è possibile perché si suppone che nel dispositivo ci sia il vuoto. Il grafico è quello di una retta non passante per l'origine la cui equazione è determinabile sperimentalmente. K = h f - Wo dove Wo è il lavoro di estrazione Wo=h fo mentre K = e DV dove e è la carica dell'elettrone, l'equazione si può quindi scrivere: eDV= h f-h fo , che può essere scritta h/e = DV/(f-fo). Questa formula ci permette di calcolare il valore del rapporto tra la costante di Plank e la carica dell'elettrone e verificare che tale rapporto è compatibile con quello che si può trovare sui libri come si vede nella tabella riportata di sotto.
I valori riportati sono effettivamente determinati da misure fatte con il programma di simulazione e hanno permesso di determinare la frequenza di soglia fo = 2.2 x1014 Hz, il rapporto h/e = (4.2± 0.1)x10-15 compatibile con quello noto 4.14x10-15 e inoltre l'equazione eDV=h(f-fo) che mette a confronto le frequenze con le d.d.p.
|
frequenza |
-DV |
f - fo |
DV/(f-fo) |
|
2,20E+14 |
0 |
0,00E+00 |
|
|
4,40E+14 |
1 |
2,20E+14 |
4,55E-15 |
|
6,60E+14 |
1,75 |
4,40E+14 |
3,98E-15 |
|
8,80E+14 |
2,75 |
6,60E+14 |
4,17E-15 |
|
1,10E+15 |
3,75 |
8,80E+14 |
4,26E-15 |
|
1,32E+15 |
4,75 |
1,10E+15 |
4,32E-15 |
|
1,54E+15 |
5,5 |
1,32E+15 |
4,17E-15 |
|
1,76E+15 |
6,5 |
1,54E+15 |
4,22E-15 |
|
1,91E+15 |
7,25 |
1,69E+15 |
4,29E-15 |
|
Media h/e |
4,2E-15 |
||
|
Scarto |
1,6E-16 |
||
|
h= |
6,63E-34 |
||
|
e= |
1,60E-19 |
h/e vero= |
4,14E-15 |
I valori trovati vengono riportati nel grafico

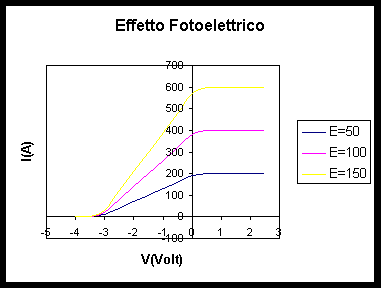
Il numero degli elettroni emessi aumenta all'aumentare della intensità della radiazione secondo una legge di proporzionalità diretta..
Si fissa un valore di intensità luminosa e, mantenendolo costante si varia la V, a partire da un valore negativo che annulli la corrente, si aumenta la V fino a raggiungere la saturazione ( la intensità di corrente non aumenta più) . Si modifica il valore dell'intensità luminosa E, per esempio si raddoppia e si ripete l'operazione per almeno altre due volte. Si traccia i grafici delle intensità di corrente in funzione della V, e si nota che le correnti sono, a parità di V applicata, proporzionali alla intensità luminosa.
I valori di seguito riportati sono stati ottenuti dal programma di simulazione. Poiché il sistema è piuttosto instabile ( L'indice dell'amperometro oscilla parecchio, è bene tenerlo sotto osservazione per un po' di tempo e assumere come valore il valore medio delle posizioni assunte. Il motivo dell'instabilità è dovuto al fatto che la simulazione avviene in modo discreto, si utilizza un certo numero di elettroni che escono dal metallo del catodo, l'energia di questi elettroni è distribuita in modo statistico e l'amperometro misura il numero degli elettroni che giungono all'anodo, poiché il numero degli elettroni, per motivi di calcolo non può essere troppo grande, sono molto evidenti le variazioni statistiche che si verificano, questo si traduce in una ampia variabilità nel numero degli elettroni che giungono all'anodo a anche con gli stessi parametri iniziali ( intensità luminosa E , frequenza, d.d.p. V )
|
Effetto fotoelettrico f=10E15 Hz |
||||
|
E=50 x10^4 |
E=100x10^4 |
E=150x10^4 |
||
|
V(volt) |
I(A) |
I(A) |
I(A) |
|
|
-4 |
0 |
0 |
0 |
|
|
-3,5 |
0 |
0 |
0 |
|
|
-3 |
10 |
20 |
30 |
|
|
-2,5 |
40 |
80 |
120 |
|
|
-2 |
70 |
140 |
210 |
|
|
-1,5 |
100 |
200 |
300 |
|
|
-1 |
130 |
260 |
390 |
|
|
-0,5 |
160 |
320 |
480 |
|
|
0 |
190 |
380 |
570 |
|
|
0,5 |
200 |
400 |
600 |
|
|
1 |
200 |
400 |
600 |
|
|
1,5 |
200 |
400 |
600 |
|
|
2 |
200 |
400 |
600 |
|
|
2,5 |
200 |
400 |
600 |
|
I valori ottenuti vengono riportati nel grafico seguente che rappresentano un comportamento simile a quello reale.