di Massimo Fantin
E' dato un triangolo ABC, tracciate la circonferenza circoscritta al triangolo e la circonferenza di centro il punto C e passante per B, sia A' l'ulteriore intersezione con la circonferenza circoscritta e K il punto di intersezione tra la retta AA' ed il lato AC del triangolo. Allora, il quadrato del lato AC è equivalente al rettangolo di lati CK e l'intero lato BC.
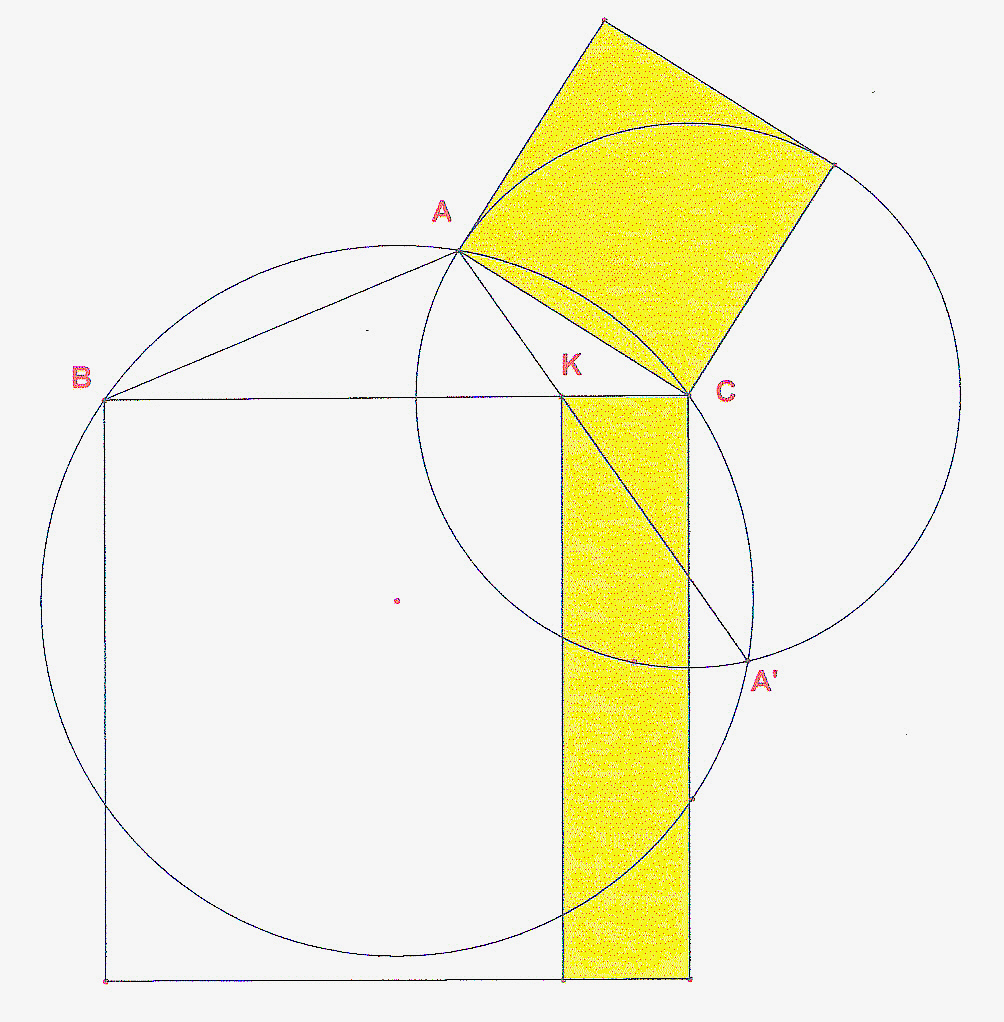
Dimostrazione:
Gli archi AC e CA' sono uguali perché le corde CA e CA' sono
raggi della cfr di centro C, pertanto gli angoli A'AC e l'angolo
ABC sono uguali perché angoli alla cfr che insistono su archi uguali.
I triangoli BCA e ACK sono simili perché hanno l'angolo in C in comune e
abbiamo inoltre dimostrato che gli angoli ABC =CAK. Per la similitudine
vale la proporzionalità tra i lati:
BC : AC = AC: CK, che dimostra il teorema.
E' evidente che questo generalizza il primo teorema di Euclide in quanto se il triangolo ABC è rettangolo in A, il centro della circonferenza circoscritta cadrebbe sul lato BC e la corda AA' risulterebbe perpendicolare al diametro AC.
Sia ABC un triangolo generico, si determini la circonferenza circoscritta e sia A' il punto sulla circonferenza in modo che AC=A'C. Si conduca la corda AA' che incontra in K il lato BC.
Analogamente si conduca inoltre la corda AA'' in modo che AB=BA'' e sia H il punto di intersezione di AA'' con BC
allora il quadrato di AK è equivalente al rettangolo di lati CK e HB.
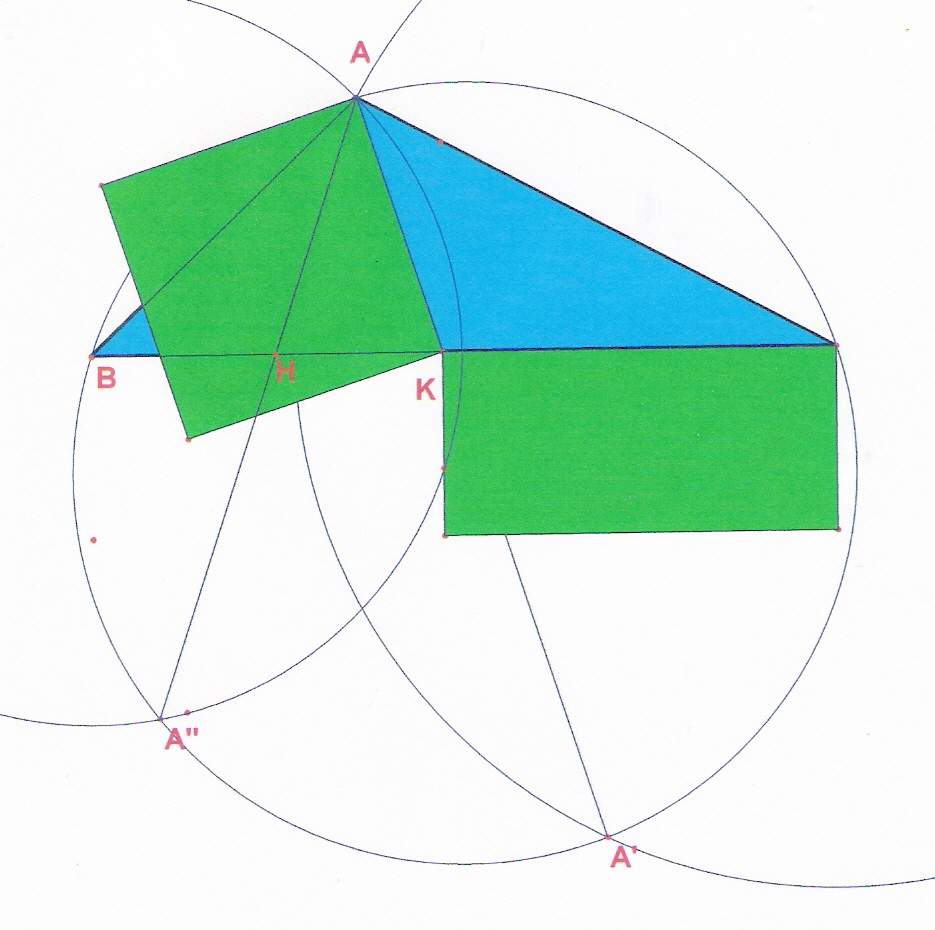
Dimostrazione
Poichè gli archi AC e CA' sono uguali, gli angoli A'AC= ABC , segue che i triangoli BCA e AKC sono simili avendo due angoli uguali.
Per l'analoga costruzione anche BAC e BHA sono simili . Pertanto i triangoli BHA e AKC sono simili essendo entrambi simili di uno stesso triangolo, pertanto BH/HA=AK/KC ma essendo AK=AH perchè gli angoli in K e in H sono uguali segue la tesi.
Anche questo teorema generalizza il secondo di Euclide infatti se l'angolo in A è retto H e K vengono a coincidere.