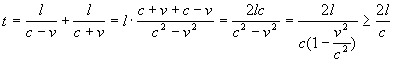
Problemi dei due cani
(introduzione alla relatività ristretta)
Primo Problema
Un battaglione di soldati disposti in quadrato di lato l si muove con velocità costante v mentre un cane procede parallelamente ad esso avanti ed indietro per tutta la lunghezza del battaglione alla velocità c>v.
Quanto tempo impiega a compiere un andirivieni completo?
Se il battaglione di soldati è fermo il tempo impiegato è spazio/ tempo t = 2l/c
Per risolvere questo problema in generale, consideriamo le velocità relative del cane rispetto al battaglione che sono c-v quando il cane procede nello stesso verso dei soldati e c+v quando procede in verso contrario. Il tempo complessivo impiegato dal cane per compiere un andirivieni completo sarà data da:
![]()
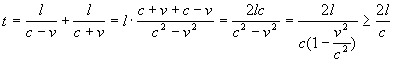
Come si vede dall'ultima disuguaglianza il tempo impiegato dal cane è maggiore se il battaglione di soldati è in movimento, rispetto a quello che impiegherebbe se fosse fermo.
Secondo Problema
Un battaglione di soldati disposti a quadrato di lato l si muove con velocità costante v mentre un cane procede perpendicolarmente al movimento dei soldati e per tutta la sua lunghezza del battaglione alla velocità c > v.
Quanto tempo impiega a compiere un andirivieni completo?
Per risolvere questo secondo problema, leggermente più difficile del precedente per il fatto che le velocità da comporre hanno direzione perpendicolare e non parallela, utilizziamo una nuova variabile S che indica lo spazio che il cane deve percorrere complessivamente in un andirivieni , per il teorema di Pitagora
(S/2) 2 = l2 + v2t2
Questa equazione posta a sistema con S = c t ed eliminando S si ottiene
c2t2 = 4l2 + v2t2, risolvendo in t si ha:
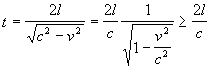
Come per il problema precedente il tempo impiegato dal cane è maggiore di quello che impiegherebbe se il battaglione fosse fermo.
Terzo problema
Quale dei due cani dei problemi precedenti impiega meno tempo per fare il suo percorso?
Il problema si riduce a osservare che
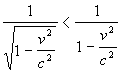
infatti v<c pertanto 0<v/c<1, allo stesso modo il quadrato e anche 1-v2/c2, la radice quadrata di un numero minore di 1 è maggiore del numero stesso e l'inverso della radice è minore.
Conclusione Se i due cani partono contemporaneamente da uno stesso angolo del battaglione e procedono in direzioni perpendicolari per poi tornare al punto di partenza, il primo a ritornare è il cane del secondo problema, quello che procede perpendicolarmente al battaglione dei soldati.
Quarto problema
Calcolare la differenza dei tempi impiegati dai due cani per fare il loro percorso
Osservato precedentemente che il secondo cane è più veloce del primo, il problema si riduce a calcolare:
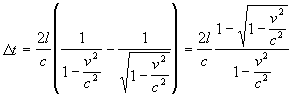
per fare questo si fa un'ipotesi semplificatrice, si suppone che v sia molto minore di c, ovvero che il cane sia molto più veloce dei soldati, in tal caso 1-v2/c2 sarà piuttosto vicino ad 1 e varrà l'approssimazione di Taylor:
![]()
sostituendo nella precedente e supponendo v2/c2 trascurabile rispetto ad 1 ha:
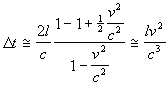
Osservazione finale
I problemi dei due cani in realtà sono una metafora dell'esperimento di Michelson Morley:
I cani rappresentano i due raggi di luce inviati perpendicolarmente.
Il battaglione dei soldati rappresenta l'apparato sperimentale che si muove solidalmente alla Terra.
Il terreno sul quale marciano i soldati e corrono i cani rappresenta l'"etere luminifero" che ipotizza il sistema di riferimento privilegiato rispetto al quale le luce dovrebbe assumere la velocità c.
L'intervallo di ritardi tra i due raggi di luce Dt rappresenta il ritardo al quale dovrebbero essere giunti i due raggi di luce. ( Osserviamo che le approssimazioni fatte sono valide perché la velocità della Terra è molto inferiore rispetto a quella della luce)
Calcoliamo infine Dt sostituendo i valori numerici c = 3*108 m/sec, v = 3*104 m/sec, l =10 m.
D
t = 10*9* 10 8 / (27 *1024) @ 3.3*10-16 secin un tempo così piccolo la luce percorre
D
S = c Dt = 3*108 * 3.3 * 10-16=10-7 m = 0.1 m m.Considerato che la lunghezza d'onda della luce è inferiore al m m, un tale sfasamento sarebbe dovuto essere rilevabile dall'interferometro a disposizione degli scienziati americani, essi non riscontrarono alcuno sfasamento tra i due raggi di luce e ciò stava a significare che la velocità della luce nel vuoto è indipendente dal sistema di riferimento inerziale considerato cioè non esiste un sistema di riferimento privilegiato e nemmeno l'"etere luminifero".