HOME

Considerazioni, chiarimenti e complementi su “L’ABC della relatività” di Bertrand Russel

Il tatto e la vista, il cielo e la terra.

Incipit del libro: Tutti sanno che Einstein ha fatto qualcosa di sorprendente ma pochi sanno che cosa abbia fatto esattamente.

Il motivo è molto semplice, perché ciò che ha fatto è comprensibile solo a pochi, in tanti ambienti si sente parlare di relatività, ma per capire veramente qualche cosa della relatività non basta certo leggere un libro divulgativo, forse comprenderemmo solo alcune idee che appaiono più fantascientifiche che scientifiche e spesso possono essere fuorvianti rispetto al vero significato.

La teoria della relatività dipende dalla capacità che abbiamo di liberarci dalle nozioni che sono utili nella vita ordinaria, come per esempio la proprietà che hanno i corpi di essere localizzati in un punto della superficie terrestre.

Se facciamo un viaggio da BO a FI pensiamo che sia il treno sul quale ci troviamo a spostarsi da una città all’altra e non la città di FI a venirci incontro, siamo certamente noi a spostarci e pensiamo che la città di Firenze rimanga sempre allo stesso posto.

Dal punto di vista della relatività è lo stesso dire che siamo noi a spostarci verso Firenze o è Firenze che si sposta verso di noi. Se le città fossero in moto l’una rispetto all’altra non ci meraviglieremmo di vedere la cosa in quest’ultimo modo. Come succede per le stelle e i pianeti che si muovono ben più velocemente di un treno terrestre.

L’idea che la città di Firenze rimanga ferma nello stesso posto dipende dalle dimensioni del nostro percepire il mondo. Se guardassimo la nostra Terra da un pianeta lontano ci renderemmo conto che Firenze si muove seguendo una traiettoria piuttosto complicata, il nostro treno si muoverebbe di un moto leggermente diverso ma altrettanto complicato e, dopo un certo tempo si incontrerebbero.

Se poi fossimo grandi come un elettrone non avrebbe senso pensare che la stazione di FI rimanga ferma al suo posto infatti, guardando con gli occhi degli elettroni quella che noi chiamiamo città in realtà è formata da innumerevoli particelle che si muovono in tutte le direzioni, secondo traiettorie prevalentemente casuali, e la città di Firenze non sarebbe lì ad aspettarci.

Altro concetto per cui la fisica terrestre differisce dall’astronomia è per il concetto di forza che è dovuto all’azione muscolare sui corpi o, nel caso degli urti dal contatto tra un corpo e l’altro. Per i corpi celesti non c’è contatto eppure si influenzano a vicenda. Per Newton doveva esistere qualche cosa di meccanico che agiva tra i due corpi. In realtà , secondo la teoria della relatività è il concetto di forza che viene a cadere. Il pianeta movendosi è attento solo a ciò che si trova intorno al punto in cui si trova, alla curvatura dello spazio, in quel punto preciso, non gli interessa se questa è dovuta a pianeti o all’accelerazione o ad altro.

Quel che succede e quel che si osserva.

Tutto è relativo, sembra il motto della teoria della relatività ma se tutto fosse relativo non ci sarebbe nulla con cui stare in relazione.

Tutto è relativo all’osservatore. Per alcune grandezze è evidente la relatività rispetto all’osservatore: La velocità è evidente che è relativa all’osservatore ma secondo la teoria della relatività anche la lunghezza degli intervalli di tempo e le misure delle lunghezze dipendono dall’osservatore.

La fisica però si occupa di quelle caratteristiche che, sono comuni a tutti gli osservatori che esaminano un dato fenomeno.

Secondo la teoria della relatività rimane invariata la velocità delle luce come si evince sperimentalmente dall’esperimento di Michelson e Morley

La velocità della luce

Esempi strani:

1)Se un corpo in movimento emette luce, resterà sempre al centro delle sue onde luminose.

Questo non succede per le onde superficiali o sonore mentre per la luce si perché la velocità della luce è indipendente dal sistema di riferimento, naturalmente questo è vero solo per l’osservatore che si muove con la sorgente luminosa.

2) Se uno spara un proiettile d’artiglieria, questo si muove più veloce del suono per cui chi si trova vicino alla traiettoria vedrà prima il proiettile e poi sentirà il colpo. Un osservatore sul proiettile non sentirebbe mai il colpo. Se il suono si comportasse come la luce, l’osservatore udirebbe il colpo esattamente come se fosse fermo. Se cento metri più avanti fosse posto uno schermo per fare l’eco che si muove col proiettile l’osservatore sentirebbe l’eco esattamente come se fosse fermo.

3)Supponiamo ora di essere su un treno e dal vagone di coda spariamo un colpo, nella locomotiva è fissato uno schermo riflettente a 333m dal luogo dello sparo ( 333 è lo spazio percorso dal suono in un secondo ). Se il treno è fermo l’osservatore sente l’eco dopo 2 secondi mentre se il treno si muove alla velocità di 1/12 di quella del suono l’eco si sente dopo un tempo di 2+2*(1/12)² =2+1/72 di secondo.

Se il suono si comportasse come la luce l’eco giungerebbe sempre dopo due secondi indipendentemente dalla velocità del treno.

4) Su una pedana mobile del supermercato si arriva in cima più in fretta se si cammina, ma se la pedana si muovesse alla velocità della luce sarebbe indifferente: stare fermi, camminare verso l’alto o verso il basso, si arriverebbe sempre nello stesso momento.

5) Se viaggiate in autostrada ai 120km/h e vi supera un’auto ai 150 km/h ( supponendo che le velocità rimangano costanti) potete dire che dopo due minuti l’auto disterà da voi 2*(150-120)/60 = 1km. Mentre se la seconda macchina la vedete sfrecciare alla stessa velocità nella corsia opposta dopo due minuti sarà a 2*(150+120)/60= 9 km da voi.

Se la seconda macchina viaggiasse alla velocità della luce invece dopo un minuto la seconda macchina sarebbe sempre alla stessa distanza da voi indipendentemente dalla vostra velocità e direzione.

Questi esempi ci fanno capire che la relatività conduce a dei risultati molto strani per il nostro modo di vedere il mondo. Per capirci qualche cosa dobbiamo pensare che il tempo scorra diversamente per i due osservatori in moto.

Orologi e strumenti di misura

Prima dell’avvento di Einstein nessuno pensava che lo scorrere del tempo dipendesse dal sistema di riferimento, inoltre si pensava che la contemporaneità tra due fenomeni fosse una caratteristica indipendente dall’osservatore. Secondo la teoria della relatività due eventi A e B possono essere contemporanei per un osservatore mente l’evento A precedere il B per un secondo osservatore e il B precedere l’A per un terzo, senza che si giunga ad alcuna contraddizione.

Dobbiamo innanzitutto definire il concetto di simultaneità: due eventi possono dirsi simultanei rispetto ad un osservatore che si trovi nel punto medio se i due raggi di luce provenienti dai due eventi giungono nello stesso istante.

Non ci meravigliamo del fatto che due eventi per un osservatore possano avvenire nello stesso luogo ma in tempi diversi per un osservatore e luoghi e tempi diversi per un altro. Esempio: quando leggete un giornale nel vostro scompartimento del treno da Firenze a Bologna per il vostro sistema di riferimento tutti gli eventi relativi alla lettura del giornale sono avvenuti nello stesso posto: lo scompartimento, mentre per un osservatore esterno questi stessi eventi sono avvenuti in luoghi diversi.
Ci meravigliamo invece se pensiamo ad eventi che avvengono nello stesso istante ma in luoghi diversi per un osservatore e luoghi e tempi diversi per un altro. Per la relatività spazio e tempo rivestono ruoli simmetrici. ( per capire meglio il concetto vedi esempio successivo)

Distinguiamo tra distanze temporali e distanze spaziali, tra due eventi la distanza è spaziale se anche movendosi alla velocità della luce non è possibile trovarsi in entrambi gli eventi, mentre la distanza tra due eventi è temporale se movendosi a velocità inferiore a quella della luce è possibile essere presente ad entrambi gli eventi. Se la distanza è spaziale esisterà un sistema di riferimento rispetto al quale i due eventi sono simultanei mentre se gli eventi sono temporali esisterà un sistema di riferimento rispetto al quale gli eventi si verificano nello stesso luogo ma in tempi diversi. Gli eventi della nostra vita di tutti i giorni hanno fra loro distanze temporali infatti viviamo in un mondo nel quale le distanze spaziali sono dell’ordine dei km o al più delle migliaia di km sempre di gran lunga maggiori delle distanze temporali che sono dell’ordine dei secondi minuti ore giorni o anni, ricordiamo che un secondo corrisponde a 300.000 km che è quasi la distanza Terra Luna o otto volte la circonferenza terrestre.

Uno potrebbe chiedersi: se nella relatività tutto è relativo c’e qualche grandezza, oltre la velocità della luce che rimane invariato?

La relatività studia appunto questo, infatti potremmo dire che il nome scelto per la teoria di Einstein forse non è proprio il più adatto, infatti sembra mettere in evidenza solo un aspetto senza tener conto dell’altro che invece mira a riconoscere ciò che è invariante rispetto al cambiamento di sistema di riferimento.

L’intervallo-invariante è l’ente matematico che rimane costante esso comprende sia le dimensioni spaziali che quelle temporali pertanto non possiamo più parlare di spazio e di tempo ma di spazio tempo che costituisce un tutt’uno. L’intervallo-invariante può essere di due tipi a seconda se prevale la distanza temporale o spaziale:

temporale ds² = (c dt)² – dx²+ dy²+ dz²

spaziale ds² = dx²+ dy²+ dz²- (c dt)²

La teoria della relatività ristretta

Anche se noi quando pensiamo alla relatività ristretta pensiamo a questioni meccaniche, relative a sistemi di riferimento in moto, in realtà la relatività ristretta nacque da questioni relative all’elettromagnetismo che era stato studiato da Maxwell nell’ottocento a seguito di studi sperimentali di Faraday ed altri. Nell’ottocento si pensava che la luce per propagarsi avesse bisogno di un mezzo che venne chiamato “etere luminifero”, Maxwell che dalle sue equazioni dedusse l’esistenza delle onde elettromagnetiche pensò che lo stesso etere potesse costituire da mezzo di propagazione delle onde elettromagnetiche. A seguito degli esperimenti di Michelson e .Morley del 1889 si cominciò a prendere in considerazione l’ipotese che la velocità della luce, che era stata misurata fin dal Settecento, nel vuoto si propagasse sempre alla stessa velocità, indipendentemente dalla velocità del sistema nel quale si misura. Questo portò con la teoria della relatività a ipotizzare che, non esistendo un sistema di riferimento privilegiato, l’ipotesi dell’etere era incompatibile con l’esperienza pertanto da rifiutare: L’etere non esiste. Ma allora su che cosa si propagano le onde elettromagnetiche? In realtà la risposta è stata data da Einstein con la relatività ristretta ma, era già, in embrione compresa nelle equazioni che Maxwell aveva formulato anni prima, senza che ne fosse accorto, dalle sue equazioni si può appunto dedurre che la velocità della luce non dipende dal sistema inerziale nel quale ci troviamo, o, come dicono i fisici le equazione di Maxwell. sono invarianti per trasformazioni di Lorentz, trasformazioni che furono appunto formulate facendo l’ipotesi che la nel vuoto la velocità della luce fosse indipendente dal sistema inerziale. Le equazioni di Maxwell pertanto dicono molto di più di quello per le quali erano state formulate. La costanza della velocità della luce comportava un capovolgimento così radicale nel modo di vedere il mondo che è difficile da comprendere. La maggiore difficoltà riguarda la relatività del tempo che non scorre allo stesso modo in due sistemi che si muovono uniformemente l’uno rispetto all’altro. Secondo la relatività lo scorrere del tempo in un sistema di riferimento che si muove rispetto a noi con una velocità v è più lento di come scorre nel nostro sistema. Se ci passasse davanti un treno alla velocità di 3/5 della velocità della luce e osservassimo sia i nostri orologi che quelli dei passeggeri vedremmo che mentre nei nostri orologi è passata un minuto (60 secondi) negli orologi dei passeggeri sono passati 75 secondi. Ma la cosa strana è che anche noi, rispetto ai passeggeri ci muoviamo, e per i passeggeri anche i nostri orologi si muovono più lentamente dei loro allo stesso modo. La cosa è perfettamente simmetrica.

Anche la lunghezza del treno è diversa a seconda se la misuriamo con regoli del sistema di riferimento del treno o con regoli del sistema della ferrovia. Se per i viaggiatori il treno è lungo 100 metri per chi sta fermo lungo la linea ferroviaria la lunghezza del treno è soltanto di 80 metri

Le formula esatte per trovare il tempo proprio e la lunghezza propria in un sistema di riferimento conoscendo il nostro tempo che chiamiamo to e la nostra lunghezza è data da:

t = to / Ö(1-(v/c)²)

l = lo * Ö(1-(v/c)²)

nel nostro caso v/c=3/5 pertanto t = to*5/4 l=lo*4/5=80 metri come avevo anticipato.

Le trasformazioni di Lorentz permettono di “trasformare” le coordinate spazio-temporali di un sistema di riferimento in un altro in moto rettilineo uniforme rispetto al primo e sono state studiate da Lorentz appunto per via matematica supponendo come postulato appunto la costanza della velocità della luce. Nel caso del moto unidimensionale sono date da

X=( x - v t) / Ö( 1 - (v/c)²)

T= (t - v x/c²) / Ö( 1 - (v/c)²)

Dove x,t sono le coordinate spaziotemporali del nostro sistema di riferimento mentre X, T sono quelle del sistema in movimento con velocità costante v, mentre c rappresenta la velocità della luce.

Esempio numerico un po’ difficile dal punto di vista concettuale

Per semplicità usiamo un sistema di unità di misura nel quale si considerino unitarie il secondo per il tempo, il secondo-luce per lo spazio e la velocità della luce per la velocità, con questa precisazione non scrivo le unità di misura.

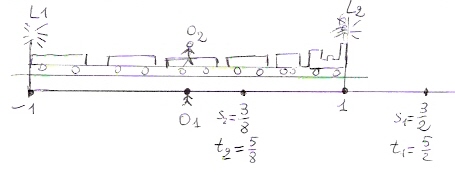
Supponiamo che il treno relativistico lungo 2 secondi luce ( immaginiamo naturalmente di vivere in un mondo supergigante perché sulla terra un treno così lungo non ci sta) viaggi alla velocità di 3/5 da ovest a est. Il moto è seguito da due osservatori: O1 si trova in terra lungo la linea ferroviaria, O2 al centro del treno. Una unità spaziale a est e una a ovest sono collocati due fari che emettono un lampo quando la testa del convoglio e la coda giungono in prossimità dei rispettivi fari. Nell’istante nel quale i due osservatori si trovano uno vicino all’altro scoccano i lampi perché inizio e fine coincidono con i fari. ( è lecito parlare di simultaneità quando si considerano eventi che avvengono nello stesso luogo)

Osserviamo ora che cosa succede per l’osservatore O1 a terra. La luce si muove a velocità 1 dal faro all’osservatore pertanto le velocità relative della luce rispetto ala treno in movimento saranno di

v1=1-3/5=2/5 per il lampo L1 proveniente da ovest cioè dalla coda del treno e

v2=1+3/5=8/5 per il lampo L2 provenente da est cioè dalla testa del treno,.

Inoltre per l’osservatore O1 l’osservatore O2 vedrà i lampi di luce al tempo
t1=s1/v=1/(2/5)=5/2 mentre

t2 = s2/v2 =1/(8/5)=5/8. ( attenzione che questi sono i tempi di O1, per O2 i tempi sono diversi)

L’osservatore O1 vedrà il lampo L1 dalla coda nella posizione

s1 =v1*t1=3/5*5/2=3/2 mentre il lampo L2 giungerà ad O1 quando si trova nella posizione s2=v*t2=3/5*5/8=3/8.

Il rapporto tra i tempi occorrenti ai due lampi per giungere all’osservatore O1 stanno nel rapporto t1/t2=4.

Fin qui abbiamo ragionato in modo classico senza considerare gli effetti relativistici della dilatazione del tempo e della contrazione delle lunghezza ma solo considerando la velocità della luce finita.

Per passare ora ai tempi propri dell’osservatore O2 sul treno applichiamo le trasformazioni di Lorentz nelle quali sostituendo c=1 e v=3/5 diventano:

X=5/4( x -3/5 t)

T=5/4(t -3/5 x)

E i trasformati degli eventi spazio-temporali a conti fatti sono:

I due lampi che scoccano per O1 in ( x=1, t=0 ) e (x= - 1,t = 0) si trasformano in

(X=5/4, T=-3/4) e (X=-5/4, T= ¾)

le percezione degli stessi lampi che per =1 sono (x=3/8, t=5/8) si trasformano in

(X=0,T=1/2) e ( X=0,T=2).

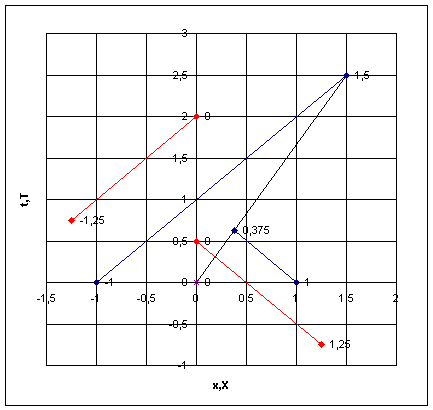
Il grafico qui riportato ci mostra la situazione sia dal punto di vista dell’osservatore O1 a terra ,rappresentato dalle linee si colore blu che dal punto di vista dell’osservatore O2 sul treno rappresentato dalle linee rosse. Mentre la linea nera che parte dall’origine rappresenta il moto del treno visto sempre dall’osservatore a terra. I valori numerici sono già stati descritti.

Dal grafico si vede che mentre per l’osservatore O1 i lampi partono contemporaneamente e da posizioni simmetriche, i tempi di percorrenza della luce sono uno quattro volte l’altro, per l’osservatore sul treno sono uguali (come si vede dalle lunghezze delle linee rosse che hanno la medesima lunghezza).

Non si conserva la simultaneità degli eventi infatti per l’osservatore O1 (blu) i lampi sono emessi contemporaneamente mentre giungono in tempi e luoghi diversi. Per l’osservatore O2 i lampi partono in tempi e luoghi diversi ma simmetrici rispetto all’evento iniziale (origine), il lampo di testa è partito nel passato e quello di coda partirà nel futuro rispetto al passaggio all’origine; giungono nello stesso luogo, ma in tempi diversi. Hanno percorso, spazi uguali in tempi uguali. Da questo si verifica che la velocità della luce è costante nei due sistemi di riferimento, la velocità nel grafico è rappresentata dall’anticoefficiente angolare, le rette corrispondenti al moto della luce hanno tutte coefficiente uno pertanto hanno tutte la stessa velocità.

Esercizio ulteriore per comprendere la relatività del tempo e della simultaneità

Un’ astronave ci sfrecci davanti alla velocità ( secondo il nostro sistema di riferimento ) di 3/5 della velocità della luce) la lunghezza dell’astronave ( sempre secondo il nostro sistema di riferimento è di un secondo luce). All’interno dell’astronave un fotone di luce viene riflesso avanti e indietro all’interno dell’astronave da due specchi situati all’inizio e alla fine dell’astronave . Dal nostro punto di vista il fotone viaggia alla velocità della luce mentre la velocità dell’astronave si somma o si sottrae, pertanto quando il fotone si muove da dietro a davanti la velocità relativa del fotone rispetto all’astronave sarà di 1-3/5= 2/5 mentre quando il fotone torna indietro la velocità relativa è 1+3/5=8/5 pertanto i tempi che tale fotone impiega per andare da coda a testa e da testa a coda sono rispettivamente di 5/2 e di 5/8, questo significa che i due tempi sono assai diversi per l’osservatore esterno.

La cosa molto strana, in un problema come questo è che, dal punto di vista dell’osservatore che si trova sull’astronave i tempi di andata e ritorno sono gli stessi. Per calcolare questi tempi usiamo le trasformate di Lorentz che ci permettono di passare dalle coordinate spaziotemporali secondo l’osservatore esterno a quelle dell’osservatori interno.

Le trasformazioni di L. semplificate dal fatto che c=1 diventano

X = (x - v t)/ Ö(1-v²)

T = ( t - v x )/ Ö(1-v²)

Che posto v=3/5 diventano

X = 5/4 (x - 3/5 t)

T= 5/4 (t - 3/5 x)

Che produce la tabella seguente

x	t	X	T
0	0	0	0
2,5	2,5	1,25	1,25
1,875	3,125	0	2,5
4,375	5,625	1,25	3,75
3,75	6,25	0	5
6,25	8,75	1,25	6,25
5,625	9,375	0	7,5
8,125	11,875	1,25	8,75
7,5	12,5	0	10

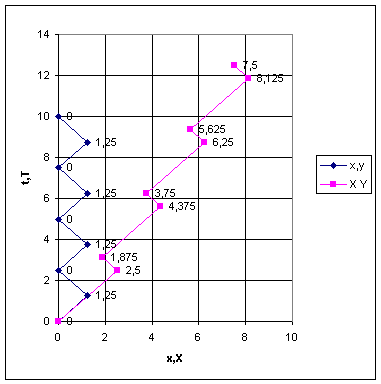
Dal grafico a sinistra si evidenzia la perfetta simmetria dei tempi e degli spazi visti dall’osservatore sull’astronave mentre per l’osservatore esterno si ha una asimmetria

Altro esempio : il paradosso dei gemelli. ( aggiunta 2007)

Due gemelli si separano. Uno rimane tranquillo sulla Terra, mentre l'altro si allontana dal primo ad una velocità molto alta, confrontabile con quella della luce, dopo un certo numero di anni decide di ritornare, fa inversione di marcia e ritorna verso il primo fratello, sempre con velocità molto alta. Quando i due gemelli si incontrano, il secondo, che si è allontanato e poi riavvicinato è più giovane del primo perché il tempo per i due gemelli è trascorso in modo diverso.

La verifica sperimentale, galileiana, di questo strano fenomeno è stata fatta usando al posto dei gemelli due orologi estremamente precisi e perfettamente sincronizzati. uno di essi è stato fatto viaggiare per un certo tempo di un moto accelerato e dopo un certo tempo è ritornato a terra e confrontato con il primo orologio rimasto sempre fermo. Il tempo segnato dall'orologio che ha subito accelerazione è minore, seppure di poco da tempo segnato dall'orologio rimasto a terra.

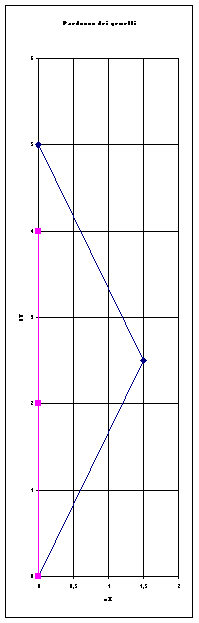
Lo chiamiamo paradosso perché in un primo momento sembrerebbe che la posizione dei due gemelli , od orologi che siano, sia simmetrica e quindi che, se un orologio è in anticipo rispetto all'altro lo debba essere anche il primo, poiché la relazione di anticipo è antisimmetrica dovrebbero segnare lo stesso tempo. La rottura della simmetria è dovuta al fatto che il secondo gemello, per tornare a confrontarsi con il primo a, ad un certo punto deve tornate indietro subendo una forte accelerazione.

Per risolvere questo paradosso dobbiamo anche qui applicare le trasformazione di Lorentz ed esaminare i tempi nei due sistemi di riferimento.

Per comodità consideriamo valori numerici del moto, semplici da calcolare.

Un primo orologio rimane nel sistema O1 inerziale per tutto il tempo dell'esperimento mentre l'altro orologio si muove per 3/2 di secondo alla velocità di 3/5 della velocità della luce v = 3c/5 in allontanamento.

Per la seconda metà del viaggio si muove con velocità -3c/5 cioè in ravvicinamento.

Rispetto al sistema di riferimento inerziale O1 gli spostamenti del gemello sono indicati nel grafico a sinistra in blu: parte dall'origine (0,0) e spostandosi alla velocità di 3/5 si troverà all'istante 5/2 alla distanza 3/2 dal gemello, le coordinate sono (x,t) ( 3/2,5/2). A questo punto rientra spostandosi alla velocità -3/2 per ritornare al punto di partenza in (0,5).

Per il gemello in movimento applichiamo le trasformazioni di Lorentz al punto (0,0) ottenendo banalmente (0,0) e al punto (3/2,5/2) dell'evento l'inversione di marcia.( naturalmente questa inversione non potrà avvenire istantaneamente tuttavia anche se si considera una decelerazione regolare le cose non cambiano di tanto)

( (3/2-3/2*5/2 ) / (4/5) , (5/2-3/5*3/2)/(4/5) )=(0,2)

Che sta ad indicare che, mentre che per il gemello O1 è passato un tempo pari a 5/2 per O2 il tempo trascorso è stato soltanto di 2 .( grafico rosso)

A questo punto si deve analizzare il percorso di ritorno durante il quale la velocità è contraria, per la simmetria del problema evitiamo i calcoli che portano agli stessi risultati. Pertanto in conclusione per il gemello O1 è trascorso un tempo paria 5 unità ( percorso blu) , per O2 in movimento solo 4 unità.

Osservazione: Si osserva che questo fenomeno è il duale di un fatto che ben conosciamo e di cui nessuno si meraviglia, scambiamo il tempo con lo spazio. Se per andare da un punto A ad uno B se ci si muove in linea retta si percorre un tragitto più corto di un altro viaggiatore che va per una via tortuosa. Per i tempi le cose vanno a rovescio infatti il tempo più lungo è quello del gemello che percorre uno spostamento spazio-temporale rettilineo ( inerziale) non quello che fa un percorso tortuoso, come invece succede per li spostamenti spaziali a cui siamo abituati.