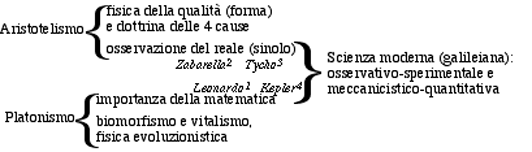
1. Leonardo da Vinci (1452-1519): da posizioni neoplatoniche, afferma l’importanza della matematica e anticipa il concetto galileiano di inerzia, pensando alla vis viva.
Mentre l’importanza che egli dà all’osservazione è conseguenza della pratica pittorica (uso della prospettiva) come anche della sua attività di ingegnere (idraulico e meccanico) e di architetto (civile e militare), ma non di scelte o posizioni filosofiche: non a caso lui stesso ama definirsi «homo sanza littere».

«Nessuna umana investigazione si po’ dimandare vera scienza, s’essa non passa per le matematiche dimostrazioni.
Chi baisima la somma certezza della matematica si pasce di confusione...
Molte volte una medesima cosa è tirata da due violenze: necessità e potenza. L’acqua piove, e la terra l’assorbisce per necessità d’omore; il sole la svelle non per necessità, ma per potenza.
Che cosa è la forza?
Forza dico essere una potenza spirituale [forza viva, manifestazione d’energia], incorporea, invisibile, la quale, con breve vita, si causa nei corpi, che per un’accidentale violenza si trovan fuori del loro essere e riposo naturale.
Forza dico essere una virtù spirituale, una potenza invisibile, la quale per accidentale esterna violenza è causata dal moto e collocata e infusa ne’ corpi, i quali sono dal loro naturale uso [la quiete] ritratti, dando a quelli vita attiva di maravigliosa potenza.
Ogni moto naturale e continuo desiderra conservare suo corso per le linia del suo principio...
Il moto è causa d’ogni vita. Ogni azione bisogna che si eserciti per moto.»

2. Giacomo Zabarella (1533-1589): è uno dei maggiori esponenti dell’aristotelismo padovano. Fra le sue posizioni va ricordata la distinzione fra «metodo compositivo» (sintesi) che deduce dalla conoscenza della causa quella dell’effetto e «metodo risolutivo» (analisi) che risale dalla esperienza dell’effetto alla conoscenza della causa: i due percorsi possono essere considerati rispettivamente come deduzione e induzione.
In ambito fisico egli rifiuta qualunque ipotesi di origine metafisica o teologica (ad es. le forze occulte neoplatoniche).
Inoltre bisogna ricordare che Aristotele, pur distinguendo scienze della natura e matematica, pensa che la matematica possa essere usata per spiegare fenomeni naturali, cioè per la ricerca delle cause.

Scrive, infatti, Galileo nel Dialogo sopra i due massimi sistemi: «Simplicio: [...] [si deve] concordare quel che ci porge l’esperienza con quel che ci dimostra Aristotile, perché chiara cosa è che due veri non si possono contrariare.
Salviati: [...] Aristotile non dic’egli che delle cose del cielo, mediante la gran lontananza, non se ne può molto resolutamente trattare? [...] non afferm’egli che l’esperienza e il senso si deve anteporre ad ogni discorso, ancorché ne paresse assai bene fondato? e questo non dic’egli resolutamente e senza punto titubare?
Simplicio: Dicelo [lo dice].» Dialogo, ed. Studio Tesi, p. 70

3. Tycho Brahe (1549-1601): anche se il suo sistema è un compromesso fra quello copernicano e quello aristotelico-tolemaico, è importante per il carattere strettamente osservativo dei suoi studi; infatti si rende conto osservando le comete che non esistono sfere celesti, ma orbite.

4. Johannes Kepler (1571-1630): è un matematico e astronomo che riceve per tutta la vita gli influssi del neoplatonismo. Infatti, nonostante le sue tre leggi sulle orbite elittiche, egli continua a proporre anche la corrispondenza fra i vari solidi platonici inscritti in sfere e le orbite dei pianeti del sistema solare.

«Kepler affermò che se la sfera di Saturno fosse circoscritta al cubo in cui risultasse inscritta la sfera di Giove e se [...], allora tutte le dimensioni relative di tutte le sfere risulterebbero esattamente quelle che Copernico aveva misurato. [...] Quest’uso che Kepler fa dei solidi regolari [platonici] non fu semplicemente una stravaganza giovanile, oppure, se lo fu, egli non diventò mai adulto. Una versione modificata della stessa legge apparve ternt’anni più tardi nelle “Armonie del mondo”, il libro che propone la terza legge.»
Thomas Kuhn, “La rivoluzione copernicana”, ed. it. Einaudi, p. 279-80.

Un giudizio simile, ma con contenuti errati, viene espresso da Galileo che non ammette l’attrazione gravitazionale della luna come causa delle maree, rifiutando come Zabarella ogni “forza occulta”. La spiegazione generale del fenomeno verrà data solo grazie a Newton e alla legge di gravitazione.

«Salviati: [...] Ma tra tutti gli uomini grandi che sopra al mirabile effetto di natura hanno filosofato, più mi meraviglio del Keplero che di altri, il quale, d’ingegno libero ed acuto, e che aveva in mano i moti attribuiti alla Terra, abbia poi dato orecchio ed assenso a predominii della Luna sopra l’acqua, ed a proprietà occulte, e simili fanciullezze.» Dialogo, ed. Studio Tesi, p. 584

5. Galileo Galilei (1564-1642) esalta il valore dell’osservazione (cannocchiale, crateri della luna, macchie solari...) e degli esperimenti, sia effettivi sia mentali: il valore del senso e delle necessarie dimostrazioni di tipo matematico (nei cui caratteri Dio ha “scritto” il “libro” del mondo).

Dialogo, cit., p. 182-83: «Salviati: Benissimo. Avete voi mai fatta l’esperienza della nave?
Simplicio: Non l’ho fatta; ma credo che gli autori che la producono l’abbiano diligentemente osservata [...]
Salviati: Io senza l’esperienza sono sicuro che l’effetto seguirà come vi dico, perché così è necessario che segua; [...]»