
In questo converter molti dei componenti che lo compongono si trovano in commercio racchiusi in un unico chip (controller) che è facilmente reperibile a basso costo. Se si fosse usato un controller al loro posto si sarebbe semplificato lo schema ed il circuito avrebbe avuto una dimensione più ridotta. Il fatto è che lo scopo principe dell'hobbista non è quello di costruire apparecchiature per venderle ma è quello di capirne il funzionamento, in effetti sarebbe impossibile indagare su tutti i punti dei componenti se essi fossero racchiusi in un integrato, in questo progetto, invece, ogni reoforo è libero di essere agganciato da una sonda dell'oscilloscopio o sondato con i puntali di un tester; tensioni, correnti e forme d'onda sono facilmente misurabili e visualizzabili in ogni punto del circuito attestando che questo progetto, con la sua apparentemente ingiustificata complessità, è nato per il solo uso didattico.
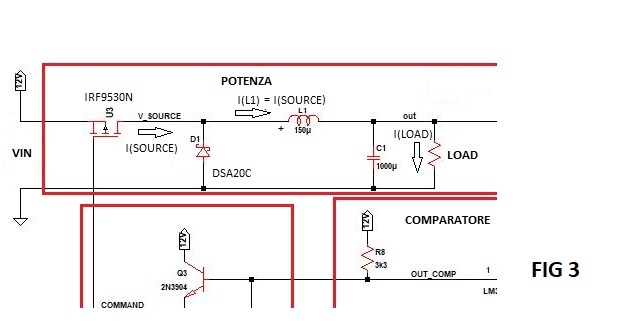
Lo schema del convertitore è rappresentato nella figura seguente.
Ho incorniciato i componenti creando dei blocchi ben definiti e distinti l'uno dall'altro per la funzione che svolgono.
Inizierò la descrizione del funzionamento in maniera oggettiva senza entrare in modo particolareggiato in ogni blocco che compone il convertitore. Seguirà poi un approfondimento di ogni parte del circuito e fornirò le equazioni necessarie per il suo dimensionamento. Per la spiegazione userò le forme d'onda fornite dal simulatore LTspice, sarebbe impossibile con un oscilloscopio a due canali poter osservare in un sol colpo tante forme d'onda tra loro correlate temporalmente, inoltre i segnali visualizzati dall'oscilloscopio sono sempre inficiati da disturbi e spike tipici dei circuiti prototipi, comunque ogni tanto fornirò alcune immagini di forme donde reali prelevate nei punti salienti del circuito.
Si analizzi la figura sottostante.
Premetto che lo studio, come in genere si fa, verrà eseguito sul sistema entrato a regime, tutti i transienti iniziali (che porteranno il sistema a regime) instauratesi subito dopo avere alimentato il circuito per ora non vengono considerati. Più avanti però, per pura curiosità, riporterò il loro andamento nel tempo.
Dato che il segnali in FIG 2 si ripetono periodicamente si può prendere qualsiasi punto temporale per iniziare l'analisi, scelgo, ad esempio, il punto A. Fintanto che il livello del segnale a dente di sega V(saw) è inferiore a quello di errore V(ve), ovvero tra i punti A e B l'uscita del comparatore rimane bassa. Questo ultimo segnale lo ritroviamo a circa lo stesso livello (dopo il buffer) sul gate del mosfet U3 che rimane in conduzione per il periodo di tempo tra A e B caricando l'induttore L1 con una corrente I(SOURCE) che cresce linearmente. Il diodo D1 è invece interdetto (I(SOURCE) = I(L1)).
La situazione è raffigurata nella seguente figura.
L'induttore si comporta come elemento passivo che assorbe energia, infatti il segno "+" è dalla parte dove entra la corrente.
Quando il livello del segnale V(saw) nel punto B supera quello del segnale V(ve) l'uscita del comparatore va alta e rimane in tale stato fino al tempo C, quindi il mosfet si interdice nel tempo che va da B a C (I(SOURCE) = 0). Dato che la corrente non può interrompersi istantaneamente la induttanza cerca di opporsi a questa nuova situazione invertendo la sua polarità come nella seguente figura.

Ora l'induttanza si comporta come un generatore rilasciando energia per tutto il tempo nel quale il mosfet è in interdizione, la corrente che circola in essa è quella che circola nel diodo D1 (I(L1) = I(D1)) ed ha andamento lineare decrescente.
L'onda della corrente I(L1) assume una forma triangolare e la corrente I(LOAD), circolante nel carico (costante grazie alla presenza del condensatore), si trova al centro di questo triangolo (vedi Fig. 2).
Suppongo ora che il carico subisca un incremento, allora la tensione ai suoi capi aumenta e di conseguenza aumenta la tensione presente al pin 6 di U2, essendo questo pin invertente la tensione errore V(ve) diminuisce, vediamo cosa succede tramite la seguente figura.
Essendosi abbassata la tensione V(ve) il periodo di tempo durante il quale il mosfet è in saturazione (da A a B) è diminuito rispetto alla precedente situazione. Questo significa che viene fornita meno energia alla induttanza e di conseguenza la tensione al carico diminuisce per tornare al valore nominale (o meglio, come vedremo, ad un valore molto vicino ad esso). Ovviamente quando il carico diminuisce la tensione V(ve) aumenta ed il periodo tra A e B aumenta fornendo più energia all'induttore con la conseguenza che la tensione al carico aumenta tornando ancora al suo valore nominale.
La spiegazione del convertitore fin qui data è solo illustrativa ed è stata esente da ogni relazione matematica, ora adrò più in profondità descrivendo ogni blocco in maniera approfondita e fornendo le relazioni matematiche per il dimensionamento dei componenti.
BLOCCO GENERATORE SEGNALE A DENTE DI SEGA

Si consideri la figura seguente.
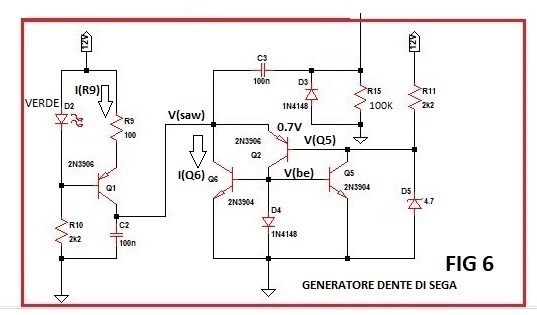
Il gruppo dei componenti D2, R9, Q1, R10 compone un limitatore di corrente che alimenta il condensatore C2, si analizzi la seguente figura.
Per partire con la spiegazione prendo un tempo nel quale il condensatore è scarico, ad esempio il punto A. Da qui il condensatore inizia a caricarsi, siccome esso è alimentato a corrente costante la tensione ai suoi capi cresce linearmente, quando raggiunge il valore di 5.4V ( la tensione del zener più 0.7V ai capi della giunzione B-E di Q2) Q2 entra in conduzione fornendo corrente al gruppo B-E di Q6, diodo D4, B-E di Q5 (ill diodo D4 serve per linearizzare la punta bassa del segnale a dente di sega).
Sia Q6 che Q5 entreranno in conduzione, Q6 scarica il condensatore (notare il picco di corrente I(Q6)) mentre Q5 tiene cortocircuitato il zener per permettere a Q2 di rimanere in conduzione per tutto il tempo della scarica (notare che il tempo nel quale Q6 e Q5 rimangono in conduzione è maggiore a quello necessario per la scarica del condensatore, questo è dovuto al ritardo dei transistor che ho usato io). Comunque il condensatore oltre a scaricarsi attraverso il collettore di Q6 si scarica anche attraverso Q2 e D4, questi tre componenti devono sopportare correnti impulsive dell'ordine dei 500mA ripetitivi. Si noti che la tensione del condensatore non va a zero ma si ferma a circa 0.2V, questo è dovuto alla tensione di saturazione di Q6.
Qui sotto la formula per dimensionare i componenti:
F = I(R9) / (C2 * delta_V)
dove:
F = frequenza dell'onda a dente di sega.
I(R9) = corrente costante.
C2 = condensatore.
delta_V = differenza tensione fine carica con tensione inizio carica.
Inizio a scegliere la frequenza, più è alta e più alte sono le perdite nell'induttore, nel mosfet e nel diodo D1 però più piccole sono le dimensioni dell'induttore e del condensatore di filtro C1, viceversa più è bassa e minori sono le perdite suddette ma risultano più grandi le dimensioni dell'induttore e della capacità. In genere le frequenza viene selezionata tra 25KHz e 50 KHz, nella scelta sono sceso ancora più in basso (20KHz) perché ho ritenuto che per questo convertitore non risultassero poi così grandi la capacità e l'induttore a quella frequenza.
Scelgo arbitrariamente un valore per il condensatore C2, 100nF.
La delta_V è la differenza tra il valore minimo e massimo del segnale:
delta_V = V(saw)_max -V(saw)_min = 5.4 - 0.2 = 5.2V
NOTA:
Come partenza introducete una tensione di saturazione generica di 0.2V, poi correggerete il valore di R9 (magari usando un trimmer al posto di una resistenza fissa) per regolare la frequenza al valore da voi prescelto.
Ricavo la corrente del limitatore.
I(R9) = F * C2 * delta_V = 20KHz * 100nF * 5.2 = 10mA
La formula per ricavare R9 è la seguente:
R9 = (V(D2) - 0.7) / I(R9) = (1.8 - 0.7) / 0.01 = 110 ohm
dove:
V(D2) è la caduta sul diodo led verde.
0.7 è la caduta sulla giunzione B - E di Q1.
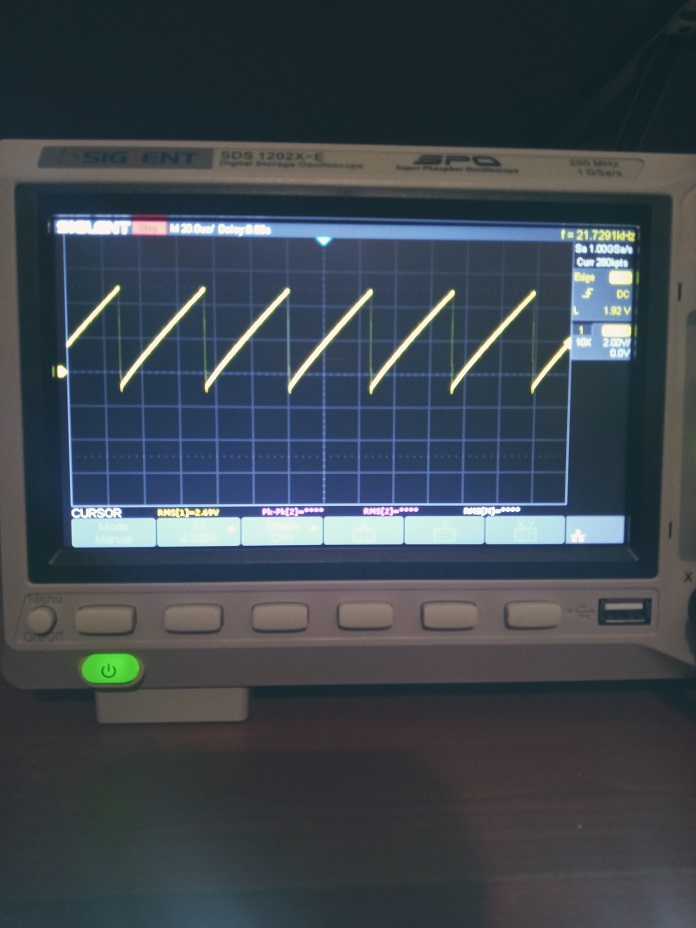
Con questo valore di componenti e con la loro tolleranza la frequenza misurata sul prototipo è di circa 21.7KHz. Si è visto che il livello più basso del segnale è di 0.2V, se si inviasse questo segnale al comparatore il convertitore non funzionerebbe perché appena fornitagli l'alimentazione il segnale errore V(ve) è a zero volt e per poter funzionare questo segnale deve salire al valore di regime e per farlo è necessario che il suo livello sia compreso in quello del segnale a dente di sega. Per ovviare a questo problema basta fissare quest'ultimo tramite il condensatore C3, il diodo D3 e la resistenza R15, il clamper per poter funzionare deve rispettare la seguente relazione:
R15 * C3 > 100*T
dove T è il periodo del segnale.
100K * 100nF > 100 * 50uS
0.01 > 0.005
La condizione è soddisfatta.
Nella figura sottostante si nota il segnale fissato (a circa -0.7V) nel circuito reale.
BLOCCO AMPLIFICATORE ERRORE

Con
questo circuito si può determinare la corrente di saturazione
dell'induttore. Il generatore di onda quadra deve avere la possibilità
di variare il duty-cycle del segnale generato. Tenete conto che quando
il livello del segnale è basso il mosfet conduce e quando è alto il
mosfet è interdetto. Quindi più è alto il duty cycle e per meno tempo il
mosfet è in saturazione.
Premetto
che l'amplificatore errore in questo progetto non è dotato di rete di
compensazione per non provare troppo la mia pazienza e quella del lettore
hobbista, comunque anche senza compensazione il sistema lavora bene
basta fare attenzione alla scelta del grado di amplificazione, esso non
può essere ne troppo basso ne troppo alto per i motivi che vedremo a
breve.
Qui sotto la parte del circuito riguardante l'amplificatore errore:
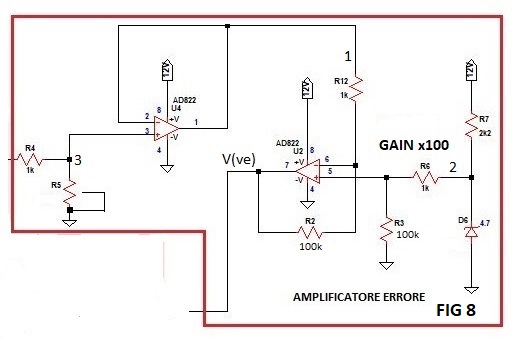
La tensione al carico si determina con la seguente formula approssimata:
V0 = V(source) * TON / T
dove:
V0 tensione al carico.
V(source) tensione sul catodo di D1 (con un carico di 1 ohm è pari a 10.43V, con un carico di 10 ohm è pari a 11.8V) quando il mosfet è chiuso (TON).
TON tempo nel quale il mosfet è chiuso.
T periodo del segnale.
Ipotizzo che il carico sia pari ad 1 ohm e regolo il trimmer R5 per avere 5V sul carico stesso (in realtà, data la criticità del trimmer, sono riuscito a regolare la tensione a 5.05V).
Ricavo il tempo TON
TON = T * V0 / VDC = 50uS * 5.05V / 10.43 V = 24.2uS
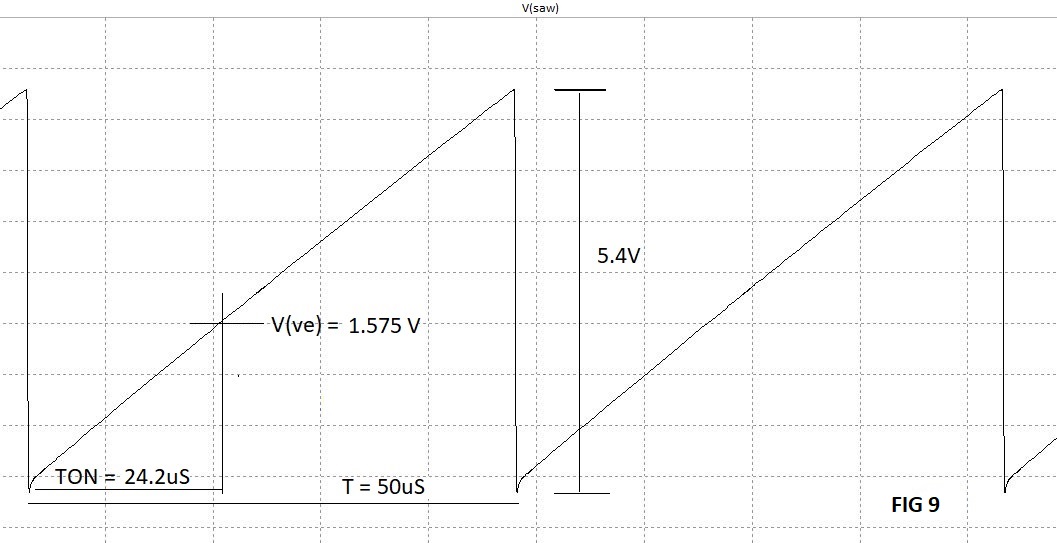
La tensione errore V(ve), l'ho misurata con il tester sul circuito, il suo valore è 1.575V, comunque essa può anche essere determinata graficamente (in maniera più approssimativa) in tal caso dovrete disegnare su carta millimetrata un triangolo con lato verticale alto 5.4 e quello orizzontale largo 50, scegliete una scala in grado di facilitarvi il compito della lettura, tracciate poi una verticale dal valore 24.2, il punto dove essa interseca la diagonale corrisponderà alla tensione errore V(ve).
Vedere figura successiva.
Tra i punti 1 e 2 c'è una differenza errore pari a (per il momento ipotizzo che l'amplificazione sia pari a 10 e non 100 come sul circuito):
VD = V(ve) / 10 = 1.575 / 10 = 0.1575V
Aumento il carico a 10 ohm, qui sotto i risultati ottenuti sempre con la stessa procedura.
V(ve) = 1.4022V
VD = 0.14022V
TON = 22.16uS
Aumentando il carico la corrente diminuisce e con essa le cadute nel mosfet e nell'induttore, la conseguenza è che la tensione al carico tende a salire ed il circuito di retroazione cerca di riportarla a al valore iniziale. Ma dato ora che la differenza di tensione VD è diminuita rispetto a quella che esisteva con il carico di 1 ohm la tensione al carico non è la stessa ma è leggermente diversa, vediamo perché.
Sul punto 1 (di conseguenza anche sul punto 3) c'è la seguente tensione:
V3 = VZ - VD = 4.58- 0,14022 = 4.56V
NOTA:
VZ misurata è 4.58V.
Quindi la tensione sul carico è:
V(load) = 4.56 * (R4 + R5) / R5 = 4.56 * 8100 / 7100 = 5.065V
Si nota che passando da un carico di 1 ohm ad un carico di 10 ohm la tensione aumenta di 15mV. Per sapere che effetto ha l'amplificazione su questa variazione di tensione ricalcolo il tutto con una amplificazione pari a 20.
Carico da 1 ohm:
V(load) = 5.07V
V(ve) = 1.57V
VD = 0.0785V
TON = 24.19uS
Carico da 10 ohm:
V(load) = 5.08V
V(ve) = 1.39V
VD = 0.0695V
TON = 22.15uS
Ora la differenza tra la tensione V(load) per un carico da 1 ohm ed un carico di 10 ohm è di 10 mV, ovvero è diminuita rispetto a quella con amplificazione pari a 10. Questo ci fa supporre che se l'amplificazione fosse infinita la tensione rimarrebbe costante per tutti i valori di carico, ovvero la tensione differenza sarebbe pari a zero, ma questo non è possibile prima perché non esistono amplificatori ad amplificazione infinita e poi perché il sistema può funzionare solo se esiste una, seppur piccola, tensione errore. Inoltre se si aumenta troppo l'amplificazione il sistema diviene instabile, nel mio prototipo sono arrivato ad una amplificazione di 100 e la variazione di tensione tra carico massimo e minimo è di solo qualche millivolt.
delta_I = (V(source) - V(load)) * TON / L1 = (11 - 5) * 24.2uS / 150uS = 0.968A (massima escursione del ripple)
I_max = I(load)_max + delta_I / 2 = 5 + 0.484 = 5.484A (picco superiore del ripple)
I_min = I(load) - delta_I / 2 = 5 - 0.484 = 4.51A (picco inferiore del ripple).
I(L1)_rms = sqrt(I(load)_max^2 + delta_I^2) = sqrt(25 + 0.93) = 5.01A (valore efficace della corrente, in questo caso molto vicina alla continua dato il piccolo valore di delta_I)
Bisogna scegliere un induttore da 150uH che possa sopportare una corrente efficace uguale o maggiore di 5A (sezione del filo) e presenti una corrente continua di saturazione maggiore di 5.484A (saturazione del nucleo magnetico).
La scelta potrebbe ricadere sull'induttore della Eaton, vedi figura sotto:

Se invece volete usare un induttore che avete in laboratorio del quale conoscete solo il valore della induttanza le seguente misura serve per determinare la corrente di saturazione.
Montate lo schema seguente:
Qui sotto la parte del circuito riguardante l'amplificatore errore:

La tensione al carico si determina con la seguente formula approssimata:
V0 = V(source) * TON / T
dove:
V0 tensione al carico.
V(source) tensione sul catodo di D1 (con un carico di 1 ohm è pari a 10.43V, con un carico di 10 ohm è pari a 11.8V) quando il mosfet è chiuso (TON).
TON tempo nel quale il mosfet è chiuso.
T periodo del segnale.
Ipotizzo che il carico sia pari ad 1 ohm e regolo il trimmer R5 per avere 5V sul carico stesso (in realtà, data la criticità del trimmer, sono riuscito a regolare la tensione a 5.05V).
Ricavo il tempo TON
TON = T * V0 / VDC = 50uS * 5.05V / 10.43 V = 24.2uS
La tensione errore V(ve), l'ho misurata con il tester sul circuito, il suo valore è 1.575V, comunque essa può anche essere determinata graficamente (in maniera più approssimativa) in tal caso dovrete disegnare su carta millimetrata un triangolo con lato verticale alto 5.4 e quello orizzontale largo 50, scegliete una scala in grado di facilitarvi il compito della lettura, tracciate poi una verticale dal valore 24.2, il punto dove essa interseca la diagonale corrisponderà alla tensione errore V(ve).
Vedere figura successiva.
Tra i punti 1 e 2 c'è una differenza errore pari a (per il momento ipotizzo che l'amplificazione sia pari a 10 e non 100 come sul circuito):
VD = V(ve) / 10 = 1.575 / 10 = 0.1575V
Aumento il carico a 10 ohm, qui sotto i risultati ottenuti sempre con la stessa procedura.
V(ve) = 1.4022V
VD = 0.14022V
TON = 22.16uS
Aumentando il carico la corrente diminuisce e con essa le cadute nel mosfet e nell'induttore, la conseguenza è che la tensione al carico tende a salire ed il circuito di retroazione cerca di riportarla a al valore iniziale. Ma dato ora che la differenza di tensione VD è diminuita rispetto a quella che esisteva con il carico di 1 ohm la tensione al carico non è la stessa ma è leggermente diversa, vediamo perché.
Sul punto 1 (di conseguenza anche sul punto 3) c'è la seguente tensione:
V3 = VZ - VD = 4.58- 0,14022 = 4.56V
NOTA:
VZ misurata è 4.58V.
Quindi la tensione sul carico è:
V(load) = 4.56 * (R4 + R5) / R5 = 4.56 * 8100 / 7100 = 5.065V
Si nota che passando da un carico di 1 ohm ad un carico di 10 ohm la tensione aumenta di 15mV. Per sapere che effetto ha l'amplificazione su questa variazione di tensione ricalcolo il tutto con una amplificazione pari a 20.
Carico da 1 ohm:
V(load) = 5.07V
V(ve) = 1.57V
VD = 0.0785V
TON = 24.19uS
Carico da 10 ohm:
V(load) = 5.08V
V(ve) = 1.39V
VD = 0.0695V
TON = 22.15uS
Ora la differenza tra la tensione V(load) per un carico da 1 ohm ed un carico di 10 ohm è di 10 mV, ovvero è diminuita rispetto a quella con amplificazione pari a 10. Questo ci fa supporre che se l'amplificazione fosse infinita la tensione rimarrebbe costante per tutti i valori di carico, ovvero la tensione differenza sarebbe pari a zero, ma questo non è possibile prima perché non esistono amplificatori ad amplificazione infinita e poi perché il sistema può funzionare solo se esiste una, seppur piccola, tensione errore. Inoltre se si aumenta troppo l'amplificazione il sistema diviene instabile, nel mio prototipo sono arrivato ad una amplificazione di 100 e la variazione di tensione tra carico massimo e minimo è di solo qualche millivolt.
BLOCCO POTENZA

Qui di seguito alcune formule che serviranno per scegliere l'induttore (fare riferimento alla precedente figura):
L'induttore
è il componente più critico di tutto il convertitore, con esso si
sceglie la corrente minima con la quale il convertitore ancora regola
efficacemente, inoltre l'induttore va scelto in modo che non entri mai
in saturazione al picco della corrente a carico più basso e che
possa sopportare il passaggio della corrente senza superare la sua
temperatura massima consentita.
Come già ho anticipato prima quando il mosfet è in saturazione l'induttore assorbe energia, dato che la tensione al carico si può ritenere costante grazie alla presenza del condensatore C1come pure quella sul drain del mosfet V(source), allora la corrente in L1 segue un andamento lineare crescente. Quando il mosfet si interdice l'energia dell'induttore si scarica sul carico e su C1, la corrente ora passa attraverso il diodo e segue un andamento lineare decrescente. Si tenga conto che quando il carico cambia varia l'ampiezza totale della corrente come nelle due figure sotto, la prima per un carico di 1 ohm la seconda per un carico di 5 ohm.
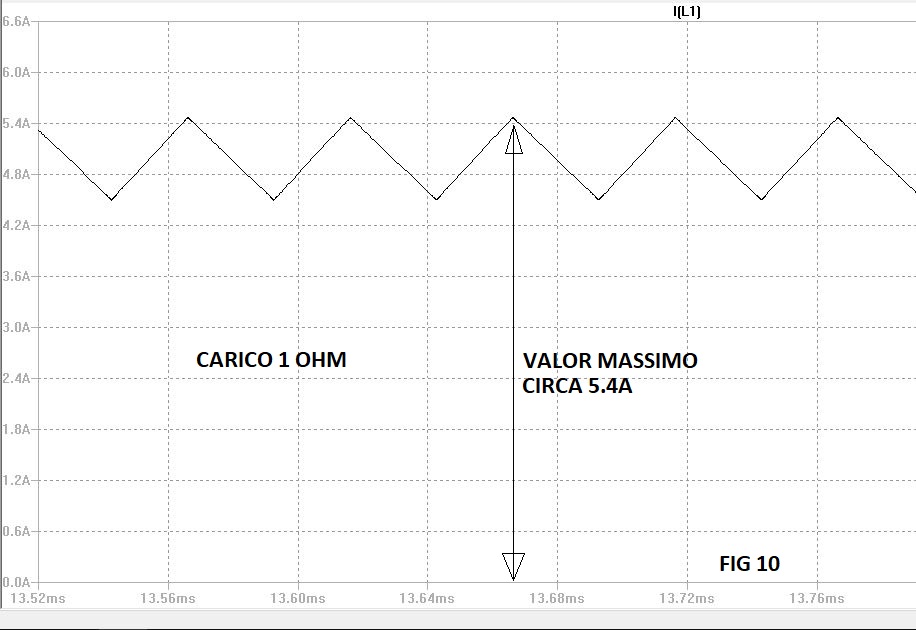
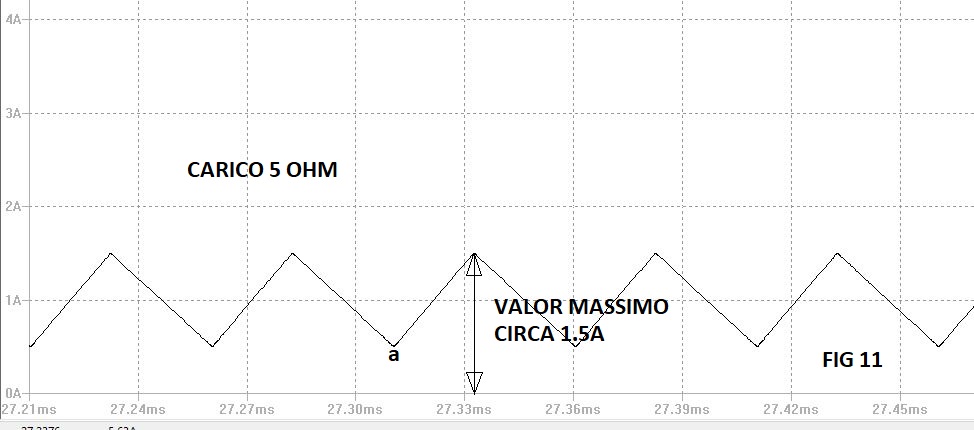
Si tenga conto che quando il carico si abbassa ulteriormente il punto "a" tocca l'asse dei tempi e l'induttore entra in "modo discontinuo". Il convertitore in questo stato ancora regola ma con meno efficienza. In genere si sceglie un valore minimo di corrente pari ad 1 / 10 del valore massimo.
I dati di partenza in un progetto di un buck converter sono i seguenti:
Tensione al carico V(load) = 5V
Tensione in ingresso VDC = 12V
Massima corrente assorbita dal carico I(load)_max = 5A (1 ohm)
Minima corrente assorbita dal carico I(load)_min = 0.5A pari ad 1 / 10 I(load)_max (10 ohm)
Formula per determinare l'induttanza (questa formula è valida solo per una corrente minima pari ad 1 / 10 della corrente massima che poi è uno standard del DC / DC buck converter)
L1 = 5 * (VDC - V(load) ) * V(load) * T / (VDC * I(load)_max ) = 5 * (12 - 5) * 5 * 50uS / (12 * 5) = 145.8uH (portato a 150uH)
Come già ho anticipato prima quando il mosfet è in saturazione l'induttore assorbe energia, dato che la tensione al carico si può ritenere costante grazie alla presenza del condensatore C1come pure quella sul drain del mosfet V(source), allora la corrente in L1 segue un andamento lineare crescente. Quando il mosfet si interdice l'energia dell'induttore si scarica sul carico e su C1, la corrente ora passa attraverso il diodo e segue un andamento lineare decrescente. Si tenga conto che quando il carico cambia varia l'ampiezza totale della corrente come nelle due figure sotto, la prima per un carico di 1 ohm la seconda per un carico di 5 ohm.
Si tenga conto che quando il carico si abbassa ulteriormente il punto "a" tocca l'asse dei tempi e l'induttore entra in "modo discontinuo". Il convertitore in questo stato ancora regola ma con meno efficienza. In genere si sceglie un valore minimo di corrente pari ad 1 / 10 del valore massimo.
I dati di partenza in un progetto di un buck converter sono i seguenti:
Tensione al carico V(load) = 5V
Tensione in ingresso VDC = 12V
Massima corrente assorbita dal carico I(load)_max = 5A (1 ohm)
Minima corrente assorbita dal carico I(load)_min = 0.5A pari ad 1 / 10 I(load)_max (10 ohm)
Formula per determinare l'induttanza (questa formula è valida solo per una corrente minima pari ad 1 / 10 della corrente massima che poi è uno standard del DC / DC buck converter)
L1 = 5 * (VDC - V(load) ) * V(load) * T / (VDC * I(load)_max ) = 5 * (12 - 5) * 5 * 50uS / (12 * 5) = 145.8uH (portato a 150uH)
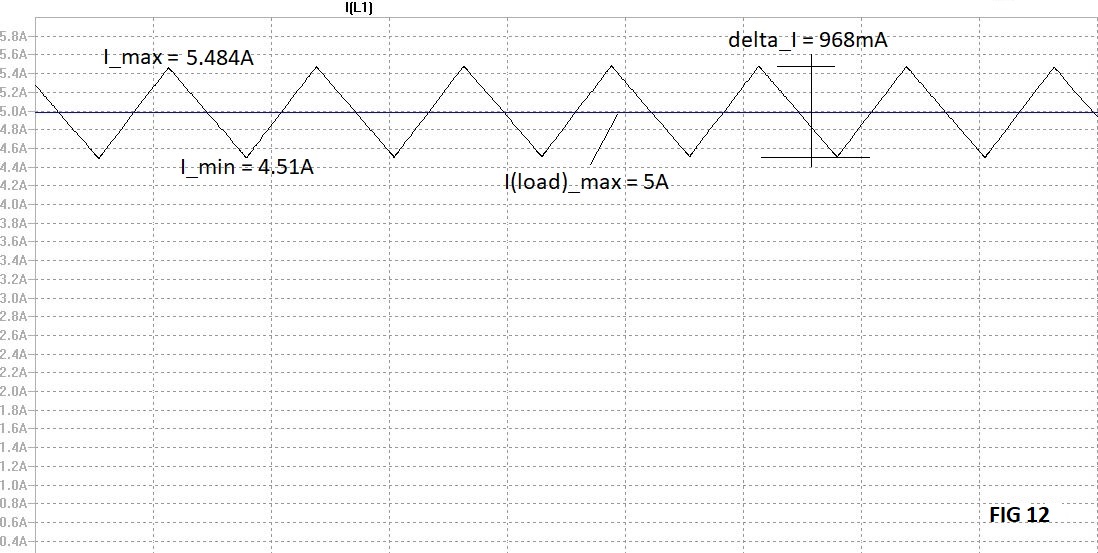
delta_I = (V(source) - V(load)) * TON / L1 = (11 - 5) * 24.2uS / 150uS = 0.968A (massima escursione del ripple)
I_max = I(load)_max + delta_I / 2 = 5 + 0.484 = 5.484A (picco superiore del ripple)
I_min = I(load) - delta_I / 2 = 5 - 0.484 = 4.51A (picco inferiore del ripple).
I(L1)_rms = sqrt(I(load)_max^2 + delta_I^2) = sqrt(25 + 0.93) = 5.01A (valore efficace della corrente, in questo caso molto vicina alla continua dato il piccolo valore di delta_I)
Bisogna scegliere un induttore da 150uH che possa sopportare una corrente efficace uguale o maggiore di 5A (sezione del filo) e presenti una corrente continua di saturazione maggiore di 5.484A (saturazione del nucleo magnetico).
La scelta potrebbe ricadere sull'induttore della Eaton, vedi figura sotto:
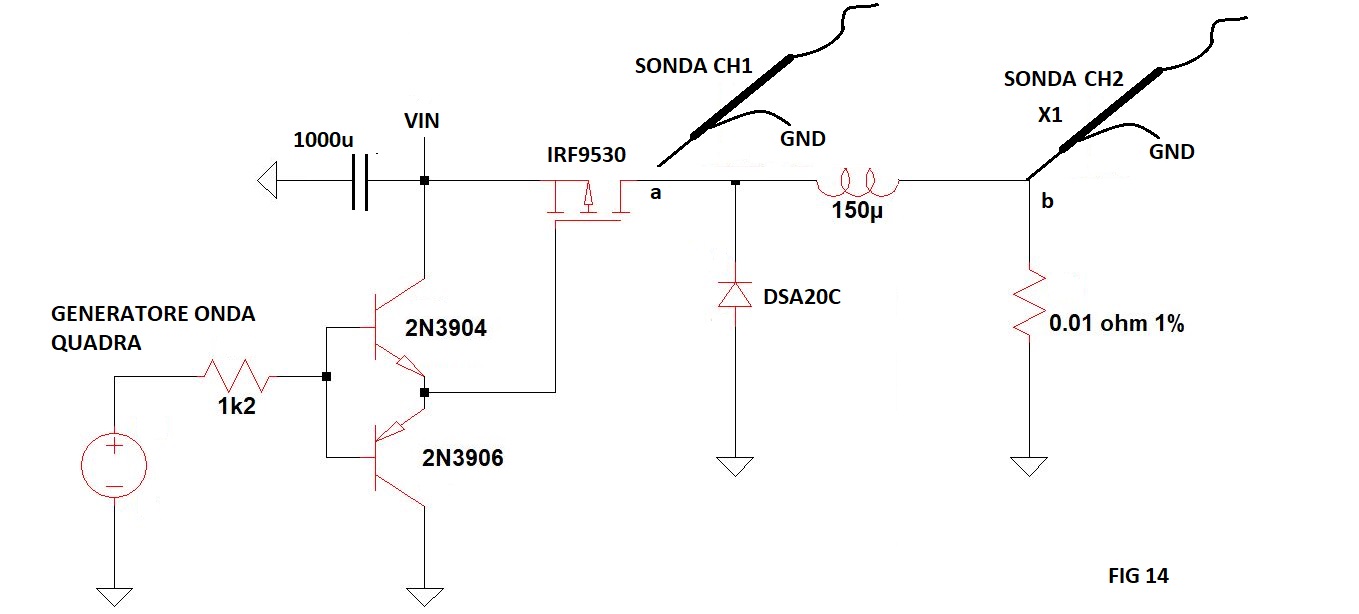
Se invece volete usare un induttore che avete in laboratorio del quale conoscete solo il valore della induttanza le seguente misura serve per determinare la corrente di saturazione.
Montate lo schema seguente:
Collegate la sonda del CH1 dell'oscilloscopio sul punto "a" (sonda X1 o X10 è indifferente), collegate la sonda del CH2 dell'oscilloscopio sul punto "b", questa deve essere X1 e il CH2 deve essere settato a X100 in modo che la lettura sulla resistenza sia diretta (quello che si legge è il vero valore di corrente che circola nella resistenza).
La tensione dell'alimentazione deve essere dello stesso valore di quella del segnale generato (io ho alimentato il circuito a 10V dato che il mio generatore può arrivare a quel livello).
Settate il duty-cycle più alto possibile (il mio generatore arriva 99.9%). Date alimentazione e osservate il CH2 dell'oscilloscopio. Vedrete la rampa di carica dell'induttore, scegliete una frequenza del segnale generato affinché quando il mosfet è in interdizione tutta l'energia dell'induttore venga trasferita alla resistenza (corrente pari a zero). A grandi valori del duty-cycle (tempi piccoli di saturazione del mosfet) la corrente circolante nell'induttore sale linermente come nella seguente figura.
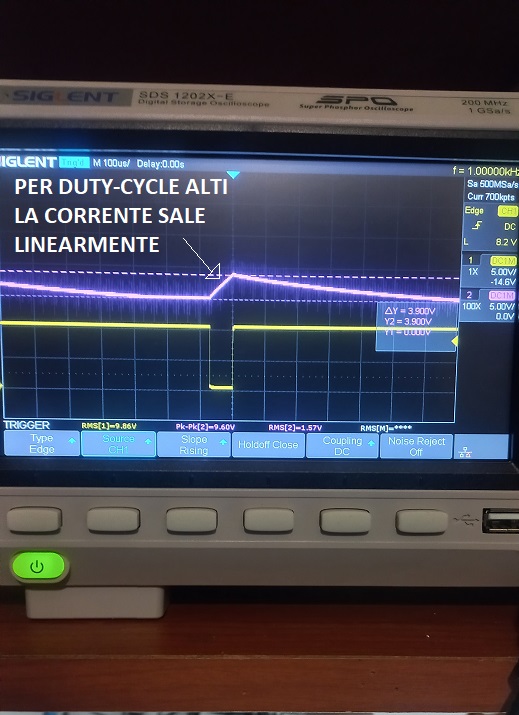
Diminuite il duty-cycle come nella seguente figura.
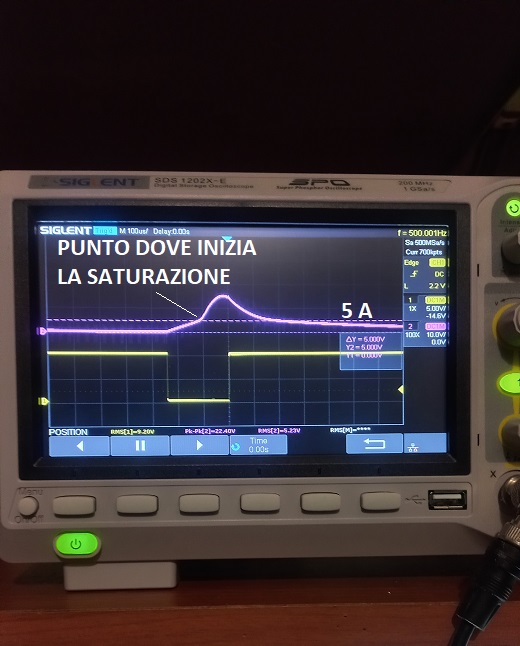
Leggete tramite cursori dell'oscilloscopio il valore in cui inizia la saturazione, nel mio caso 5A.
Per quanto riguarda la capacità del filo di sopportare una certa corrente rms basta imporre un valore piuttosto conservativo di 500 circular mil per rms ampere e misurare il diametro del filo, quello del mio induttore è 0.12 mm.
area filo = d / 2 * Pi^2 = 0.06 * Pi^2 = 0.59 mm^2
0.59 = 1164 circular mil (calcolatrice on line)
Irms = 1164 / 500 * 1 = 2.3A
Questo induttore non va bene per questo progetto a causa della basso valore di saturazione (in realtà lo provato per vedere l'effetto che poteva fare un induttore non idoneo, il risultato è stata bassa regolazione con il carico più basso).
Qui sotto il circuito prova.

Ho deciso allora di costruirne uno su toroide in polvere di ferro T80-26, con filo da 0.5 mmm di diametro, per avere 150uH occorrono 60 spire. I risultati sono i seguenti:
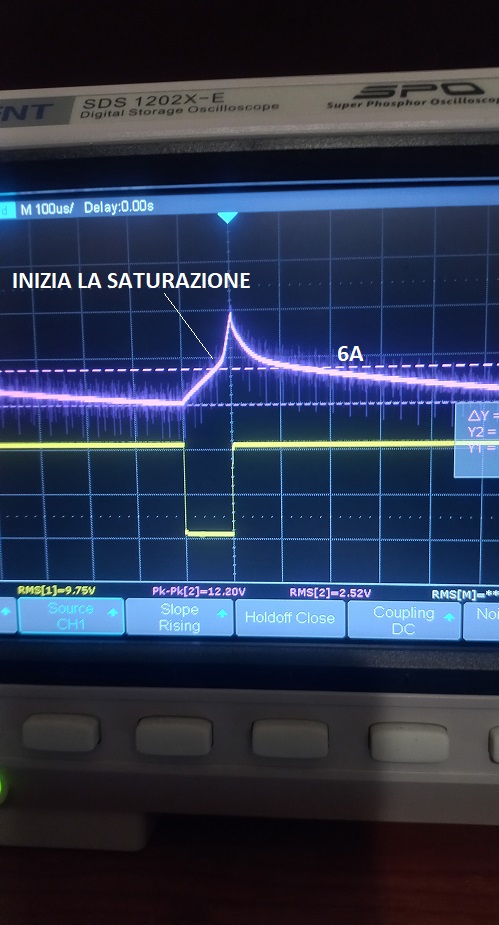
In questo induttore la saturazione inizia a 6A.
area filo = d / 2 * Pi^2 = 0.06 * Pi^2 = 2.46 mm^2
2.46 = 4855 circular mil (calcolatrice on line)
Irms = 4855 / 500 * 1 = 9A
Questo induttore potrebbe andare bene.

In realtà la misura con NanoVna mi ha dato un valore di induttanza inferiore di 150uH ma dal punto di vista del funzionamento non cambia molto. Vedi figura seguente:

A regime l'induttore si scalda fino a 83 °C (da TA = 14 °C), Questo è dovuto prevalentemente al passaggio della corrente (5A) nel filo elettrico dato che la corrente alternata dovuta al ripple è piccola (circa 300mVRMS) e di conseguenza lo è la perdita nel nucleo del toroide.

Per poter verificare questa asserzione ho alimentato l'induttore con un alimentatore con corrente limitata a 5A ed il risultato è stato che la massima temperatura raggiunta è stata di 83°C (da TA = 14°C) la stessa di quando era montato nel circuito. Vedi la seguente figura.

Quindi la potenza dissipata è:
PL1 = 4.99 * 1.2 = 5.98 W
Tenendo conto che i nuclei a polvere di ferro dopo 80 °C iniziano a perdere le loro caratteristiche e per il fatto che questa potenza persa in calore abbassa il rendimento del convertitore (che è importantissimo per i DC-DC) questo induttore ancora non va bene per questo progetto. Ho provato quindi un altro induttore che mi permettesse di usare un filo più spesso.
Ho trovato nel cassetto una barretta di ferrite di quelle che si usano per ricevere le stazioni AM, siccome era molto lunga l'ho tagliata. Per tagliarla bisogna stare molto attenti dato che la ferrite è un materiale che si rompe molto facilmente. L'ho tenuta bloccata nella morsa (senza stringerla troppo) e ho tagliato la barretta con un taglia tubi. Bisogna avere molta pazienza e stringere il taglia tubi molto poco ad ogni giro. Vedi figura sotto.

Ho avvolto 75 spire sulla barretta per ottenere 150 uH, ho usato un filo di diametro pari a 1mm e poi ho eseguito le stesse precedenti misure ottenendo una potenza dissipata di:
PL1 = 5 * 1= 5 W
minore di quella di prima, vedi figura sotto:

La temperatura ora sale solo a 30°C (da TA = 15 °C), uno perché il diametro del filo è più grande e poi perché l'avvolgimento è più esposto all'aria rispetto a quando era avvolto sul toroide e si raffredda meglio.
Per pura curiosità ho voluto abbassare ulteriormente la potenza dissipata nel filo usando un toroide in povere di ferro T184-26 che permette agevolmente di usare un filo di 1.5 mm di diametro, 30 spire danno un un valore di induttanza pari a 150 uH.
Vedi figura sotto.

Per determinare la corrente di saturazione ho usato lo stesso circuito di fig. 14 ed il risultato è visualizzato sotto.
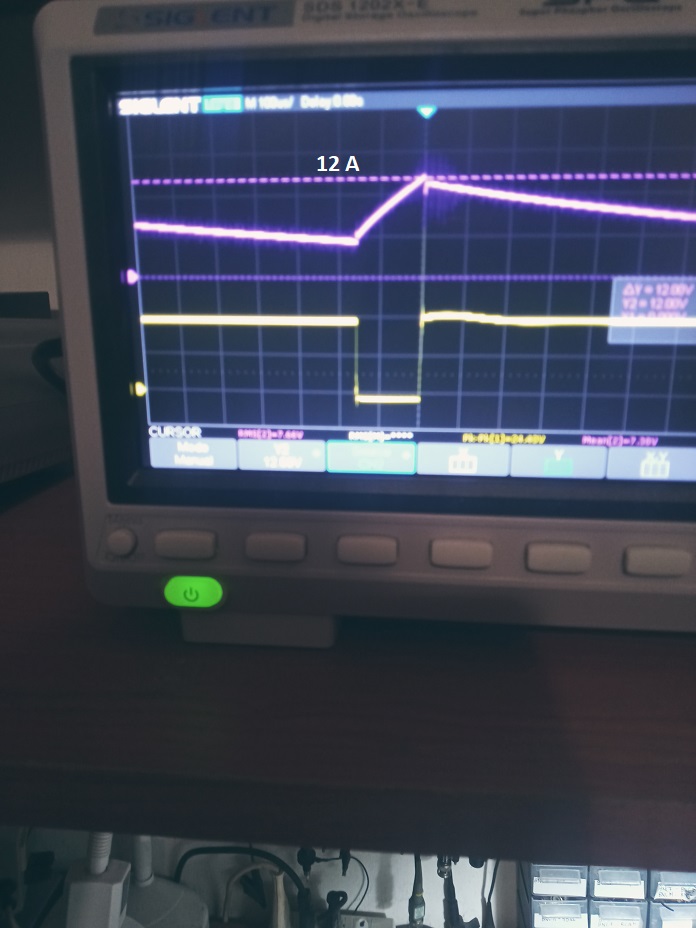
La rampa di corrente è lineare fino a 12A (non ho potuto provare valori superiori a 12 A perché il mio alimentatore non può erogarli, inoltre nella prova il mosfet si scalda e la sua corrente di drain è dichiarata essere 12 A a 25 °C e decresce con l'aumentare della temperatura. Per questo la prova deve durare pochissimo, fatta la lettura, a quei livelli di corrente, occorre rialzare immediatamente il duty-cycle o togliere l'alimentazione).
Nella figura sotto si vede la dissipazione su questo induttore.
La potenza dissipata nell'induttore è ora:
PL1 = 5 * 0.5 = 2.5 W
Ovvero si è dimezzata.
Vedi figura sotto.

Per determinare la capcità C1 si applichi la seguente formula:
C1 = 65 * 10^(-6) * 0.2 * I(load)_max / Vrr = 65 * 10 ^(-6) * 0.2 * 5 / 0.07 = 958 uF (uso 1000 uF)
dove:
65 * 10 ^(-6) è l'ESR del condensatore (valore che mediamente si riscontra negli elettrolitici)
I(load)_max è la corrente con il carico più basso (1 ohm)
Vrr è il ripple desiderato (ho scelto 0.07V).
In parallelo al condensatore elettrolitico occorre metterne uno di 10nF (che ha un ESR più basso alle alte frequenze) per attenuare il ripple ulteriormente (dell'ordine del 50% al 60%).
Nella seguente figura la tensione sul carico di 1 ohm.

Il mosfet deve sopportare una corrente maggiore di I_max = 5.484A e almeno una tensione doppia di VCC, deve inoltre presentare una bassa resistenza di chiusura per minimizzare le perdite quando è in saturazione.
Il gate del mosfet assorbe corrente ogni qual volta c'è un brusco cambiamento di livello da alto a basso e viceversa, in genere, per la maggior parte dei mosfet utilizzati per queste potenze, questa corrente si aggira intorno ai 200mA, dato che il comparatore LM339 non è in grado di fornirla occorre mettere un buffer a BJT tra il comparatore ed il gate del mosfet.
RENDIMENTO
Con l'utilizzo del primo induttore il rendimento a pieno carico è:
rend = (P_load / P_alim) * 100 = (4.99 * 5.13) / (3.15 * 12) * 100 = 67.7 %
Vedi figura sotto.

Con il secondo induttore:
rend = (P_load / P_alim) * 100 = (5.09 * 5) / (2.80* 12.1) * 100 = 75.1 %
Aumentato notevolmente.
Vedi figura sotto:
.
Con il terzo induttore:
rend = (P_load / P_alim) * 100 = (5.18 * 4.99) / (2.73 * 12) * 100 = 79 %
Aumentato ancora.
Vedi figura sotto:

Fabio
rend = (P_load / P_alim) * 100 = (4.99 * 5.13) / (3.15 * 12) * 100 = 67.7 %
Vedi figura sotto.

Con il secondo induttore:
rend = (P_load / P_alim) * 100 = (5.09 * 5) / (2.80* 12.1) * 100 = 75.1 %
Aumentato notevolmente.
Vedi figura sotto:
.

Con il terzo induttore:
rend = (P_load / P_alim) * 100 = (5.18 * 4.99) / (2.73 * 12) * 100 = 79 %
Aumentato ancora.
Vedi figura sotto:

Fabio